Раздел: Документация
0 ... 6 7 8 9 10 11 12 ... 39 г ОБОБЩЕНИЕ ГЛАВЫ 1.Компьютеры оперируют числами, представленными в двоичной системе счисления. Это связано с тем, что в электронных устройствах и устройствах памяти проще всего реализуются системы с двумя устойчивыми состояниями. 2.Для представления отрицательных чисел используют двоичное число со знаком (представление в дополнительном коде). 3.Шестнадцатеричная система применяется для «сжатия» данных, то есть для более экономичной записи чисел. Она позволяет в четыре раза уменьшить число разрядов по сравнению с двоичной системой. 4.В компьютере при выполнении действий с числами могут использоваться четыре основные логические операции - логическое сложение (ИЛИ), логическое умножение (И), отрицание (НЕ) и (Исключающее ИЛИ). Практические задания 1)Объясните, каким образом с помощью электрических или магнитных устройств можно представить цифры двоичного числа «О» и «1». 2)Переведите в десятичную форму двоичное число со знаком «10011101»- 3)АЛУ процессора производит лишь операцию сложения двоичных чисел. Объясните, каким образом выполняется вычитание. 4)Вспомните, в каких случаях в программе, составленной для микрокомпьютера, могут использоваться логические операции. 4  Микрокомпьютер конструируется на основе цифровых схем. В свою очередь, цифровая схема состоит из различных электронных компонентов: сопротивлений, конденсаторов, диодов, транзисторов и т. д. На Рис. 4.1 показаны так называемые «дискретные» (то есть выполненные в виде отдельных деталей) электронные компоненты. Соединенные между собой определенном образом, они представляют собой электронные устройства, реализующие различные логические функции. На печатной плате современного компьютера вы не увидите большого количества дискретных компонентов, так как основная часть элементов, составляющих его схему, находится внутри интегральных схем (ИС). В корпусе одной ИС размещается огромное количество электронных элементов, сформированных на одном кристалле. Исключение составляют так называемые «гибридные» ИС, содержащие некоторое количество миниатюрных бескорпусных дискретных компонентов. В зависимости от количества элементов, сформированных на одном кристалле, интегральные схемы делятся на схемы малой, средней, высокой и сверхвысокой степени интеграции. 1.К схемам малой степени интеграции, или малым интегральным схемам (МИС, SSI), относятся ИС, в которых число элементов не превышает 100. 2.Схемы средней степени интеграции (СИС, MSI) содержат от 100 до 1000 элементов. Итак, мы познакомились с основными свойствами четырех логических операций: логическое сложение «ИЛИ», логическое умножение «И», отрицание «НЕ» и «Исключающее ИЛИ», рассмотрели примеры их использования. Микрокомпьютеру часто приходится выполнять логические операции при выполнении определенных команд, смысл и назначение которых мы объясним позже. Эти команды часто используются в операциях над разрядами двоичных чисел. Они служат для того, чтобы устанавливать, сбрасывать или инвертировать значения в требуемых разрядах двоичных чисел. г 4. Цифровые схемы = = 4. Цифровые схемы -ллл- Резистор 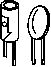 <ZI) Конденсатор Й- Диод  Сток 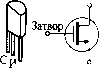 я-р-яр-и-р Биполярные 3Исток Полевой транзистор транзисторы Основные компоненты электронных схем Рис. 4.1. Обозначения и внешний вид основных компонентов электронных схем 3.Схемы большой степени интеграции - большие интегральные схемы (БИС, LSI) - содержат от 1000 до 10000 элементов. 4.Класс интегральных схем сверхвысокой интеграции (СБИС, VLSI) составляют ИС с числом элементов больше 10000. В зависимости от полупроводниковой технологии, используемой при их изготовлении (биполярные или полевые транзисторы), различают транзисторно-транзисторные логические схемы (ТТЛ) и схемы на комплиментарных МОП-транзисторах ( КМОП). Кроме того, имеются варианты ТТЛ и КМОП интегральных схем с усовершенствованными характеристиками. Например, разработаны маломощные ТТЛ-схемы на диодах Шоттки (ТТЛШ) с потреблением тока в 4 раза меньше, чем у стандартных ТТЛ. На Рис. 4.2 показано, как внешне выглядят интегральные схемы некоторых типов. В интегральной схеме множество элементов сформировано на одном кристалле Кремниевая подложка (кристалл размером несколько мм) ИС, изготовленные по различным технологиям  И С на биполярных транзисторах  ИС на КМОП-транзисторах ИС различной степени интеграции МИС Меньше 100 элементов 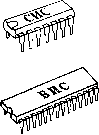 От 100 до 1000 элементов Больше 1000 элементов Рис. 4.2. Виды интегральных схем Прочитав вторую главу, мы узнали, что процессор и запоминающее устройство микрокомпьютера являются большими интегральными схемами. Порты ввода-вывода обычно также выполнены на больших интегральных схемах. Кроме того, интегральные схемы различных типов используются для передачи сигналов и данных Между процессором, ЗУ и портами ввода-вывода. Для того чтобы разобраться в работе микрокомпьютера, мы должны изучить функции интегральных схем, из которых он построен. Мы также должны иметь представление о цифровых схемах, с помощью которых осуществляется взаимодействие портов ввода-вывода с внешними Устройствами. Рассмотрению этих вопросов и посвящена настоящая глава. г 4. Цифровые схемы = 4.1. Вентильные схемы 4.1. ВЕНТИЛЬНЫЕ СХЕМЫ Вентильными, или комбинационными, схемами называют электронные устройства, выполняющие те самые логические операции, которые мы изучили в предыдущей главе: логическое сложение «ИЛИ», логическое умножение «И», отрицание «НЕ», «Исключающее ИЛИ». Существуют стандарты обозначения логических элементов на схемах в зависимости от выполняемых ими функций. В Табл. 4.1 представлены обозначения электронных элементов, реализующих перечисленные выше логические функции. Таблица 4.1. Логические элементы, выполняющие четыре основные операции
Любую логическую функцию можно реализовать с помощью комбинации, состоящей из вентильных схем четырех типов, соответствующих четырем основным логическим операциям. Довольно часто (прежде всего в силу технологических причин) применяются логические элементы, выполняющие операции «ИЛИ-НЕ» и «И-НЕ». Функции и обозначения таких логических элементов представлены в Табл. 4.2. Таблица 4.2. Логические элементы, выполняющие операции «И-НЕ» и «ИЛИ-НЕ»
ИЛИ НЕ ИЛИ-НЕ И НЕ И-НЕ Все четыре основные логические функции можно реализовать с помощью одной и той же схемы «И-НЕ», которая посредством дополнительных инвертирующих каскадов легко преобразуется в другие типы вентильных схем (Рис. 4.3). ~[ Применение вентилей «И-НЕ» С Схема «НЕТ)( Схема «И») 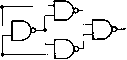 (Схема «ИЛИ») (Схема «Исключающее ИЛИ») С помощью вентилей «И-НЕ» можно реализовать любую логическую функцию Оказывается, из вентилей И-НЕ» можно собрать любую югическую схему.  Рис. 4.3. Варианты реализации основных вентильных схем посредством логических элементов «И-НЕ» 0 ... 6 7 8 9 10 11 12 ... 39 |












