Вы находитесь в разделе Типовых решений систем безопасности

Эллиптические кривые: новый этап развития современной криптографии

В недавно начавшемся XXI веке системы телекоммуникации и обработки цифровой информации играют все более и более значительную роль в различных видах деятельности человека. Они уже сейчас исключительно важны для нормального существования целых государств. В указанных условиях проблема защиты телекоммуникационных систем и систем обработки информации от внешних воздействий, имеющих целью внести искажения в их работу, приобретает не просто важное, а критическое значение - от нее зависит безопасность и само выживание людей.

Два направления в криптографии

Одним из ключевых инструментов защиты информационных систем является криптография. Ее сущность заключается в использовании преобразований информации, доступных законным сторонам информационного цикла и недоступных всем остальным. В отличие от множественных других подходов стойкость криптографических методов защиты может быть надежно обоснована, а в отдельных случаях и формально доказана теоретико-информационными методами. В настоящее время в криптографии принято выделять два крупных направления: классическую (одноключевую, симметричную) и современную (двухключевую, асимметричную) криптографию. Первая возникла в глубокой древности, ее исходной целью было обеспечение секретности переписки. В рамках данного подхода все законные участники цикла идентичны по своим возможностям - любые действия, доступные одному из них, доступны и остальным, поскольку все они разделяют единственный секрет. Очевидно, использование этих методов защиты предполагает взаимное доверие сторон. Классическая криптография решает весьма узкий круг задач, среди которых обеспечение секретности данных при их хранении или передаче по каналам связи и защита от навязывания ложных данных.

Первое достигается путем шифрования данных, а второе - за счет добавления к данным имитовставки. Использование методов классической криптографии порождает вторичные проблемы защиты, такие как потребность в защищенном канале связи для передачи секретных ключей корреспондентам. Узость круга решаемых задач и потребность в надежном канале распределения ключей, безусловно, являются ограничениями классического подхода в криптографии. Но он также обладает и неоспоримыми преимуществами: высоким быстродействием и высокой стойкостью при относительно небольшом размере ключей. По этим показателям классическая криптография на порядки превосходит современную и по указанной причине продолжает широко использоваться как самостоятельно, так и в составе гибридных схем защиты. Второе направление - так называемая современная криптография - возникла уже в наше время, в середине семидесятых годов прошлого века. Она ориентирована на решение иных, более современных задач, перед которыми классическая криптография оказалась бессильной. Протоколы асимметричной криптографии незаменимы в ситуациях отсутствия взаимного доверия м. сторонами. Каноническими, исходными задачами "современной" криптографии являются: двухключевое шифрование, распределение секретных ключей по несекретным каналам связи и подпись цифровых документов (хотя в рамках данного подхода решается гораздо более широкий круг задач).

Тенденции развития и проблемы современной криптографии

Алгоритмы традиционной криптографии строятся путем комбинирования большого числа относительно несложных преобразований способом, обеспечивающим хорошие характеристики итогового алгоритма. Практические основы были заложены в работах Хорста Файстеля [1], и с тех пор принципы построения одноключевых шифров изменились не весьма сильно. Помимо некоторого расширения набора базовых преобразований и большего разнообразия в архитектурах изменения носят в основном количественный характер и отражают развитие используемой вычислительной базы. Важно, что типовой размер ключей и блоков данных, применение которых считается безопасным, вырос примерно в 2 раза. Иная картина наблюдается в современной криптографии. Стойкость ее алгоритмов базируется на недоказанной пока вычислительной невозможности эффективного решения некоторых математических задач, значит на гипотезе, которая может оказаться ошибочной. Например, стойкость криптосистемы RSA [2, 3] базируется на сложности задачи факторизации больших чисел, а стойкость современных схем ЭЦП, большинство из которых являются вариациями обобщенной схемы Эль-Гамаля, - на сложности задачи логарифмирования в конечных полях. В настоящее время в современной криптографии существуют следующие проблемы:

1. Ограниченность числа рабочих схем. В отличие от алгоритмов классической криптографии, которые могут быть созданы в неограниченном количестве путем комбинирования различных элементарных преобразований, каждая "современная" схема базируется на определенной "нерешаемой" задаче. Как следствие, количество рабочих схем криптографии с открытым ключом весьма невелико.
2. Постоянная "инфляция" размера блоков данных и ключей, обусловленная прогрессом математики и вычислительной техники. Так, если в момент создания криптосистемы RSA считался достаточным размер чисел в 512 бит, то сейчас рек. не менее 4 Кбит. Иными словами, "безопасный" размер чисел в RSA вырос практически на порядок; похожая картина наблюдается и для других схем, как в традиционной криптографии этот размер увеличился всего вдвое.
3. Потенциальная ненадежность базиса. В настоящее время теорией вычислительной сложности исследуется вопрос о возможности решения задач данного типа за полиномиальное время (гипотеза Р = NP). В рамках теории уже доказана связь большинства используемых вычислительно сложных задач с другими аналогичными задачами. Это означает, что, если будет взломана хотя бы одна современная криптосистема, многие другие также не устоят.
4. Отсутствие дальней перспективы. Уже известен предполагаемый "могильщик" современной криптографии - это квантовыевычисления, с помощью которых оказалось возможным решать многие задачи гораздо быстрее, чем на традиционных компьютерах. Правда, в настоящее время они существуют лишь в теории, из практических достижений можно отметить только успешную факторизацию числа 15 "микромакетом" квантового вычислителя [4]. Специалисты полагают, что "многозначительные" квантовые компьютеры появятся примерно через 25-30 лет, и за пределами этого срока будущее современной криптографии туманно. Из всего вышесказанного следует, что для современной криптографии актуальна проблема повышения стойкости и уменьшения размера блоков данных путем модификации уже существующих криптосистем.

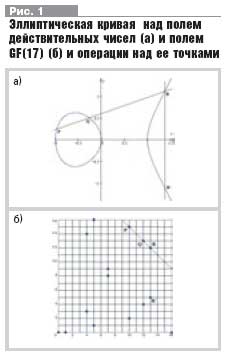
Основные понятия эллиптических кривых

Самый очевидный путь решения вышеупомянутой проблемы - представление блоков информации в криптографических алгоритмах не только в виде чисел (или элементов конечных полей), но и в виде иных алгебраических объектов большей сложности. Одним из весьма подходящих типов таких объектов являются точки эллиптических кривых. Первоначально эллиптической кривой называлась гладкая кривая на Декартовой плоскости, описываемая следующим уравнением:

у²+а₁ху+а₃у=х³+а₂х²+а₄х+а₆ (1)

Если все коэффициенты и неизвестные - действительные числа, то путем замены переменных уравнение (1) может быть преобразовано к следующему, более простому виду:

у²=х³+ах+b. (2)

Уравнение (1) может рассматриваться над произвольными полями, и в частности, над конечными полями, представляющими для криптографии особый интерес. В последнем случае решением уравнения (1) является множество отдельных точек, а не линия, но и в этом случае по традиции пишут об эллиптических кривых. В качестве примера на рис. 1 (а, б) приведена эллиптическая кривая у²=х³-х над полем действительных чисел и полем вычетов по модулю GF(17) соответственно.

Эллиптические кривые используются в криптографии с середины 80-х г. прошлого века в качестве инструмента решения некоторых теоретико-числовых задач и в качестве основы для построения криптосистем. Любая кривая над полем действительных чисел, задаваемая уравнением общего вида (1), обладает следующими св, в формулировке которых условимся точку касания считать за два пересечения:

i. Любая вертикальная (параллельная оси Оу) прямая, не пересекает кривую ни разу или пересекает ее дважды.

ii. Любая другая прямая пересекает кривую один или три раза.

Добавим к множеству точек эллиптической кривой фиктивный элемент "О" (называемый обычно "бесконечной точкой"), который будет играть роль нулевого элемента конструируемой аддитивной группы: для любой точки Р эллиптической кривой положим Р + О = О + + Р = Р. Операции отрицания и сложения определяем чтобы для каждой прямой, пересекающей эллиптическую кривую дважды или трижды, "сумма" всех точек пересечения с учетом их кратности при касании была "равна нулю":

R + R' = O - для вертикальных прямых,

P + Q+R = O - для невертикальных прямых (см. рис. 1).

Первое соотношение определяет правило отрицания - аддитивным обратным элементом для любой точки R эллиптической кривой является другая точка пересечения кривой и вертикальной прямой: R' = -R. Второе соотношение определяет правило сложения точек: суммой двух точек кривой является отрицание третьей точки пересечения кривой и прямой, проведенной через первые две: Р + Q = -R = = R' (см. рис. 1). Для определенных аддитивных операций выполняются все требования к операциям в абелевых группах:

1. Операция сложения точек очевидным образом коммутативна: для любых точек Р, Q эллиптической кривой справедливо Р + Q = Q + Р.
2. В проективной геометрии доказывается ассоциативность операции сложения точек: для любых трех точек Р, Q, R эллиптической кривой справедливо (Р + Q) + R = P + (Q+R).

множество точек эллиптической кривой с добавленной к нему бесконечной точкой О и определенными указанным выше способом операциями отрицания и сложения точек образуют аддитивную абелеву группу, элементы которой могут использоваться в качестве "заменителей" обычных чисел.

Эллиптические кривые над конечными полями

Определенные выше операции над точками кривых могут быть распространены на случай произвольного поля. Необходимые формулы могут быть получены, если воспользоваться алгебраическими выражениями для геометрических понятий - "прямая", "вертикальная прямая", "касательная".

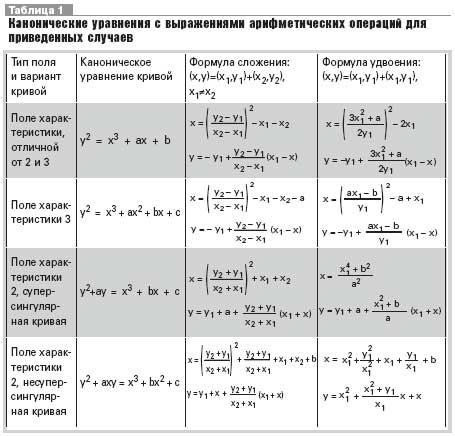
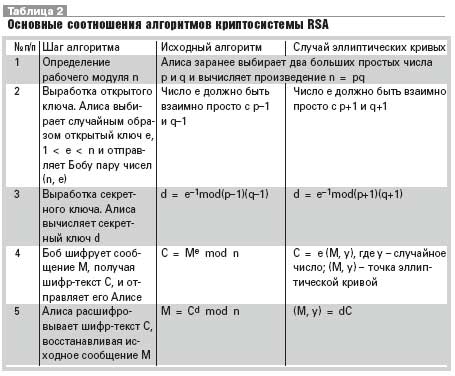
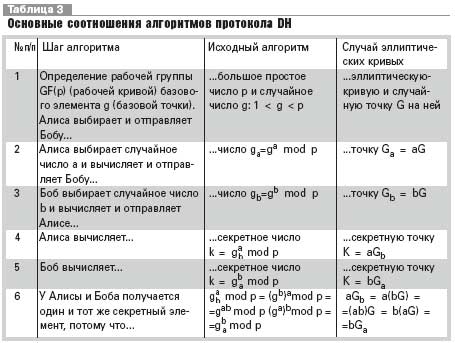
Следует указать, что не для всякого конечного поля уравнение кривой может быть приведено к виду (2). Так, для конечного поля характеристики 3 невозможно избавиться от члена а₂х², если а₂ отлично от нуля. Для полей характеристики 2 уравнение (1) может быть приведено к одному из следующих видов:

у2+ау=х3+Ьх+с (3) (суперсингулярная кривая);

у²+аху=х³+bх²+с (4) (несуперсингулярная кривая).

Заметим, если степень поля есть нечетное число, то заменой переменных можно добиться того, что коэффициенты в уравнении (3) будут равны либо 0, либо 1. В табл. 1 приведены канонические уравнения для каждого из указанных случаев вместе с выражениями арифметических операций над точками. Для криптографии особую важность представляет нахождение кратного точки эллиптической кривой: Q = кР, где к - большое натуральное число. Эта операция аналогична возведению элемента конечного поля в большую натуральную степень и выполняется по точно такой же схеме.

Криптографические схемы на эллиптических кривых

Большинство криптосистем современной криптографии естественным образом можно "переложить" на эллиптические кривые. Ниже мы изучим варианты некоторых наиболее распространенных криптосистем. Во всех описаниях Алиса и Боб считаются законными участниками информационного цикла. Криптосистема RSA - шифрование с открытым ключом и ЭЦП В табл. 2 приведены основные соотношения алгоритмов криптосистемы RSA. В варианте RSA на эллиптических кривых используется кривая у² = х³ + b с условием p = q = 5(mod 6) или кривая у² = x³ + ax с условием p = q = 3(mod 4). В обоих случаях эллиптическая кривая анализируется не над конечным полем, а над кольцом вычетов по составному модулю п. Параметры b и а соответственно не задаются пользователем, а "стихийно складываются" при выборе Бобом (отправителем сообщения) случайного числа у. Для операций с точками кривой знать параметр b нет необходимости, а параметр а легко находится с помощью расширенного алгоритма Евклида по заданной точке (х, у) из уравнения y² = x³ + ax.

Отметим, что стойкость криптосистемы RSA в обоих случаях базируется на сложности разложения числа п на множители, поэтому она и похожие системы, базирующиеся на сложности факторизации, в варианте на эллиптических кривых не имеют преимуществ перед своими оригиналами. В то же самое время у них есть недостатки, например удвоенный размер шифр-текста. По указанной причине криптосистемы данного типа в варианте на эллиптических кривых не нашли сколь-нибудь значительного практического применения.

Протокол (открытого распределения ключей) DH

Протокол DH - это выработка двумя сторонами общего секретного ключа путем обмена информацией по открытому каналу связи. В табл. 3 приведены основные соотношения алгоритмов протокола DH. Для определения секретного элемента противнику необходимо решить задачу Диффи-Хеллмана для мультипликативной группы конечного поля GF(p) либо для группы точек эллиптической кривой, значит определить gab, зная д, да и gb, но не зная а и Ь. Эта задача сводится к задаче дискретного логарифмирования, значит определения х по известным g и дх. Для групп точек некоторых эллиптических кривых эта задача является гораздо более трудной, чем для "обычных" полей GF(p) и GF(2^m). Наиболее эффективным методом логарифмирования в них является алгоритм обобщенного решета числового поля, как для группы точек эллиптической кривой наилучшая эффективность логарифмирования обеспечивается при использовании г- и 1-методов Полларда, существенно более трудоемких. Следует отметить, что переход на эллиптические кривые не приводит к автоматическому возрастанию стойкости криптосистем. есть проблема надлежащего выбора параметров эллиптической кривой. Например, для суперсингулярных кривых над полем GF(2^m) задача логарифмирования сводится к аналогичной задаче для исходных конечных полей с возможным возрастанием размерности в 2-4 раза. Для несуперсингулярных кривых есть другая проблема: при выборе кривой необходимо обеспечить высокий порядок группы точек эллиптической кривой. По указанным причинам для применения в криптографии рек. использовать только несуперсингулярные кривые над полем GF(2^m) либо кривые над полем GF(p). Во всех случаях необходимо убедиться, что порядок соответствующей группы достаточно большой и в этой группе есть элементы большого порядка.

Старый и новый стандарты ЭЦП РФ -ГОСТ34.10-94/01

В табл. 4 приведены основные соотношения для старого и нового стандартов ЭЦП РФ.

Из представленных в табл. 4 данных очевидна полная аналогия старого и нового стандартов ЭЦП РФ. Различия заключаются в том, что в старом стандарте некоторые операции выполнялись в конечном поле GF(p), а в новом - в группе точек эллиптической кривой над полем GF(p).

Выводы

практически любая "современная" криптосистема может быть "переложена" на эллиптические кривые, но не для всех схем это дает выигрыш в стойкости. Например, для системы RSA и родственных ей систем, основанных на сложности задачи факторизации, это не усиливает схему. В то же время для схем, основанных на сложности задачи логарифмирования в дискретных полях, переход на эллиптические кривые позволяет существенно увеличить стойкость. Обусловлено это тем, что при надлежащем выборе параметров кривой задача логарифмирования в группе точек кривой существенно сложнее задачи логарифмирования в мультипликативной группе исходного поля. Этот факт в сочетании с быстрой "инфляцией" схем "современной" криптографии привел к повсеместному переходу на эллиптические кривые в "чувствительных" областях применения. Так, старые стандарты ЭЦП РФ и США, просуществовав около 7 лет, с 1994 по 2001 гг., практически одновременно были заменены новыми, реализующими прежние криптографические схемы на эллиптических кривых, что позволило существенно увеличить стойкость и сократить размер блоков данных. Старый российский стандарт оперировал 1024-битовыми блоками данных, новый оперирует 256-битовыми. При этом, по оценкам специалистов, трудоемкость взлома старого и нового стандартов ЭЦП России составляет величину порядка 1026 и 1038 операций умножения в базовом поле GF(p) соответственно. По указанной причине в настоящее время происходит массовый перевод асимметричных криптосистем, основанных на сложности задачи логарифмирования в дискретных полях, на эллиптические кривые.

Литература

1. Feistel H. Cryptography and Computer Privacy, Scientific American, May 1973, Vol. 228, №. 5, p. 15-23
2. Menezes A., Van Oorschot P., Vanstone S. Handbook of applied cryptography. CRC Press, 1997.
3. Schneier B. Applied Cryptography. Protocols, algorithms and source code in c//John Wiley & sons, inc., 1996. (Русский перевод: Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си // М.: "Триумф", 2002.)
4. Lieven M.K. et al. Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. - Nature 414. 20-27 Dec. 2001.

Э.А. Применко,
доцент МГУ им. Ломоносова

А.Ю. Винокуров
главный эксперт ММВБ

Читайте далее:
Что день грядущий нам готовит
Эллиптические кривые: новый этап развития современной криптографии
Глобальная интеграция
Хранители древностей
Интеграция инженерных систем в единой системе контроля и управления зданием "Magic House"
Какую систему выбрать для охраны нетелефонизированных объектов
Крепость на колесах
Антитеррористическое оборудование: состояние и перспективы
Метрологическое обеспечение радиоконтрольного оборудования
Негосударственная охрана и безопасность в Российской Федерации
Новые авиационные технологии ликвидации последствий чрезвычайных ситуаций
Нормативно-техническая база для создания и развития единых дежурно-диспетчерских служб субъектов Рос