Раздел: Документация
0 ... 40 41 42 43 44 45 46 ... 82 если выполняются равенства А3=А\, S3=Bi, А4=А2 и В4 = В2, то W2(p) = = — Wi(p) = B2/Bi Таким образом, чтобы передаточные функции для напряжений Ui и U2 операционного преобразователя по схеме рис 6-1, а различались только знаками, достаточно взять попарно одинаковыми четырехполюсники ЧП1 и 4773, 4П2 и 4774 Во многих случаях желаемые передаточные функции можно получить, применяя на входах ОУ и в обратной связи не четырехполюсники, а пассивные двухполюсники Можно считать в данном случае, что двухполюсник — это частный случай четырехполюсника, для которого А~\, B-—Z, С=0, d=l, где z — операторный индекс двухполюсника (операторное сопротивление между входом и выходом двухполюсника) Соответственно передаточные функции операционного преобразователя при применении двухполюсников на входе и в обратной связи ОУ будут следующими: (7»=---; wtiP)=-b- \+z;?;. (б-з) Примеры операционных преобразователей. Рис 6-2, а показывает схему операционного преобразователя, обеспечивающего получение двойного интеграла от входных напряжений U\ и U2 При этом используются Т-образные ЯС-четырехполюсники, схемы которых показаны на рис. 6-2, б и е. Нетрудно убедиться, что для первого из этих четырехполюсников (рис 6-2, б) A = l+pC1R1; В = /?!+ Ri + pC1R1R2, а для второго (рис 6-2, в) 1 . в 1 , 1 .1 4 = 14- - : в = —.— л--.—и -■ . pC2R3рС2 рС, p2C2CaR, Соответственно, используя формулу (6-2), можем записать ХГг (р) = t/вых (Р) РС2 pCs p*C2CsR3 UiiP)Ri + Rt + pCiRiR, 1 1+P(C, + C,) Rd p*c2Cs(ri + R,)ri ~1+рС11Я2/(Я1+Й2) Если обеспечить равенство постоянных времени (C2+C3)i?3 = Cl/?iR2: : (r1+r2), то передаточная функция будет соответствовать двойному интегрированию: W1 (р) =--!-. В частном случае, когда Ct = C, С2 = Сз = С/2, R3=R, Ri=R2=2R, получим Г.(р)=-1/(С«/г«) Как было показано выше, для того чтобы получить W2(p)=—Wi(p). где W2(p) — передаточная функция для напряжения 1)% достаточно взять попарно одинаковыми четырехполюсники, присоединенные к И- и Н-входами ОУ. В данном случае, чтобы получить Ш2(р) — \/(ргС2Я2), нужно принять Ct = C, С5 = С6=С/2, R6 = R, rt = Rs**2R На рис 6-3 показаны примеры схем дифференцирующего звена и инерционного звена первого порядка Для схемы рис 6-3, а если /?i = 0, то W(p)=—pCR2, т. е. получаем функцию преобразования дифференцирующего звена (/вых(г) =—dUBx(t)/dt В практических схемах дифференцирующих преобразователей, как правило, последовательно с входным конденсатором включают резистор небольшого сопротивления (R1 на рис 6-3, а) Этот резистор, во-первых, уменьшает высокочастотные шумы на выходе (при идеальном дифференцировании коэффициент усиления преобразователя растет пропорционально частоте входного сигнала, так что для высокочастотных входных шумов усиление больше, чем для низкочастотных) Во-вторых, этот резистор способствует предотвращению высокочастотных автоколебаний (цепь обратной связи дифференцирующею преобразователя вносит фазогый сдвиг, снижающий устойчивость) Наконец, l третьих, резистор R1 ограничивает ток и напряжение И-входа ОУ при рез- R1 R2С2„ C3UR1 R2 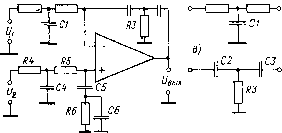 Рис 6-2 Схема операционного преобразователя, выполняющего двойное интегрирование (а), и схемы используемых в нем четырехполюсников (б и в) ких изменениях входного напряжения, когда выходное напряжение ОУ не успевает измениться соответствующим образом из-за ограниченной скорости нарастания Вполне понятно, что резистор R1 ограничивает полосу рабочих частот дифференцирующего преобразователя Преобразователь дифференцирует вход- 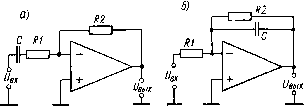 Рис. 6-3 Схемы, моделирующие дифференцирующее звено (а) и инерционное звено первого порядка (б) ные сигналы только тех частот, при которых сопротивление конденсатора С много больше сопротивления резистора R1, т е при/<С\/(2nRiC). Передаточная функция преобразователя по схеме рис. 6-3, б соответствует инерционному звену первого порядка w(p)~ ——!-. Ri рС/?2 + 1 Подобный преобразователь применяется в тех случаях, когда нужно усилить постоянную составляющую входного сигнала и сгладить содержащиеся в этом сигнале пульсации В частности, если на вход такого преобразователя подать одинаковые импульсы стабильной вольт-секундной площади, то постоянная составляющая напряжения на выходе преобразователя будет Пропорциональна средней частоте этих импульсов. Именно так нередко строят частотные демодуляторы. Пример применения ОУ в фильтре нижних частот иллюстрирован рис. 6-4, а. Пульсации выходного сигнала через разделительный конденсатор С2 и резистор R2 попадают на И-вход 5) ОУ. Выход ОУ соединен конденсатором Ct с выходом фильтра. Резистор R3 ста-билизирует режим работы ОУ по постоянному току. Если предположить, что в рассматриваемой области частот сопротивление конденсатора С2 много меньше сопротивления резистора R2, то граф, соответствующий схеме рис. 6-4, а м.ожно изобразить так, как показано на рис. 6-4, б. На основании этого графа получаем 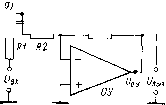 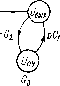 Рис 6-4. Схема простейшего активного фильтра нижних частот (а) и ее граф (б) GiG3 R, Ubhx (Р) UBX (р) G3 (G12 + pCj) 4- Gjpd"~ Rl + Rt pCiRiR2 Ri + Rz 1 + R* Из этого соотношения видно, что за счет применения ОУ достигнут эффект увеличения постоянной времени фильтра в 1 +R3/R2 раз. Достоинством этого фильтра является его быстрый выход на рабочий участок [7]. При большом скачке напряжения Ubx (например, при включении напряжения) ОУ входит в насыщение, и тогда конденсатор С1 заряжается при Ri>Ri с постоянной времени R\C\. Затем, когда ОУ выходит на линейный участок, постоянная времени фильтра возрастает в I+R3/R2 раз. 6-2. Интегрирующие операционные преобразователи Особенно большое применение находят в измерительной технике и технике аналогового моделирования интегрирующие операционные преобразователи — интеграторы. Простейший интегратор, применяемый наиболе часто, строится так, как показано на рис. 6-5, а. Этот интегратор имеет передаточную функцию W(p) = —1 /(р/? 1 Сг), которая говорит о том, что выходное напряжение будет равно интегралу по времени от входного напряжения, взятого с обратным знаком, причем постоянная интегрирования равна R\C\. Идеальное интегрирование, однако, было бы возможно только в случае применения в интегрирующем преобразователе идеального ОУ. Если же учесть конечное значение коэффициента усиления К ОУ и его входное сопротивление гвх, то на основании графа рис. 6-5,6 получим Ujmxip) К1(\ 4- Kl/Увх) W(P): UBX (Р) Ri Ri + rB (6-4) 0 ... 40 41 42 43 44 45 46 ... 82 |












