Раздел: Документация
0 ... 43 44 45 46 47 48 49 ... 82 Н-вход ОУ Передаточная функция интегратора для низких частот в этом случае приобретает вид vv---, ртх (К+1)4-1-+1) где рп — коэффициент положительной обратной связи. Если установить /Срп=1, т. е. $П=1/К, то получим W(p) = l/(pti). Интегратор может быть построен путем включения конденсатора на место нагрузки любого из рассмотренных выше пре- R1R2R1R2 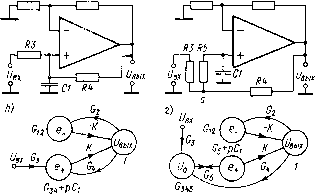 Рис 6-9. Схемы интеграторов с заземленным конденсатором ("а и б) и их графы (б н г) образователей напряжения в ток. В частности, находит применение интегратор на основе усилителя с цепями ООС и ПОС, показанный на рис. 6-9, а. В этом интеграторе конденсатор имеет один заземленный зажим, что облегчает введение в интегратор заданных начальных условий. Исходя из графа рис. 6-9,6, для этого преобразователя находим передаточную функцию в виде W (р) = ~г--■ 5><G,4 + pd) + KG, <6М + pCj) - к<чОп Выбирая резисторы таким образом, чтобы обеспечить равенство G12G34 + KGtG3i - KGtGlt = О,(6-11) получим передаточную функцию, характерную для интегратора, W(p) =-*C,G"—.(6-12) V рС!(612+ KG2)у Если теперь из (6-11) выразить 012 и подставить в (6-12), то для преобразователя по схеме рис. 6-9,а окончательно найдем 1 + /?«//?» W(p)- pCiR3 Можно предложить еще одну разновидность неинвертирую-щего интегратора, схема которого и соответствующий граф показаны на рис. 6-9, в и г. Передаточная функция этого преобразователя, найденная из графа, будет следующей: W (р) = GsG,K0l2 ------ Gi2G345 (°5 + pCj) + kg% [аиъ (g5 + pej - Gi] - ор12-а,о5ко12 Выполним условие G12G345G5 + KG2 (G345G5-G2)-G\GX2-GfibKGn = 0. (6-13) Тогда получим передаточную функцию, характерную для интегратора, W(p)= КО0з°5 . . ,(6-14) pC(Gu KG2) Преобразуя (6-14) с учетом (6-13), получим окончательно W(p) =-1 + Ri/R*-. (6-15) РСг (Я, + R5 + R3Rb/Rd В интеграторе по схеме рис. 6-9, в имеется возможность получения больших постоянных времени интегрирования при относительно небольших сопротивлениях и емкости, входящих в устройство. Действительно, как следует из (6-15), постоянная времени в данном случае равна shrT- ГТГг Это вы- ражение означает, что увеличение постоянной времени может быть получено при увеличении отношения R5/R4. 6-3. Активные фильтры Активные фильтры на основе ОУ находят широкое применение в измерительной аппаратуре Синтез активных фильтров состоит из нескольких этапов Аппроксимация амплитудно-частотной характеристики является основрй первого этапа синтеза. Активный фильтр обычно представляет собой линейною цепь, состоящую нз конденсаторов, резисторов н операционных усилителей. Его передаточная характеристика описывается отношением двух полиномов, содержащих различные степени оператора р. В частности, передаточная характеристика фильтра нижних частот (ФНЧ) имеет вид j j G (р) =-=---,(6.16) 1 + 4- . . . + апрп-х + апрп где Н — номинальный коэффициент передачи фильтра в полосе пропускания, п — порядок фильтра. Квадрат амплитудно-частотной характеристики (АЧХ) для ФНЧ соответственно будет представлять собой дробь следующего вида [(7(ш) р = .--.-—Ё1-! . (6.17) 1 + 6[W2+ . . . т.Чб/" Задача аппроксимации в данном случае состоит в выборе порядка и коэффициентов полинома, стоящею в знаменателе этой формулы. Характеристика идеального ФНЧ показана штриховой линией на рис 6-10. Идеальный фильтр пропускает с одинаковым коэффициентом (равным, например, единице) колебания, частота которых лежит в диапазоне от 0 до некоторой частоты среза wc. Вне этого частотного диапазона идеальный фильтр имеет коэффициент передачи, равный нулю. При выборе полинома, входящего в (6-17), стремятся достичь наилучшего в том или ином смысле приближения 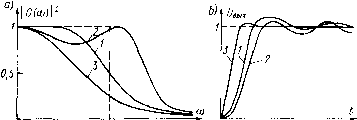 О(осО Рис 6-10 Амплитудно-частотные (а) и переходные (б) характеристики раяличных фильтров нижних частот реальной характеристики фильтра к идеальной Причем, чем выше порядок полинома, тем больше будет приближаться реальный фильтр к идеальному, но тем сложнее будет его реализация Известны и широко применяются тр1 вида активных фильтров, отличающиеся друг от друга подходами к нахождению наилучшей аппроксимации. Это фильтры Баттерворта, Чебышева и Бесселя В фильтре Баттерворта аппроксимирующая функция ищется как функция, для которой ее значение и значения ее производных в точке w = 0 совпадают с соответствующими значениями идеальной функции Для идеального фильтра очевидно, что при w = 0 G(w)2=l, а все производные G (со) по со в этой точке равны нулю Если проанализировать аппроксимирующую функцию (6-16), то нетрудно показать, чтб наилучшее в указанном смысле приближение к идеальной характеристике мы получим, придавая функции (6-17) следующий вид: I G (со) « = . 1 + 6„ш2 (6-18) Действительно, все производные по частоте до (2га—1)-й включительно от функции (6-18) в точке w = 0 равны нулю Сама же функция в этой точке равна постоянной величине Н2, отличие которой от единицы в общем случае не имеет значения Формула (6-18) описывает в общем виде АЧХ фильтра Баттерворта. Изменяя входящий в (6-18) коэффициент Ьп, мы имеем возможность изменять частоту среза ФНЧ. При теоретическом анализе часто принимают Н=\ и 0 ... 43 44 45 46 47 48 49 ... 82 |












