Раздел: Документация
0 ... 42 43 44 45 46 47 48 ... 82 как бы размыкается и переходный процесс будет в этом случае определяться постоянной времени ту, а не Т\!К. Многовходовый интегратор. На основе рассмотренного интегратора можно в соответствии с общей схемой рис. 6-1, а построить многовходовый интегратор, позволяющий получать алгебраическую сумму интегралов нескольких входных напряжений (рис. 6-7, а). Передаточная функция этого преобразователя для напряжения иг, поданного на И-вход ОУ через резистор Rx, будет та- 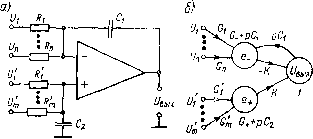 Рнс 6 7 Схема многовходового интегратора (а) и ее граф (б) кои же, как у рассмотренного выше одновходового интегратора: №,(р)=--~-—. pdRt (K+l) + Rfi- Для напряжения (У/, поданного на Н-вход через резистор R/, соответственно получим (см. граф на рис. 6-7,6) G]K(b + pC1) (G + РСг) (G+ + РС2) 4 КрС1 G i (рт + 1) 0+ [рт (К + 1) + 1] (рт+ + 1) /де G =G!+... + G„; G+= G/+ ... 4- Gn; t = Ci/G ; t+=C2/G+. Из последнего выражения для W}(p) следует, что для получения интеграла напряжения (У/ нужно обеспечить равенство постоянных времени т- и т+. Если принять Ci = C2, то условием получения интеграла со стороны Н-входа будет равенство G+=G . Можно рекомендовать следующий порядок проектирования многовходового интегратора. Пусть необходимо обеспечить получение выходного напряжения, изображение которого по Лапласу имеет вид PTiРЧ pTj Выбираем С1 = С2 = С. Находим сопротивления входных резисторов Ri = ti/C, R/ = x//C. Определяем суммарные проводимости пт G = С 2(1/т() и G+ = С 2 (1/т/)-Если получаем, что GG+, то И- или Н-вход ОУ соединяем с землей дополнительным резистором так, чтобы достичь равенства G =G+. Если в интеграторе по схеме рис. 6-7, а не выдержано условие равенства постоянных времени т+ = т-, то в его выходном напряжении кроме интеграла входных сигналов будут присутствовать еще составляющие, соответствующие реакции много-входового инерционного звена, присоединенного к Н-входу ОУ, на входные сигналы Ui-i-Um. Целесообразно иметь в виду, что можно построить много-входбвый интегратор на основе рассмотренного выше простей- 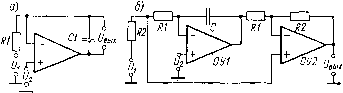 Рис 6-8 Варианты схем интегралов шего интегратора рис. 6-5, а, если снимать выходное напряжение с конденсатора обратной связи. На рис. 6-8, а показан подобный вычитающий интегратор. Если считать ОУ идеальным, то выходное напряжение этого интегратора, как нетрудно убедиться, будет определяться равенством BbIX(P) = -L-l(P)-l(P)]- р*1 Достоинством интегратора по схеме рис. 6-8, а является малое число элементов, и, кроме того, здесь не требуется выполнения дополнительных условий для получения передаточной функции интегратора. Его недостаток —• незаземленный выход. Естественным методом перехода от незаземленного к заземленному выходу является применение дифференциального усилителя. Простейший такой усилитель (рие. 6-8, б) дает интеграл лишь для U2: /7ВЬ1Х (р)=[/7, (p)~U2(p)]R2/[pCRl (Rl+R2)] + Ul (р). Если в интеграторе по схеме рис. 6-8, а или б требуется иметь число входов, большее двух, то это нетрудно сделать. Входные напряжения в этом случае на И-вход ОУ (рис. 6-8, а) подаются через соответствующие резисторы точно так, как напряжение Ui подается через резистор R1 Что касается Н-входа ОУ, то если требуется подвести к нему несколько входных напряжений, все они также должны быту поданы через соответствующие резисторы (тем самым мы образуем резистив-ный сумматор). Подобным образом можно увеличить число входов и в интеграторе по схеме рис. 6-8,6, Интеграторы по схеме рис. 6-8 находят применение и тогда, когда требуется интегрировать только один входной сигнал. В частности, целесообразность такого применения может определяться требованием высокого входного сопротивления, которое здесь обеспечивается для источника U2. Кроме того, переход от интегратора рис. 6-5, а к интегратору рис. 6-8, а приводит к снижению погрешностей интегрирования на высоких частотах [46]. Найдем, например, передаточную функцию интегратора по схеме рис. 6-8, а для входного напряжения U\. Для этого вначале, пользуясь графом рис. 6-5, в, определим напряжение е- (р) = UBX (р) —- C1(pTy + i)(gBb,x + Pc1)-= (°г + РСг) CTy +- 1) (gBbIX + рСу) + KgBUXpC1 - Р2С2 х Х(рту+ 1) = UBX (р)-(£Ту+1)(ртЕЫХ+>)- (6.9) р2Ту (Ti + твых) + р {Кгх + тх -f ту + твых) + 1 Формулу, определяющую ивых в интеграторе рис. 6-8, а, получим теперь как разность выходного сигнала ОУ и напряжения е , причем выходной сигнал ОУ (относительно земли) найдем, воспользовавшись равенством (6-7). После простейших преобразований получим вых (Р) = - вХ (Р)-ElX±l±l-. р\ (Т! + твь1х) + р (Ктг + тх + ту + твых) + 1 Найденное равенство говорит о том, что передаточная функция интегратора весьма мало зависит от постоянных времени ту и Твых- Действительно, (6-10) Г(р)=--EIl+J£±l-« p2Tv (Tt + твых) + р (Kti + тх + ту + Твь,х) + 1 рту 4- К К (РКЧ+ 1) (рту/к+1)РКh 4-1 Сравнивая (6-10) и (6-8), видим, что благодаря тому, что выходной сигнал снимается с интегрирующего конденсатора (рис. 6-8, а), а не с выхода ОУ относительно земли (рис. 6-5, а), из передаточной функции интегратора практически исчезают составляющие, зависящие от постоянных времени ту и тВЫх- ПОС в интегрирующих преобразователях позволяет исключить низкочастотную погрешность интегрирования. В частности, положительная обратная связь может быть введена в преобразователь по схеме рис. 6-5, а путем включения в него резистив-ного делителя, подающего часть выходного напряжения на 0 ... 42 43 44 45 46 47 48 ... 82 |












