Раздел: Документация
0 ... 7 8 9 10 11 12 13 ... 35 трансформаторная цепь с индуктивной реакцией, не имеющая этих отрицательных свойств. Если 5 > 1, то, пренебрегая емкостью при индуктивной реакции и индуктивностью при емкостной, из уравнения (3.5) можно получить 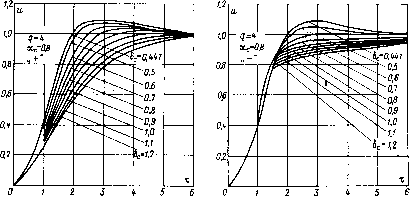 Рис. 3.22. Переходные процессы на фронте импульса при нагрузке ИТ магнетроном и индуктивной реакции в схеме генератора с частичным разрядом накопителя Рис. 3.23. Переходные процессы на фронте импульса при нагрузке ИТ магнетроном и емкостной реакции в схеме генератора с частичным разрядом накопителя О
Г 2 3 4 5 67 8 9 Ю1112 13 Рис. 3.24. Относительное удлинение фронта импульса при нелинейной нагрузке и сильной индуктивной и емкостной реакции приближенные формулы для расчета удлинения фронта импульса, учитывающие нелинейные свойства сопротивления нагрузки. 60 При индуктивной реакции ы °-9иа~1 гф=~/---гт<&.(3.27) Ф Rite 0,1 1 - аи - (1 - а)и" 1 При емкостной реакции гф = (1 - ос)ЩсС / --— .(328) 0,1 1 - аи - (1 - а)ич Кривые относительного удлинения фронта импульса, рассчитанные по формулам 7£ = tRtclL и тс = tal(R2cOnVK а = 0,5 и а = 0,8, приведены на рис. 3.24. Рассмотрение графиков подтверждает общую тенденцию уменьшения удлинения фронта с увеличением степени нелинейности нагрузки, особенно заметную при индуктивной реакции трансформаторной цепи. 3.4. ИСКАЖЕНИЯ ВЕРШИНЫ ИМПУЛЬСА При рассмотрении процесса формирования вершины импульса можно пренебречь влиянием индуктивности L и емкости С трансформаторной цепи (рис. 3.8), так как после окончания процесса формирования фронта импульса ток и напряжение нагрузки достигают значений, близких к установившимся, и далее, в течение времени действия импульса, изменяются незначительно, только вследствие медленного нарастания тока в относительно большой индуктивности L i. Такой характер протекания процессов в ИТ следует из самих требований, предъявляемых к ИТ и определяющих его конструкцию. С учетом сказанного процессы, протекающие при формировании вершины импульса, отображаются схемой, приведенной на рис. 3.25. Вследствие относительно малой длительности фронта приближенно можно считать, что процесс формирования вершины импульса начинается сразу же после возникновения импульса генератора. В действительности это не так, поскольку требуется некоторое время для заряда емкости трансформаторной цепи. Однако пренебрежение этим временем практически допустимо. В момент начала формирования вершины импульса ток в индуктивности намагничивания ИТ равен нулю. С течением времени этот ток возрастает, что приводит к увеличению тока генератора, увеличению падения напряжения на его внутреннем сопротивлении и в конечном итоге — к уменьшению напряжения на сопротивлении нагрузки. Для схемы на рис. 3.25 этот процесс описывается решением следующего, нормированного по времени и напряжению, нелинейного дифференциального уравнения первого порядка: [a+Cl-a)-1]- +м=0, (3.29) где и=и2 1ЩС я» и21(аЕг); т -*1 t (1 - a)Ric 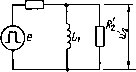 Рис. 3.25. Схема замещения трансформаторной цепи для анализа искажений вершины импульса После разделения переменных и интегрирования связь между временем и напряжением на сопротивлении нагрузки будет иметь следующий вид: а!пи t = (1 - a)Ric <7(1 -а) (1-й4 1) ч- 1 (330) Учитывая, что и = 1 - Дм, причем Дм < 1, относительное снижение напряжения на нагрузке к моменту окончания импульса с достаточной для практических расчетов точностью можно определить формулой (1 - a)R2ctK £,[а + (1 - a)q] 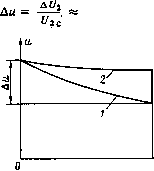 (3.31) Рис. 3.26. Искажения вершины импульса £ при пинейной (i) и нелинейной (2) на-t„грузке При линейном сопротивлении нагрузки, т.е. при «7 = 1, относительное снижение напряжения Дм= — 62 AU2 (1 - оОЛгги (3.32) Сравнение формул (3.31) и (3.32) показывает, что снижение напряжения на вершине импульса при нелинейной нагрузке меньше, чем при линейной, и тем меньше, чем выше степень нелинейности нагрузки. Таким образом, ив отношении искажений вершины импульса нелинейность нагрузки не препятствует, а способствует применению ИТ. Общий характер переходного процесса на вершине импульса виден на рис. 3.26. 3.5. ИСКАЖЕНИЯ СРЕЗА ИМПУЛЬСА После окончания импульса генератора в трансформаторной цепи возникает сложный переходный процесс, обусловленный тем, что к моменту окончания импульса во всех индуктивностях и емкостях трансформаторной цепи накопилась некоторая магнитная и электрическая энергия. Сложность переходного процесса связана с большим числом и распределенным характером параметров ИТ. Однако с еще большим основанием, чем при рассмотрении искажений фронта и вершины, задача исследования искажений среза импульса может быть упрощена до уровня математической модели трансформаторной цепи в виде дифференциального уравнения второго порядка. Это связано со следующими обстоятельствами. Переходный процесс в трансформаторной цепи после окончания импульса генератора определяется параметрами тех же структурных элементов схемы замещения, которые влияют на форму фронта и вершины. Поскольку искажения фронта и вершины являются главными факторами, определяющими возможность применения ИТ, все струк- < турные элементы схемы замещения выбираются так, чтобы эти искажения не превысили некоторых допустимых значений. Таким образом, параметры элементов схемы замещения определены требованиями к искажениям фронта и вершины и степень искажений среза оказывается производной величиной. Вследствие этого можно ставить задачу лишь установления фактических искажений среза и, в случае необходимости, уменьшения их такими методами, которые не увеличили бы искажений фронта и вершины. С другой стороны, искажениям среза обычно вообще придается второстепенное значение, так как они возникают после окончания рабочего цикла процессов в нагрузке и поэтому не могут оказать особого влияния на функционирование импульсного устройства. Если их влияние все же значительно, то его можно устранить или ослабить введением в трансформаторную цепь различного рода корректирующих двухполюсников. В связи с изложенным схему замещения трансформаторной цепи для исследования искажений среза импульса можно представить в упрощенном виде, приведенном на рис. 3.27. Переходный процесс в схеме иа рис. 3.27 после окончании импульса описывается решением следующего, также нормированного по времени и напряжению нелинейного дифференциального уравнения второго порядка: *«+ 2-1 * +«=0> drdi- me T=tS/LlC; «=«2/Ц[с(и); (3.33) (3.34) (3.35) (3.36) 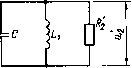 Рис. 3.27. Схема замещения трансформаторной цепи для анализа искажений среза импульса При q — 1, т. е. при линейной нагрузке, нелинейное уравнение (3.33) преобразуется в линейное: du d2u + 28,— +« =0- dr*dr Решение этого уравнения имеет следующий вид: и =е 6>т cositsinir при 6, < 1, 0, =\fl ch 0,т + ~ sh0,r j (3.37) (3.38) (3.39) приб! > 1, 0i = V6j - 1. Построенные по этим формулам зависимости приведены на рис. 3.28. Из формул и рисунка видно, что с увеличением коэффициента 61 длительность среза и амплитуда выброса напряжения на срезе уменьшаются. Приближенно длительность среза можно рассчитывать по формуле (3.40) гс TCVlic. Где тс - относительная длительность среза, полученная из графиков иа рис. 3.28 при соответствующем значении коэффициента S\ и взятая между оговоренными уровнями напряжения. При нелинейной нагрузке вследствие уменьшения со временем напряжения на нагрузке сопротивление нагрузки увеличивается, и тем сильнее, чем выше нелинейность нагрузки. Вследствие этого разряд емкости С через сопротивление нагрузки замедляется, длительность среза увеличивается. Весьма приближенно можно считать, что увеличение ее пропорционально q. Поэтому длительность среза при нелинейной нагрузке можно определять, увеличивая в q раз длительность среза для Линейной нагрузки, рассчитанную по формуле (3.40). Рис. 3.28. Переходные процессы на срезе трансформированного импульса при линейной нагрузке 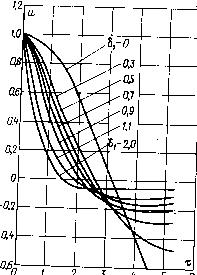 Отметим, что при отсутствии емкости С в трансформаторной цепи нелинейные свойства сопротивления нагрузки, наоборот, ускоряют переходный процесс на срезе и длительность среза уменьшается. 3.6, ЭНЕРГИЯ В РЕАКТИВНЫХ ЭЛЕМЕНТАХ ТРАНСФОРМАТОРНОЙ ЦЕПИ Ко времени окончания импульса генератора в индуктивностях и емкостях трансформаторной цепи накапливается некоторая энергия. После окончания импульса эта энергия рассеивается в собственно ИТ и активных элементах трансформаторной цепи. Та часть энергии, которая рассеивается в нагрузке, обычно нарушает нормальный режим работы нагрузки, несмотря на то что рассеяние происходит по завершении рабочего цикла. Процессы рассеяния ухудшают энергетические характеристики системы генератор - ИТ — нагрузка, а иногда нарушают нормальное функционирование устройства. Поэтому важно определить и обеспечить условия, при которых накапливаемая в трансформаторной цепи энергия минимальна. К моменту окончания импульса генератора в индуктивностях и емкостях схемы замещения (рис. 3.8) токи и напряжения можно считать установившимися. Тогда количество накопленной в этих элементах энергии выразится формулой LC=W22I2+CU22I2+I2L1iI2,(3.41) где ток намагничивания /о*02*н/*1-•(3-42) 0 ... 7 8 9 10 11 12 13 ... 35 |












