Раздел: Документация
0 ... 10 11 12 13 14 15 16 ... 35 изоляции обмоток: A2=U2/EA,(4.7) где £д — допустимая напряженность электрического поля в изоляционных промежутках обмоток (поперечная напряженность электрического поля). Приводя формулу (4.6) к толщине главной изоляции, получим L,=LS0FL,(4.8) где с учетом формул (1.13) и (2.3) V0w\pA2 nokpU2ги2 д2 ksyftr+gb2 Lso — -.- — -——5— -ё-v.4-") ftKki АВ Vs представляет собой индуктивность рассеяния простейшего идеализированного ИТ с однослойными цилиндрическими обмотками из бесконечно тонких проводов, рассчитанного на напряжение между обмотками, равное высшему вторичному напряжению. В формуле (4.8) множитель FL= — + Д12 d 1 + d2 --+ - д2 Зд2 представляет собой коэффициент, которым учитываются схемные и конструктивные особенности реальных обмоток. Введение в рассмотрение такого идеализированного ИТ придает формулам для расчета электромагнитных параметров ИТ единообразный универсальный характер и позволяет сопоставлять значения этих параметров при разных конструкциях и схемах обмоток. В мощных высоковольтных ИТ, где вторичное напряжение намного больше первичного и толщина изоляции между обмотками велика по сравнению с толщиной проводов обмоток, формула (4.9) имеет и самостоятельное значение, так как достаточно точна для практических расчетов. Обращает на себя внимание то, что индуктивность рассеяния обратно пропорциональна объему МС, т. е. уменьшение индуктивности рассеяния требует увеличения объема МС. Рассмотрим более сложную цилиндрическую вторичную обмотку, содержащую т слоев с числом витков w2lm в каждом слое (рис. 4.3 и 4.4). Такого типа обмотки применяются в повышающих ИТ, когда п> 1. Напряженность магнитного поля в проводе первичной обмотки и в изоляционном промежутке между обмотками будет такой же, как и в рассмотренном ранее случае. В проводах d2# различных слоев вторичной обмотки и изоляционных промежутках д2£ между слоями напряженность магнитного поля постепенно уменьшается. Так, в изоляционном промежутке А21 между первым и вторым слоем вторичной 78 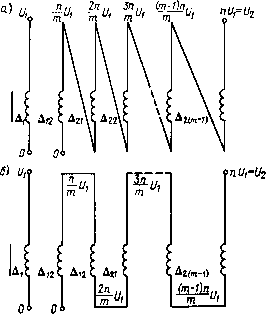 Рис. 4.3. Соединение слоев в многослойной обмотке при трансформаторном включении Рис. 4.4. Поперечное сечение трансформатора с цилиндрическими многослойными обмотками 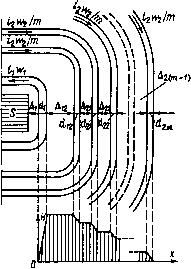 обмотки напряженность магнитного поля возникает от МДС не всех т слоев вторичной обмотки, а только т — 1 слоев, в промежутке между вторым и третьим слоем — только т — 2 слоев и т. д.; в последнем изоляционном промежутке Ат ] — от МДС только последнего слоя. Таким образом, в первом изоляционном промежутке вторичной обмотки (д21) i2w2 Ям- («-!); во втором промежутке (д22) Я„=-(я-2); в произвольно выбранном промежутке (А2к) i 2 w 2 Hik = —— (m-k). hm Суммирование магнитной энергии, сосредоточенной во всех изоляционных промежутках вторичной обмотки, приводит к следующему выражению: от - lMni?w?p от - 1 2 Wlk= JLLifl 2 А2к(т-к)2. к = 12т h к = I Аналогично в проводах вторичной обмотки hw2 Iх п21х = —— т - -— 1Х йот \ d21 иiW2 ( , х \ Я»**-*1Г (™-*- d~) н = l2W2 х 2тХ Лот d2m Суммирование энергии, сосредоточенной в проводах вторичной обмотки, приводит к выражению 2 Wd2hI 2 Г (m-k-~) dx = к = 02й от t = o 0 \/ 2 d2kf(k,m), 32А к = 0 •»)-3(1-s)(1-*-si)+i- Суммируя энергию, сосредоточенную во всех элементах обмотки трансформатора, и сопоставляя ее выражение с формулой для магнитной энергии (4.4), получим следующее выражение для индуктивности рассеяния обмоток трансформатора (рис. 4.3) : UnWnD Г1 ОТ — 1 (2) =- д12 + —1 2 А2к(т-к)2 + + г-1 + \ 2 d2kf(k,m) 33 Л = 0 или, после приведения к числу витков первичной обмотки, — Ls = LS0FL ,(4.10) где 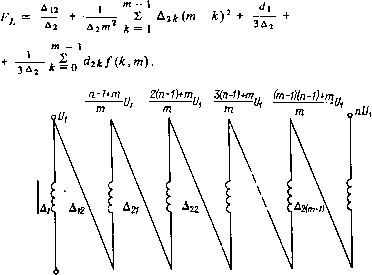 0 Рис. 4.5. Соединение слоев в многослойной обмотке при автотрансформаторном включении Подобным методом может быть вычислена индуктивность рассеяния при Произвольном взаимном расположении элементов цилиндрических обмоток. Можно также показать, что при автотрансформаторном включении обмоток (рис. 4.5) индуктивность рассеяния уменьшается 81 в(и — 1)2/и2 раз по сравнению с рассмотренными случаями трансформаторного включения. Следует отметить, что полученные формулы справедливы, когда суммарный габарит намотки Д = Aj + dx + А13 + 2(Д2£ + d2k) Л и все слои первичной и вторичной обмотки расположены строго один над другим. При взаимном смещении слоев по оси намотки или при уменьшении длины слоев по мере приближения к наружному слою (с увеличением номера слоя) индуктивность рассеяния увеличивается. Отметим также некоторые факторы, влияющие на индуктивность рассеяния и трудно учитываемые при аналитическом расчете. Как показывает опыт, индуктивность рассеяния, почти ие зависит от магнитной проницаемости МС. Однако само наличие МС с д 1 несколько (незначительно) увеличивает индуктивность рассеяния. С уменьшением отношения диаметра провода к шагу намотки при неизменной длине катушки также увеличивается индуктивность рассеяния, что трудно поддается аналитическому учету. Некоторое представление о влиянии коэффициента заполнения обмотки проводом на индуктивность рассеяния дает нормализованная кривая Л/,(Л2), построенная на основе экспериментально определенных, значений индуктивности рассеяния в цилиндрической однослойной обмотке без МС (рис. 4.6). В процессе измерений индуктивности рассеяния коэффициент 2,5 щ 1,5 0,5\
Рис. 4.6. Влияние шага намотки на электромаг- 0 0,2 Ofi 0,6 08 1,0 нитные параметры цилиндрических обмоток заполнения первичной обмотки проводом &dj —dy\h Hi » 0,9 (А н - шаг намотки) был постоянным. Длина, средний периметр, число витков обмоток и толщина изоляционного промежутка Д12 между обмотками также были постоянными. Коэффициент заполнения вторичной обмотки kj2 = d2jhH2 уменьшался путем сокращения числа параллельно включенных проводов во вторичной обмотке. Нормализация произведена по отношению к значению индуктивности рассеяния при Лу2 = 0,9. Ход кривой kL указывает на резкий рост индуктивности рассеяния при*<22 < 0,5. Влияние различных трудноучитываемых факторов придает особое значение экспериментальному определению индуктивности рассеяния ИТ. 4.3. ДИНАМИЧЕСКИЕ ЕМКОСТИ Замена распределенных емкостей обмоток ИТ сосредоточенными основана на том же энергетическом принципе, что и расчет индуктив-ностей рассеяния. Если известны геометрия обмоток и распределение напряжения на них, то можно вычислить энергию электрического поля, сосредоточенного между соответствующими элементами конструкции ИТ. Приравнивая энергию, рассчитанную таким образом, энергии выраженной через сосредоточенную емкость и напряжение на первичной обмотке, можно определить сосредоточенную емкость как энергетически эквивалентную распределенной, приведенную к напряжению первичной обмотки. Определенная таким образом емкость носит название динамической емкости. Вычислим динамические емкости ИТ с многослойными цилиндрическими обмотками, слои которых соединены по схемам на рис. 4.3 и 4.5, полагая, как это обычно и бывает на практике, что МС и начало первичной и вторичной обмоток имеют нулевой потенциал. Если бы между первичной обмоткой и МС действовало постоянное напряжение, то при А > Дь что обычно выполняется в ИТ, электрическое поле в изоляционном промежутке At было бы практически однородным. По этой причине первичная обмотка и МС могли бы рассматриваться как эквипотенциальные поверхности конденсатора с параллельными пластинами. Емкость такого конденсатора выражается известной формулой С= e0eSIA t = e0eph fAv, где e — относительная диэлектрическая проницаемость материала изоляции. Однако, вследствие того что на первичной обмотке ИТ импульсное напряжение, она не может рассматриваться как эквипотенциальная поверхность. Поэтому при расчете емкости необходимо учитывать распределение напряжения в обмотке, имеющее сложный пространственно-временной характер, который обусловлен распределенным характером индуктивности, емкости, сопротивления обмотки, и взаимной индуктивности витков [8]. Картина распределения напряжения непрерывно меняется во времени — до тех пор, пока не закончится 0 ... 10 11 12 13 14 15 16 ... 35 |












