Раздел: Документация
0 ... 12 13 14 15 16 17 18 ... 35 С учетом поверхностного эффекта сопротивление переменному току провода круглого сечения при протекании через него синусоидального тока частотой / выражается с помощью функций Бесселя аргумента где d — диаметр провода [3]. При протекании прямоугольных импульсов тока аргумент функций Бесселя можно связать с длительностью импульса приближенной формулой, которая для температуры 75 °С имеет вид [3] Z = 6d/y/T. Это позволяет на основании точного решения задачи о влиянии поверхностного эффекта собственно проводов при синусоидальном токе на сопротивление переменному току найти соответствующее приближенное решение для импульсного режима. С приемлемой для практических целей точностью увеличение сопротивления уединенного прямого провода круглого сечения при поверхностном эффекте можно определить по заимствованному из работы [3] графику (рис. 4.9). Что каса-
Рис. 4.9. Относительное увеличение сопротивления проводов при поверхностном эффекте ется проводов прямоугольного сечения, удовлетворительного решения соответствующей задачи для импульсного режима работы пока не найдено. Приближенно увеличение сопротивления такого провода при Ъ> 2а можно определить по графику на рис. 4.9, полученному посредством интерполяции данных [3, 19, 20]. Определить увеличение сопротивления проводов обмоток вследствие поверхностного эффекта самой обмотки в импульсном режиме — еще более сложная задача, которая, насколько известно, не решена. Поэтому единственно целесообразным и относительно достоверным представляется решение этой задачи-яо методике расчета дополнительных потерь в обмотках силовых трансформаторов [20], апробированной многолетним и масштабным производством силовых трансформаторов. 90 Применительно к ИТ на основании работы [20] и с учетом работы [3] для усредненного увеличения (вследствие поверхностного эффекта обмотки) сопротивления проводов круглого и прямоугольного сечения можно получить следующие формулы: г(к d2\ 2 кп.о==1 + 11,5-Ю"14 (л2-0,2);(4.25) 0\ ГиР / *п.о ==1+24,9-Ю-14) (п2 -0,2),(4.26) го\иР ) где к0 — коэффициент заполнения обмотки проводом; п -» число слоев провода в обмотке; для однослойных обмоток второй член в формулах должен быть умножен на 0,8. Из формул видно, что в однослойных обмотках поверхностный эффект обмотки минимален и, следовательно, для его уменьшения целесообразно применять именно простейшие однослойные обмотки. В конечном итоге сопротивление переменному току можно рассчитывать по формуле r Р s "•п.пп.о, м где коэффициенты поверхностного эффекта провода и обмотки кп,п и кп.о определены описанным способом. В связи с изложенным уместно отметить, что при расчете сопротивления переменному току принят ряд допущений, степень обоснованности которых практически не исследована. Так например, введение в рассмотрение синусоидального процесса, эквивалентного импульсному [3], нуждается в более строгом обосновании. 4.5. ЦИЛИНДРИЧЕСКИЕ ОБМОТКИ Наибольшее распространение в ИТ получили цилиндрические обмотки, так как они обладают малой индуктивностью рассеяния, конструктивно просты и технологичны. В зависимости от назначения ИТ и предъявляемых к его параметрам требований цилиндрические обмотки могут иметь различное число и взаимное расположение слоев и секций, а также различные схемы их соединения. Применяется как трансформаторное, так и автотрансформаторное включение обмоток, причем последнее — ввиду, того что при небольших коэффициентах трансформации (л < 5) можно уменьшить индуктивность рассеяния ИТ. Обмотки могут быть однослойными и многослойными и располагаться как на одном, так и на обоих стержнях МС. Предпочтение обычно отдается однослойным обмоткам, так как они проще в изготовлении 91 и надежнее при эксплуатации. Для уменьшения индуктивности рассеяния и более полного использования длины МС обмотки обычно располагают на обоих стержнях. При составлении схемы соединения и размещении секций и слоев обмоток исходят из требований минимальной разности потенциала 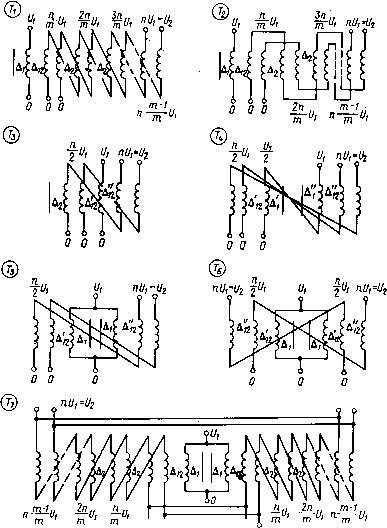 6 66 0 0О Рис. 4.10. Типовые схемы обмоток ИТ между обмотками, между обмотками и МС, а также минимальных габаритов ИТ с учетом требований к электрической прочности, индуктивности рассеяния и динамическим емкостям. 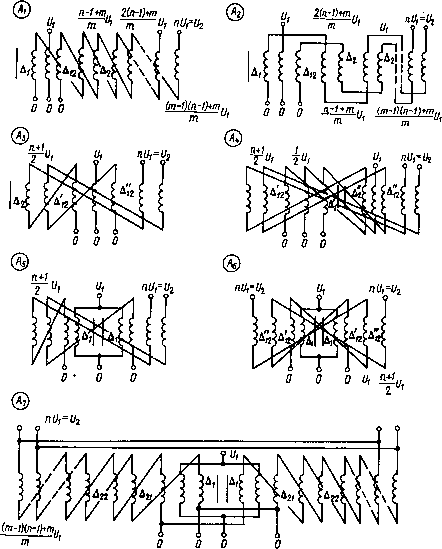 Рис. 4.11. Типовые схемы обмоток импульсных автотрансформаторов Практикой проектирования ИТ различных параметров и назначения выделен ряд типовых схем в соединения секций и слоев, где эти общие принципы удовлетворяются более или менее полно. Такие схемы трансформаторов (индекс Т) и автотрансформаторов (индекс А) приведены на рис. 4.10 и 4.11, а в табл. 4.1 Таблица 4.1. Выражения для электромагнитных параметров-трансформаторов (рис. 4.10) Индекс Fen 1*2 (п Яг т) т2 А12 Ъп*(т - 1) ~2 . д т - 1 Д,2 + Б (т-к)2 + т к = \ dy + 2md2 JL + ("Лп2(т - 1) Д,„2* 2л тя*Д 12 т А2 А12 + Д,2 + di + 4d2 (л ,Т2Г + 6я2 Тбл -i- (л Т2)2 4Д, 4Д< 4А 1 7 1/17 —— + -+ — + 4Д 4д, 4 Д*2 ДГ2< 1 / , „ di+2d2\ д12+ди+ — \ X (л Т1)3 + (и Т2)2 + б"2 ?6л + (л Т2)-Д14Д124Дц 1 / ,d1+2d2\ — + - +л -5-— д12Д«2ДД Д12"2 2~ + 3 2m *: = ! d, + 2m</2 Б (т - к) 2 + 2 2(л Тст)2 6л2 (m - 1) Д1 + т2А\2т2 Д2 и 4.2 — соответствующие формулы для расчета индуктивности рассеяния и суммарной динамической емкости обмоток. Значения электромагнитных параметров приведены к числу витков первичной обмотки и толщине главной изоляции. В тех случаях, когда ИТ предназначен для согласования генератора импульсного напряжения с высокочастотным генератором (магнетрон, усилительный клистрон и др.), Таблица 4.2. Выражения для электромагнитных параметров автотрансформаторов (рис. 4.11)
0 ... 12 13 14 15 16 17 18 ... 35 |












