Раздел: Документация
0 ... 9 10 11 12 13 14 15 ... 35 При работе ИТ на нелинейные виды нагрузок обычно значительно удлиняется срез импульса, нто в ряде случаев недопустимо. Весьма эффективен и прост способ укорочения (уменьшения длительности) среза, основанный на использовании нелинейных свойств характеристики намагничивания МС при насыщении. Как 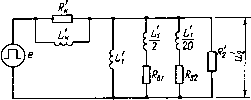 Рис! 3.33. Схема замещения ИТ с коррекцией вершины импульса видно из формулы (3.40), длительность среза можно сократить, уменьшив в момент окончания импульса генератора индуктивность намагничивания ИТ. Путем такой регулировки размагничивающего тока, чтобы в этот момент наступало насыщение стали МС. В МС из электротехнических сталей индуктивность можно уменьшить в 10s раз, в МС из пермаллоев - в 105 раз, вследствие чего удается сократить длительность среза иа один-два порядка. Однако вследствие уменьшения индуктивности намагничивания снижается коэффициент затухания трансформаторной цепи Sj при формировании среза импульса, что видно из формулы (3.36). Поэтому, как показывает решение уравнения (3.38), при коэффициентах затухания, меньших единицы, возникает выброс напряжения на срезе импульса -тем больший, чем меньше коэффициент затухания. Необходимо отметить, что в большинстве случаев нагрузка обладает вентильными свойствами. Поэтому после уменьшения напряжения на срезе импульса до нуля рассеяние энергии, накопленной в электромагнитных элементах трансформаторной цепи прекращается и нагрузка перестает оказывать шунтирующее влияние. Вследствие этого коэффициент затухания дополнительно резко уменьшается, что еще более увеличивает выброс напряжения отрицательной полярности на срезе импульса. Для устранения выброса напряжения на срезе параллельно нагрузке устанавливается специальный, так называемый подавляющий диод. Полярность включения диода выбирается соответствующей полярности напряжения выброса на срезе импульса. Это обеспечивает рассеяние энергии в цепи диода в течение выброса напряжения, благодаря чему коэффициент затухания увеличивается и амплитуда выброса уменьшается. Схемы включения и расчет цепи диода рассмотрены в специальной литературе по проектированию импульсных генераторов [17, 18]. Главные соображения по выбору диода и расчету цепи состоят в следующем: диод должен выдерживать с некоторым запасом, определяемым особенностями эксплуатации, полное напряжение импульса генератора; цепь диода должна рассеивать мощность, определяемую формулой Рц — WjgF, где— энергия, накоплен- ная в трансформаторной цепи ко времени окончания импульса [см. формулу (3.43)]. ГЛАВА ЧЕТВЕРТАЯ ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ ОБМОТОК 4.1. СВЯЗЬ МЕЖДУ ЭЛЕКТРОМАГНИТНЫМИ И КОНСТРУКТИВНЫМИ ПАРАМЕТРАМИ. ИНДУКТИВНОСТЬ НАМАГНИЧИВАНИЯ Из рассмотрения причин искажений трансформированного импульса следует, что все виды искажений определяются как заданными электромагнитными параметрами внешних частей трансформаторной цепи, так и электромагнитными параметрами схемы замещения собственно ИТ. Значения параметров схемы замещения ИТ (индуктивность намагничивания, индуктивность рассеяния и суммарная динамическая емкость обмоток) определяются электромагнитным расчетом, и очередной этап проектирования ИТ состоит в переходе от схемы замещения к конструкции. Главные размеры МС и обмоток должны быть выбраны так, чтобы обеспечить требуемые значения электромагнитных параметров схемы замещения ИТ и, по возможности, минимальное сопротивление обмоток. Для решения этой задачи необходимо установить функциональные связи между электромагнитными параметрами схемы замещения и размерами конструкции ИТ. В настоящей главе рассматриваются принципы установления таких функциональных связей и приводятся формулы для расчета электромагнитных параметров схемы замещения по конструктивным параметрам для различных конструкций и схем обмоток ИТ, лежащие в основе конструктивного расчета ИТ. Индуктивность определяется как отношение потокосцепления катушки к протекающему через катушку току, r.e.L = Ф/г = м>Ф0/7. В катушке с МС из стали, магнитная проницаемость которой велика по сравнению с магнитной проницаемостью воздуха, лишь незначительная часть магнитных силовых линий в виде потока рассеяния замыкается вне МС. Поэтому при определении индуктивности намагничивания ИТ можно считать, что весь магнитный поток сосредоточен в МС, поперечное сечение которой вдоль всей ее длины постоянно. Оба этих предположения справедливы для практических конструкций ИТ. Для определения индуктивности намагничивания рассмотрим трансформатор, первичная обмотка которого содержит wt витков (рис. 4.1). Напряженность магнитного поля, которое создается намагничивающим током трансформатора вдоль элементарного слоя dx, лежащего в плоскости сечения набора пластин МС, согласно закону полного тока ■[*•*(£-J я* Магнитный поток в элементарном слое с учетом коэффициента заполнения сечения d<bx = ц0цНхЬка(1х 1 Из этого выражения индуктивность намагничивания определится формулой Lt = w, Ф 1»0 «1 Wl "г m0mw2e6*a 12 у- / d<bx =- In - (4.1) 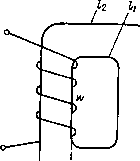
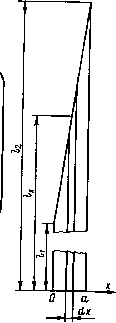 Рис. 4.1. Схема для определения индуктивности намагничивания При /2//i < 2, что обычно для практики, to — •121 /Гл; * /Ти£ = г •<4-2) Поэтому для вычисления индуктивности намагничивания обычно пользуются упрощенной формулой, учитывающей соотношение (4.2): L>= w}Sk\.(4.3) Упрощенная формула при /2//- =2 дает результат всего лишь на 4% меньший, чем точная формула (4.1). С уменьшением отношения 12/1у точность возрастает. Формулы (4.1) и (4.3) получены в предположении, что магнитная проницаемость стали МС не зависит от магнитной индукции, что является определенным упрощением. В действительности, если ИТ работает в области индукций, где магнитная проницаемость увеличивается с повышением индукции, концентрация магнитного потока в области коротких силовых линий (во внутренней области МС) возрастает и фактическая индуктивность намагничивания оказывается больше вычисленной по формуле (4.3). При работе ИТ в области индукций, где магнитная проницаемость уменьшается с повышением индукции, действительная индуктивность оказывается меньше вычисленной. Однако расхождение, если нет насыщения стали МС, обычно невелико и не учитывается на практике. Значительно более важно то, что при больших, близких к индукции насыщения, приращениях индукции насыщение стали во внутренней области МС наступает раньше, чем во внешней, где вследствие большей длины силовых линий напряженность магнитного поля меньше. По этой причине в мощных ИТ, режим работы которых характеризуется большими приращениями индукции, отношение l2lh приходится уменьшать примерно до 1,5, а в отдельных случаях и до меньших значений. 4.2. ИНДУКТИВНОСТЬ РАССЕЯНИЯ Индуктивность рассеяния как сосредоточенный параметр удобно определять исходя из того обстоятельства, что магнитное поле рассеяния создается частью тока нагрузки. В этом магнитном поле сосредоточена магнитная энергия, которая может быть вычислена, если известны геометрические соотношения между отдельными элементами конструкции ИТ и ток нагрузки. С другой стророны, магнитная энергия выражается известным соотношением W=ii2/2.(4.4) Таким образом, определив энергию поля рассеяния и зная ток-нагрузки, из в.ыражения (4.4) можно найти индуктивность, эквивалентную индуктивности рассеяния ИТ [2, 3,7]. Расчет магнитного поля рассеяния облегчается тем, что для уменьшения индуктивности рассеяния в ИТ применяются обмотки относительно большой длины с минимальным, определяемым требованиями 75 достаточной электрической прочности изоляционными расстоянием между обмотками. Такие обмотки подобны длинным соленоидам, магнитное поле внутри которых отличается высокой степенью однородности. Это позволяет пренебречь краевым эффектом обмоток и считать магнитное поле однородным, что значительно упрощает расчеты как самого поля, так и сосредоточенной в нем энергии. Так как МДС первичной и вторичной обмотки вследствие малого рассеяния приблизительно равны и токи в обмотках обтекают МС в противоположных направлениях, то напряженность магнитного поля между обмотками примерно равна напряженности поля в соленоиде с таким же числом витков, а магнитная энергия поля рассеяния может считаться сосредоточенной 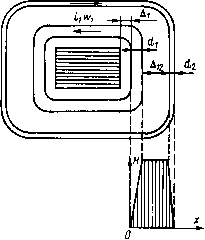 Рис. 4.2. Поперечное сечение трансформатора с цилиндрическими однослойными обмотками в пространстве между обмотками. Что касается распределения тока в обмотках, то его плотность, вообще говоря, неодинакова по сечению провода каждой обмотки. При расчете могут быть приняты следующие допущения: 1) ток концентрируется на наружной поверхности провода первичной обмотки и на внутренней поверхности провода вторичной обмотки; 2) ток концентрируется в центральной части сечения проводов обмоток. Реальное распределение тока — обычно среднее между указанными предельными. Так как диаметр или толщина проводов обмоток в ИТ, как правило, значительно меньше размера изоляционных промежутков, то предпосылка о наиболее вероятном — равномерном распределении тока в проводе не вносит чрезмерно большой погрешности. 76 С учетом изложенного вычислим индуктивность рассеяния ИТ с простейшими цилиндрическими однослойными обмотками (рис. 4.2). В соответствии с принятой предпосылкой о распределении токов напряженность магнитного поля в проводе первичной обмотки с размером di равномерно нарастает в направлении х, остается постоянной в изоляционном промежутке размером д12 между обмотками и в проводе вторичной обмотки равномерно уменьшается до нуля. Если высота катушки Л, то напряженность магнитного поля в различных элементах обмотки будет выражаться следующими формулами: в проводе первичной обмотки „ *\*>1 X Н™1 х Hvc - -j— - -h ; в пространстве между обмотками в проводе вторичной обмотки Плотность энергии магнитного поля в воздухе и меди обмоток W =НВ12 = ц0Я212. Энергия, сосредоточенная во всем объеме поля рассеяния, мойр W = did, + д12 + d2 J Hlcdx +H?2Al2 + J H2\dx .0di + A12 ••2...2. m02W2P /d, +d2 \ 1ди +.(4.5) Из сопоставления формул (4.4) и (4.5) индуктивность рассеяния, приведенная к числу витков вторичной обмотки, мон>2р /di +d2 Ls{2) = -д— Ai2 + учитывая, что w2 = nwi, после приведения к виткам первичной обмотки получим тт MoWiP Л di +d2\ f(l) =i= —— Uia+ -— •(4-6) В практических расчетах, особенно при выявлении общих для ИТ закономерностей, удобно оперировать условной толщиной главной 77 0 ... 9 10 11 12 13 14 15 ... 35 |
||||||||||||||||||||||












