Раздел: Документация
0 ... 37 38 39 40 41 42 43 ... 177 R := subnmtnx(N,01rows(M) - l,cols(M),2cols(M) - I) Проверка разложения: (8.307 9.872 9.149 0 -0.742 -3.613 Ч).487 J
Сингулярное разложение Сингулярным разложешчем матрицы Ы размера пхт (л 2 т) называется разложение вида M~V-s-VT, где Vv\ V — диагональные матрицы размерности соответственно пхл и mxm,s — диагональная матрица с сингулярными числами матрицы М на диагонали. Для решения задачи сингулярного разложения в Mathcad существуют следующие встроенные функции. □svds{M). Определяет вектор, содержащий сингулярные числа матрицы М. □svd(M). Функция сингулярного разложения. Результат выдает в виде единой матрицы. Сингулярное разложение полезно в связи с тем, что оно зачастую дает возможность решать практически вырожденные системы линейных уравнений, с которыми не справляются стандартные методы. 3.3.9. Функции max и min Одной из самых распространенных матричных задач является задача выбора наибольшего элемента в массиве. С подобной проблемой мы уже сталкивались, когда при определении нормы матрицы требовалось выбрать наибольшую сумму элементов строк или столбцов. Также к задаче такого рода сводится поиск экстремума функции (локального или глобального) матричным методам. Естественно, Mathcad не был бы самой совершенной математической программой, если бы не позволял делать этого предельно быстро и просто. Для выбора наибольшего или наименьшей* элемента существуют две специальные функции; □ птах(М) — выдает значение наибольитего элемента матрицы, Q min(M) — функция выбора наименьшего элемента Если элементы представлены комплексными числами, то при использовании функций min и max результат выдается исходя из величины их действительной части. Пример 3.48, Использование функций min и max max(M) = 8 min(M) = 1
Глава 4. Программирование Большинство людей, никогда не сталкивавшихся в своей практике с решением задач с помощью программирования, считают эту область человеческого знания сложной, малопонятной и доступной лишь специалистам. Это так и не так в одно и то же время. Конечно, посидеть вечерок над учебником для того, чтобы быть способным написать программу управления сложной автоматической системой — это, конечно, нереально. Но за относительно небольшой отрезок времени освоить тот минимум, который необходим для успешного решения большинства математических задач — это, в принципе, возможно, причем в случае любого современного языка программирования высокого уровня. Позиция компании Mathsoft относительно того, как должна быть построена математическая система, была и остается следующей: Mathcad должен быть настолько прост, чтобы быть доступным пониманию всех, кому приходится сталкиваться с расчетами, будь то ученый, инженер или простой студент. Поэтому в первых версиях системы Mathcad языка программирования не было вовсе: авторы посчитали, что введение такого сложного (в массовом понимании) элемента, как язык программирования, не впишется в общую концепцию пакета. Однако на практике без элементов программирования обойтись довольно сложно (это потребовало бы введения огромного количества встроенных функций, предусматривающих все возможные и невозможные запросы пользователя). Поэтому создатели Mathcad, желая сохранить простоту своего детипш, пошли на довольно нестандартный шаг — они создали систему программирования без программирования. Звучит довольно странно, не правда ли? Попробуем объяснить, что означает этот термин. Все дело в том, что любая программа строится на своего рода трех китах алгоритмизации: следовании, цикле и условии. Последовательное выполнение команд (следование) обеспечивалось логической активностью рабочих листов Mathcad. Вместо оператора цикла for в Mathcad было предложено использовать ранжированные переменные, цикл while имитировался посредством функции until (последняя со времен Mathcad 2000 считалась устаревшей, но пользователи продолжали ее активно применять, поэтому В Mathcad 12 разработчики «воскресили» ее), для введения условия существовала встроенная функция if. Куда больших изощрений требовало задание рекуррентных соотношений, но и это было возможно. Построенные по описанным принципам алгоритмы получались резка отличными по своей форме от выработанных норм и традиций, поэтому программами их можно было назвать с очень зна- чительными оговорками. При этом желаемого упрощения достигнуто не было, скорее наоборот — алгоритмы и Mathcad получались запуганными и причудливо-сложными. Поэтому можно вполне смело утверждать, что эксперимент Mathsoft, связанный с попыткой создать качестве иную математическую систему, которая бы могла эффективно работать вообще без использования программировании, оказался неудачным. В следующем примере вы можете сравнить два способа программного решения задачи в Mathcad. Внимательно изучив его, вы наверняка поймете преимущества использования языка програмшфования. Пример 4.1. Решение квадратного уравнения альтернативными программными методами Я*);=х -5*+ 4 А т= fjx) coeffs, J -* А •= reverse (А) Solution :«И DiO, SolauooProg<»,b,c) : 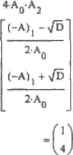 "No real roots" D<- Ь - if D20 4-*-c -b -Vd 2а return х "No real roots" SolutionProg( I, i, I) Solution Pro S> I 1 г "No reaJ rood" Solution Осознав, что отсутствие возможности программирования сильно ослабляет позиции пакета Mathcad, компания Mathsoft дополнила его профессиональную версию соответствующим элементом И, следует признать, сделала это очень качественно. Язык программирования Mathcad содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам гтр ft грамм иря ватты ц Кроме того, у него есть одно очень крупное преимущество: язык программирования Mathcad предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов). Конечно, можно за несколько вечеров освоить все, что нужно для решения математических задач, например в Delphi, ио для этого потребуется, чтобы у вас были хотя бы начальные знания об основных ходах и приемах в программирован ни. Для системы программирования Mathcad вам не понадобится ровным счетом никаких познания в этой области — будет достаточно одной лишь интуиции. Возможности же. которые пы получите, освоив эту систему, ограничены лишь конечной производительностью компьютера! В данной главе мы рассмотрим операторы и важнейшие приемы программирования в Mathcad. Практику ггрограмиирова пня мы отработаем при решении задач в остальных 0 ... 37 38 39 40 41 42 43 ... 177 |












