Раздел: Документация
0 ... 34 35 36 37 38 39 40 ... 177 Пример 3.37. Сортировка строк матрицы Транспонируем исходную матрицу U 5 П М : I 0 3М:=МТ v.2 -41 1; Задаем с помощью ранжированной переменой никл. Задействовав функцию sort(V), поочередно сортируем все столбцы транспонированной матрицы laS<M<°>) М1 := sort К) Транспонируем полученную матрицу (мри этим отгортнравашые столбцы становятся строками) и получаем необходимый результат. Ml :=МГ Ml = \ А 5 О 1 3 41 -41 2 2) Если же попытаться отсортнропать матрицу, задав цикл непосредственно для функции rsort(M.i), то в результате получится вложенный массив, содержащий в качестве элементов матрицы, у которых отсортировано только цо одной строке. Конечно, проблему эту обойти можно — но решение при этом очень усложнится. Так что в таких случаях лучше создавать алгоритмы, подобные вышеописанному. □ reverse(V), Эта функция переставляет элементы вектора в обратном порядке. Используется, как правило, в том случае, если элементы отсортированного вектора или матрицы должны располагаться по принципу «чем ниже — тем меньше». Использование же reverse(V) в данном случае необходимо, поскольку функции сортировки расставляют их в противоположном порядке. В основе работы функций sort(V). csort(M,i) и rsort(M,i) лежит алгоритм так называемой пирамидальной сортировки. Суть его заключается в представлении массива в виде бинарного сортирующего дерева — пирамиды (рис. 3.6). 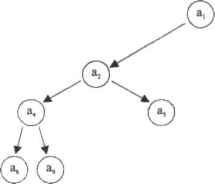 1\ 1\ (S) (5) 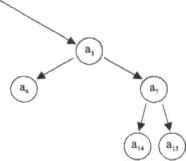 Любое бинарное дерево содержит только один корневой узел, не имеющий предшественников. Другие же узлы имеют одного предшественника и одного или двух преемников. Бинарное дерево будет являться пирамидой в том случае, если выполняется следующее условие: а;>ая и а£а~ г Другими словами, каждый элемент пирамиды должен быть меньше своего предшественника, либо равняться ему. Тогда максимальный элемент массива будет помещен в корневой узел. Любой же фрагмент «хвостовой » части пирамиды также является пирамидой. Алгоритм пирамидальной сортировки требует порядка N-log3N операций (meN — размер массива) и включает в себя 1>еализацию двух этапов: построение бинарной пирамиды и непосредственно сортировка ее элементов. Обсудим детально каждый их них. Начнем построение пирамиды с элементов а~¥..аК1 поскольку часть массива при i>N/2 удовлетворяет свойству иирамиды.таккакего элементы не имеют преемников. Будем наращивать пирамиду, добавляя па каждом шаге по одному элементу, стоящему перед уже готовой частью. Допустим, что построение пирамиды началось с элемента ав (см. рис, 3.6). В этом случае нам необходимо рассмотреть предшественника — элемент а( — и двух его преемников — элементы а5 и а, нз которых выбираем наибольший. Если этот преемник (предположим, ag) оказывается больше своего предшественника &4, то их меняют местами (<просеивают>а4 к основанию пирамиды). Таким образом, элемент аа попадает на предыдущий уровень. Аналогичные операции проводятся с оставшимися элементами массива а-а. Далее переходим к следующему шагу — повторяем все вышеописанные действия с элементами на уровне, находящемся перед рассмотренным, а «опустившиеся» элементы «просеиваем» по веточке бинарного дерева к основанию до тех пор, пока весь массив не превратится в пирамиду (то есть пока не будет соблюдаться условие а(>а2. и а(ааин). После того как пирамида построена, переходим к следующему этапу — непосредственной сортировке ее элементов. Как вы помните, первый элемент, находящийся в корневом узле, — максимальный. Меняем его местами с последним элементом пирамиды а...а>1и больше не возвращаемся к нему. Затем «просеиваем» новый верхний элемент и получаем пирамиду а.а, с которой повторяем ту же операцию до тех пор, пока размер массива не уменьшится до одного элемента. Таким образом, на каждом шаге в конце массива оказывается максимальный элемент текущей пирамиды. В результате формируется упорядоченная последовательность элементов по возрастанию. 3.3.4. Функции слияния и разбиения матриц Выделение части матрицы Для выбора из матрицы элемента с известными индексами в Mathcad существует специальная функция hlookup(i,Mj), где i — номер строки, j — номер столбца, М — некоторая матрица. При решении многих задач возникает необходимость выделить в отдельные пары соответствующие элементы двух матриц. Наиболее быстро и просто сделать это можно с помощью специальной функции lookop(r,M,N), где г — известный скаляр, М и N — соразмерные матрицы. Функция эта выводит значение того элемента матрицы N, который занимает 8 ней такое же положение, как скаляр г в матрице М. При этом, если несколько элементов матрицы М равны г, то в качестве ответа выдается векторе соответствующими всем им значениями элементов матрицы N. Пример 3.38. Выделение элементов из матриц ?\ 2 3>(\ 2 Ъ\ М : 3 2 5 N ?" lookup{2,M,N) С) 4 5 6 Ч7 8 9; Ьюокир(3,М,1)*(5) Очень часто на практике возникает задача, обратная рассмотренной; по известному элементу определить его положение в матрице. Так как иногда приходится работать с очень большими матрицами, визуальный поиск нельзя считать универсальным. Поэтому для выполнения такой задачи в Mathcad существует специальная функция match(z,H), где г — скаляр, положение которого определяется, М - матрица, в которой ведется поиск. Пример 3.39. Определение положения элемента матрицы match(3,M) и Для выделения из матрицы произвольной подматрицы в Mathcad существует специальная функция 5ubmatrix(M1rl,r2,cl,c2), где М — некоторая матрица, п и г? — верхняя и нижняя граничные строки, cl н с2 — соответственно граничные столбцы извлекаемой подматрицы, С помощью этой функции, правильно определив границы, можно выделить отдельные строки или столбцы матрицы. Пример 3.40. Использование функции submatrix 2 3 4 М :-1 6 7 8 Ml :=submatru<M.O,t,0,l)Ml а Выделение отдельно™ столбца илн строки: Col: = submatrix(M ,0,2.1,1) Col = 7 V Row : = siibmat ri х(М ,0,0,0,2) Row = (2 3 4) Функции слияния матриц Иногда при решении задач возникают проблемы, требующие слияния нескольких векторов или матриц. Иа практике функции слияния матриц используются очень часто, поэтому их нужно постараться запомнить. 0 ... 34 35 36 37 38 39 40 ... 177 |












