Раздел: Документация
0 ... 31 32 33 34 35 36 37 ... 177 галочкой функции csgn. Связано это с тем, что Mathcad по умолчанию рассматривает все числа как комплексные Оператор assume позволяет ввести ограничения на мара-метр R, поскольку радиус может быть только действительным числом (что задается с помощью служебного слова real). Так, путем несложных преобразований мы пришли к корректному ответу. В Mathcad определитель находится с помощью LU-раэложения Как это делается, демонстрируется в гл. 8 (в разделе, посвященном решению систем линейных уравнений) 3.2.6. Модуль вектора Модулем (или абсолютной величиной) вектора называется длина изображающего его отрезка. Модуль вектора (Vector Magnitude) по определению равен квадратному корню на суммы квадратов его элементов. Геометрический смысл модуля вектора - это длина отрезка, соединяющего точку начала координат и точку, координаты которой численно равны соответствующим элементам вектора. В случае вектора оператор Determinant (Определитель) является оператором модуля вектора, на что следует указать в его контекстном меню, выбрав пункт Absolute Value (Абсолютная величина). Модуль вектора может быть вычислен и символически. Пример 3.21. Модуль вектора 4 is. 6.481 у 3.2.7. Векторное произведение Векторным произведением (Cross Product), по определению, называется вектор, дли на которого равна произведению длин исходных векторов и синуса угла между ними, а направление его совпадает с направлением перпендикуляра к плоскости этих двух векторов (по правилу «буравчика»). Символически векторное произведение находится как определитель следующей матрицы (для случаев векторов в трехмерном пространстве):
где 1, j, к — единичные, взаимно перпендикулярные векторы, xl, к2, хЗ, у!,у2, уЗ - координаты (элементы) перемножаемых векторов. Обозначается векторное произведение в Mathcad символом «х» (соответствует принятому в математике и физике). Ввести оператор векторного произведения можно либо с панели Matrix (Матричные) (кнопка Cross Product), либо сочетанием клавши Ctrl+8. Пример 3.22. Сила F = (1, -3, -4 приложена в точке А(3, 4, 5). Найти величину и направляющие косинусы момента этой силы относительно точки В(1, 6, 9) F:= -3 А := 4 (Л В:= 8 Момент силы относительно точки В вычисляется как векторное Произведение a-F, где а — вектор, направленный к точке приложения силы: А-В 4 Величина момента силы определяется как модуль вектора a-F: [ix F -6 Направляющие косинусы момента силы (косинусы углов а, р, у, образованных вектором с осями координат) вычисляются как отношения соответггвужшик координат вектора к его длине; ( 2 cos ару ах F UxFl cos арЧ 3 2 3 ] ij Чтобы отобразить результат в виде простых дробей, выполните на нем двойной щелчок. В открывшемся окне Result Format (Формат результата) перейдите на вкладку Number Format (Формат чисел), в меню Format (Формат) выберггге пункт Fraction (Дробь), Векторное произведение вычисляется системой Mathcad и символически: к*/ «у \1г) fly . ----4-z у г z - I х 2-z-х----2 г V 2-х-у 3.2.8. Скалярное произведение векторов Скалярным произведением (Vector inner product) векторов называется число (или выражение), равное произведению длин перемножаемых векторов и косинуса утла между ними. Иначе скалярное произведение можно найти, сложив попарно перемноженные координаты (элементы) векторов. Скалярное произведение в математике принято обозначать символом •-». Аналогично оно представляется и в Mathcad. Чтобы перемножить скалярно лил некторч. можно либо пое пользоваться специальной кнопкой Dot Product панели Matrix (Матричные), либо просто «вести с клавиатуры оператор умножения (**•) Пример 3.23. Дан треугольник с вершинами А(1, 0, -5), В(-1, 1, -4), С(2, -5, -1). Найти внешний угол j при вершине В (рис. 3.5) А( 1.0,-5) 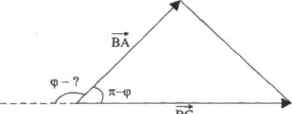 В(-1,1.-4)0(2,-5,1) Рис. 3.5. Чертеж к. задаче о нахождении внешнего угла треугольника Задаем точки треугольника в векторной форме: А := Г 1> [I НУ В: 1 С:= (2Л -5 Пользуясь определением скалярного произведения векторов, вычислим косинус угла ZABC, образованного сторонами треугольника — векторами ВЛ и ВС. Затем с помощью встроенной функции асо» (ярккосинус) определим величину внутреннего угла. Тал как суиша смежных углов равна 180". внешний угол найдем как ралмш ib п - ZABC Г(А-:= п - acos-- В) (С-В) П.А-В-С-В Скалярное произведете можно вычислить и символьно о —* - к 3 :-(х-у) + 2— + z-(z - 4) 3.2.9. Обратная матрица Матрица А" называется обратной к матрице А, если A-A -A~LA-E, где Е — единичная матрица (матрица, у которой элементы главной диагонали равны I, а все остальные — 0). Матрица имеет обратную только в том случае, если она квадратная и ее определитель не равен 0. Определение обратной матрицы — одна из основных задач матричной алгебры, поскольку в подавляющем большинстве доказательств и выводов этого раздела математики (имеющего огромное практическое значение) обратную 0 ... 31 32 33 34 35 36 37 ... 177 |












