Раздел: Документация
0 ... 74 75 76 77 78 79 80 ... 177 □ trig (Тригонометрические). Парметр или переменная рассматривается как тригонометрическая величина- На практике используется редко, так как реальна практически ни на что не влияет. Итак, попробуем найти корень из квадрата переменной, указав, что она принимает только действительные значения: Функция signum является функцией знака действительного числа Она возвращает -1 — если число отрицательно, 1 — если оно положительно — и 0 — если оно равно 0. Нетрудно заметить, что signum(x) х есть не что иное, как модуль х. Если известно, что переменная может быть только положительной или только отрицательной, можно придти к еще более простому результату. Для этого область изменения х должна быть указана в правом маркере оператора assume с помощью соответствующих неравенств: Если переменная изменяется в какой-то ограниченной области, то наиболее аффективно использовать модификатор RealRange: Не забывайте использовать оператор assume в тех случаях, в которых результат упрощения зависит от значения переменной (это прежде всего выражения с корнем, а также некоторые логарифмические выражении и выражения с модулем). Помимо оператор simplify, оператор assume часто применяется с операторами взятия определенного и неопределенного интегралов. Пожалуй, по логической нагруженности оператор simplify занимает первое место среди остальных символьных операторов. Действительно, ведь зачастую очень трудно четко определить, какое из двух выражений более простое, а следовательно, н задаться верным направлением в упрощении. Например, какое выражение проще: stn(2-x) или 2sin(x)-cos(T)V Очевидно, что ответ зависит только от особенностей решаемой задачи. Но Mathcad эти особенности не известны! И это, увы. не может не сказываться на качестве работы оператора simplify: упростить в Mathcad можно лишь наиболее простые, как правило, алгебраические или логарифмические, выражения. Так, из 10 первых примеров поданной теме из известного задачника Сканави оператором simplify правильно не был упрощен ни один! Л ведь это совсем несложные задачи, которые решают школьники в 6 классе. И если алгебраические выражения хотя бы в наиболее простых случаях могут быть успешно упрощены оператором simplify, то тригонометрическое выражение не будет правильно преобразовано почти наверняка (в лучшем случае система ограничится приведением подобных и упрощением, исходя из основного тригонометрического равенства sin1(j:)+coaJ(jf)~ 1 ) Эффективность упрощения алгебраических выражений очень сильно зависит оттого, есть ли н них корки и каким образом они заданы. Выражения, содержащие корни, упрощаются очень плохо, даже если и имеют простой вид. assume, х Real Range (3,5) si rnplify -* x Пример 7.14. Неэффективное упрощение выражений х- I simplify —* x-l Неверно, Правильный ответ sio(2x) 2cos(x) simplify -» - 1sin(2-x) 2cos(x) Неверно. Правильный ответ — sin(x). Глядя з 11\ приведенные примеры, трудна НС ил.кип.ся С у i Веред** нем ЧТО ОПера пня символьного упрощения выражений — это одно из самых слабых мест системы Mathcad. Впрочем, для этого есть вполне объективные и пока трудноразрешимые причины (увы, но компьютеры не умеют мыслить — они лишь очень быстро считают). Поэтому не стоит требовать от программы невозможное, и если вам понадобится решить пример из того же задачника Скаиавн, пока вам придется сделать это самостоятельно. Вернее, самостоятельно вам придется продумать стратегию упрощения. Mathcad же выполнит за вас вычислительную работу. Продемонстрируем данный подход на примере. Пример 7.15. Упрощение сложного алгебраического выражения Пусть нам необходимо упростить громоздкое алгебраическое выражение аила Оперировать столь большим выражением довольно непросто, Поэтому разделим его натри части и булсм проводить упрощение поэтапно. Очевидно, что в первую очередь нужно раскрыть квадраты в числителе первой части выражения: Раскрыв квадраты в числителе, обнаруживаем, что полученная дробь Может быть довольно легко ynpoutena. Однако оператор simplify *»е ладит» с корнями и дробными степенями. Поэтому, чтобы от них избавиться, выполним замену m-х1, и—у1. Чтобы в отлете *не всплыли*- функции csgn И signum, указываем, что хну могут был. только положительными (это соответствует истине, так как в исходном выражении имеются корни четвертой степени из m и п). 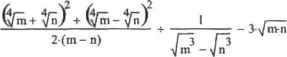 1 I 2-гл + 2П 2(т - п) 2 subsntute,m=x ,п = у assume,х & 0,у £ О simplify х-у Заменяем щ и пив х н у ао второ!) част» исходного выражения, а затем упрощаем его совместно 0 преобрагюванппй первой частью: I.2 2 substitute , m = х , n = у ] Г~з П d Ш - п I х-у 1 ± \2 у ,ч2 assume,х£ 0,у £ 0 2 ...-> X + *у -1- у simplify (xO-G6) Выполнив .чамспу, подставляем и выражение третью часть н проводим упрощение: х2 + х-у + у2 - 3\/тп substitute, т = х2, п = у2 assume,х£ 0,у 2: 0 * simplify х - 2-х-у + у Разлагаем полученное выражение на множители и возвращаемся к исходным переменным: 22 х - 2-х-у + у - и factor substitute, х = in, у = \/n Выражения, содержащие функции (логарифмы, тригонометрические), обычно упрощаются довольно плохо. Однако очень часто эффективность упрощения можно резко увеличить, сведя посредством замен выражение к чисто алгебраическому виду. Максимально упростив его алгебраическимн приемами, уже будет проще действовать,опираясь на специфические свойства входящих в неги функций. Для примера покажем, как можно с помощью Mathcad упростить логарифмическое выражение. При упрощении логарифмических выражений имеется две сложности. Во-первых, для задании логарифма от х по основанию а в Mathcad служит функция log(a,x). Однако в математике такие логарифмы принято обозначать с использованием нижнего индекса: logn(x). Если вид решения важен, то можно создать собственную функцию логарифма по некоторому основанию. Ед и нет вен пая тонкость здесь заключается в том, как ввести в имя нижний индекс (естественно, что использовать оператор извлечения элементов из матрицы нельзя). А сделать это очень просто, нажав клавишу (точка). Во-вторых, зачастую символьный процессор выдает неприемлемый результат по причине того, что все логарифмы он 1греобраэует в отношения натуральных. Избежать этого никак нельзя. Поэтому, если в ответ должны входить десятичные логарифмы или ло- ;[[щфмы пч основанию а. то соответствующее преобразование ответа придется проделать самостоятельно. Пример 7.16. Упрощенна логарифмических выражений Пусть нам необходимо упростить логарифмическое выражение следующего вида: 0 ... 74 75 76 77 78 79 80 ... 177 |












