Раздел: Документация
0 ... 84 85 86 87 88 89 90 ... 177 или Ньютона (о них мы поговорим чуть ниже) являются локально сходящимися. Это означает, что то, сойдется метод к решению или нет, очень сильно зависит от выбора начального приближения. В этом они уступают глобально сходящимся методам. Скорость же сходимости лучших методов интервалов локализации корня вроде метода Риддера или метода Б рента близка к скорости сходимости метола секущих и лишь немного уступает скорости сходимости метода Мюллера. Поэтому, если корень не имеет особенностей, для его определения лучше использовать метод Риддера или метод Б рента. Однако есть несколько ситуаций, в которых от использования методов интервалов локализации корня лучше отказаться. Во-первых, корню может соответствовать не пересечение функцией оси X, а лишь ее касание. Во-вторых, таким образом нельзя определять комплексные корни. В-трстьнх. методы вроде метода Больцано неудобно использовать, если процесс решения уравнения является частью более сложной вычислительной схемы, реализованной в виде программы. Во всех этих случаях лучше применять методы, отличительной особенностью которых является то, что они основываются на приближении к корню, а не на интервале его локализации. Этим методам соответствует другая форма функции root, имеющая только два аргумента (имя функции и переменной). Приближение к корню присваивается переменной выше функции root (см. пример 8,13). Пример в. 13. Численное решение уравнения при наличии точки приближения к корню Задаем функцию, описывающую уравнение, и находим точное значение первого положительного корня. f(x) :=cos(2x + I) cos(2x + l) = 0aolve,X+ --я— + --я Qoal,20 -» .285398163397448309 2 42 4 Задаем начальное приближение и ищем корень при различных значениях TOL х:=0.2 TOL:= 10" Sroot(trx),x) - 0.285394105343086 TOL:= ЦТ 10root(f(x).x) = 0285398163399349 Функция root с двумя аргументами по умолчанию ишет корни посредством метода секущих. Если этот метод не сходится за определенное количество итераций к решению, применяется метод Мюллера. О сути этих методов мы поговорим чуть позже. Крупным преимуществом метода секущих и метода Мюллера является то, что с их помощью можно находить комплексные корни. Обязательным условием при этом является го, что приближение также должно быть комплексным (см. пример 8.14). Пример 8.14. Численное определение комплексных корней 2 fl[x) :=х + х+ 1 solve,х L5000+ .8660i\rl:«-4+7ii2:=-4-7-i float,4-KL.5000-.8660iJ rool(jTrl),rI) =4).5+0.866i toot(f(r2),r2) = -OJ-O.8661 Кстати, довольно часто бывает так, что, основываясь на действительном приближении, функция root находит комплексный корень. Это связано с тем, что в Mathcad все числа рассматриваются как комплексные. При использовании метода секущих н метода Мюллера появляются дополнительные сложности, которых нет при применении методов интервалов локализации корня, Так, при наличии у уравнения нескольких корней бывает проблематично так подобрать приближение, чтобы был найден именно нужный корень. Причина - при этом не работает, казалось бы, очевидное правило, что определяться должен тот корень, который ближе к точке приближения. Это правило справедливо лишь, если точка приближения находится в окрестности корня. Иначе то, какой корень будет найден, будет зависеть в первую очередь от особенностей поведения функции. Решение этой проблемы простое: приближение нужно не «братье потолка», а определять по графику. Во-вторых, корень уравнения методом секущих (Мюллера) может быть не найден, если начальное приближение было задано в районе экстремума или разрыва, а также в области, в которой кривая функции имеет очень маленький наклон. Пример 8,16. Поиск корня уравнения при разных приближениях Первый положительный корень уравнения, описываемого следующей функцией, равен я/3: fl[x) :>=coe(3x)5 + 1 f)"° j = 1.04719755И966 То, как ведет себя функция в области корня, показано на рис. 8.6. Если в качестве приближения к корню взять точку к-0 (экстремум), то численный метод к решению не сойдется. Приближение, очень близкое к экстремуму, также ие приведет к положительному результату. Ближайшая к экстремуму точка, при использовании которой в качестве приближения функция root найдет корень, это х-0,001. Однако определенный при атом корень будет расположен очень далеко от искомого корня х-я/3: ж;-0.00] root(f(x),x) = 114.144104502797 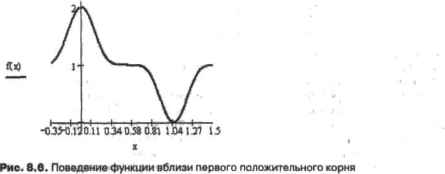 Большинство точек в области от 0.001 до 0.1 прн использовании их в качестве приближения к корню или не дадут сходящейся к решению последовательности, или эта последовательность будет сходиться к удаленному корню. Лишь отдельные точки дадут верное решение. Большая часть точек в области от 0,1 до 0.3 дадут верное решение. Это связано с тем, что кривая функции в этом интервале имеет достаточный наклон по направлению к корню. Однако часть точек будут давать иди не сходящуюся последовательность, или последовательность, сходящуюся к удаленному корню. х:=0.1гооцЭД.х) = 1.04761194953047 х := 0.22 root{fltx), х) = -8.00373139717741 xl О3 В области от 0.3 до 0.8 почти вес точки дают последовательность, не сходящуюся к корню. Отдельные точки приводят к решению, однако выдаваемые прн этом корки очень далеки от ft/3. Дапные сложности обусловлены тем, что кривая в интервале (0.3,0.8) почти горизонтальна *:-0.57 rootftiM =-3.00231601851947xl(? Все точки итгтервяла (ОД п/З), взятые в качестве при&чижения к корню, дают сходящуюся к необходимому корню последовательность. Это связано с тем, что данная область непосредственно прилегает к корню, а также с тем. что соответствующий еН участок кривой имеет хороший наклон и лишен экстремумов и разрывов. х;=0.9тлЩх).х) = 1.0467392869927 Область кривой справа от корня симметрична области слева. Поэтому с точки зрения выбора приближений они идентичны. Пример 8.15 показывает, сколь сильно то, даст ли приближение сходящуюся к нужному корню последовательность или нет, зависит от особенностей поведения функции. То, почему так происходит, вы поймете, когда мы разберем принципы метода секущих и метода Мюллера. В отличие от методов интервалов локализации корня, методы секущих и Мюллера склонны находить корни там. где их нет. Такие корни называются ложными. Пример в. 16. Неверное решение уравнения методом секущих Попытаемся решить уравнение, заведомо ие имеющее корней — е~*-0. Система находит корень. Причем, его величина резко увеличивается с уменьшением TOL. f(x):=e~* х:=1 TQL:= 10~ 5root(fi;x),x) = 11.625 TOL:=10~ 12root(3x),x) =28.26 Приведенный пример показывает, насколько «глупой» может быть функция root Попробуем разобраться, в чем же причина возникших трудностей и как можно избежать ошибок. На самом деле, все просто: как вы помните, критерий сходимости к корню у функции root — это I f(rq) <TOL Функция же е" имеет одно очень вредное свойство: бесконечно близко приближаться к оси X, никогда ее не достигая. Из этого следует, что если в какой-то точке rq выполняется условие I f(rn)l <ТОитоонобудетсправедливоддя всех точек, лежащих правее га Л точек таких бесконечно много! Избежать же обнаружения ложных корней очень часто можно, введя дополнительно, в качестве критерия сходимости к корню, условие близости двух последтюс приближений го—гп , <T0L. Увы, но функция root этого не делает. Чтобы не ДОЙТИ корень там, где функция просто сближается с осью X, опять же нужно строить график. Вообще, действовать вслепую, численно решая уравнения, ни в коем случае нельзя. В общем, шанс получить ошибочный с/твет при использовании метода секущих (или Мюллера) очень велик. Как же этого избежать? В первую очередь, для этого нужно 0 ... 84 85 86 87 88 89 90 ... 177 |












