Раздел: Документация

0 ... 82 83 84 85 86 87 88 ... 177

метлы группы основаны на той же основной идее, однако они используют разного рода хитрые приемы, увеличивающие скорость сходимости алгоритма, Поэтому есть смысл рассмотреть сначала метод Больцано в его классическом варианте, а затем обсудить открытые Риддером и Брентом улучшения.

Алгоритм метода Больцано следующий.

1,Задается функция, нули которой необходимо найти. Определяется интервал ота0 до it... на котором локализован корень. На то, что корень находится именно па этом интервале, будет указывать то, что функция иа чт фаницах принимает значения разных знаков. Этот признак будет работать, если функция непрерывна на промежутке [аа bа также если корень не является корнем типа касания.

2,Определяется координата середины интервала [л0 bj се.

3,Проверяется, в какой из фаниц интервала функция принимает противоположный знак тому знаку, который она имеет в средней точке. Тут возможны три варианта.

•Если f(a0) и f(c0) имеют разные знаки, то корень находится на промежутке {а,,, с0. Значит, можно сузить интервал локализации, взяв в качестве его правой границы cD вместо bD.

•Если f(b0) и {(cj имеют разные знаки, то корень находится на интервале [с,, Ь Сужаем интервал, взяв в качестве левой границы св вместо а,.

•Если с0-0, то является искомой точкой корня. Возвращаем ее как результат.

4 Повторяем описанные выше действия до тех пор, пока длина интервала ав, bj не уменьшится до 2-T0L При этом, если взять в качестве приближения к корню среднюю точку интервала, пофешность не превысит TOL Узнать же, сколько итераций должен совершить алгоритм, чтобы интервал локализации корня сузился до 2-ТГД. очень просто. На каждой итерации ширина интервала уменьшается в два раза. Исходя из этого можно записать следующее неравенство (здесь N — необходимое количество итераций):

Ь - а

- 5 2TOL

2N

Решив данное элементарное неравенство, получим:

n, 1п№ - а) - ЦТОЦ Ln(2)

Таким образом, точность поиска корней методом Больцано не зависит от особенностей функции, а определяется только количеством итераций.

Крупным недостатком метода Больцано является его медленная сходимость. Так, к примеру, чтобы найти корень с точностью до 0.00001 при ширине интервала 10, необходима 21 итерация. Это довольно много. Существуют методы, в которых проблема медленной сходимости метода Больцано решается за счет того, что учитываются особенности поведения функции. Это метод ложного положения, а также используемые в Mathcad методы Риддерл н Б рента. Увы. но в случае этих методов уже нельзя однозначно оценить, сколько необходимо итераций для достижения требуемой точности приближения корня. Поэтому в качестве критериев сходимости используются величина функции в точке последнего приближения и (или) разность двух последних приближений. Чтобы вам было проще разобраться в сути метода Больцано, приведем его реализацию на языке профаммирования Mathcad:

---

Bolcano(f,a,b,TOL) :=

em>r(Bad interval!") if

v f(a) = 0v iTb) = 0

Щ I Kb)

N «- floor

in(b - a) - InfTOU ln(2)

for i e 1.. N + 1

с «- (a + b) + 2

return с if i = N+ 1

return с if flc) = 0

с if т*Т

a «- с otherwise

Проверка показывает, что функция Bolcano работает ничуть не хуже функции root:

Bolcano(f,l,4,10 )=1.ООО0ОО1О371853тс BoLcancJf, 1,4,10 )=1.0000000000122бп;

В приведенной реализации метола Больцано есть несколько технических моментов, на которые нужно обратить ннимание.

□Ключевым шагом метода Больцано является определение того, принимает функция в двух точках значения одного или разных знаков. Чтобы это выяснить, разделим значение функции в точке на модуль этого значения. В результате мы получшл 1 или -1, то есть, по сути, выделим знак. Проделав аналогичную операцию для второй точки и сравнив полученные значения, мы узнаем, имеется ли на промежутке корень. Выделить знак числа также можно, используя встроенную функцию Mathcad sign,

□Определяя количество необходимых для достижения требуемой точности итераций но выведенной выше формуле, результат необходимо округлить до ближайшего меньшего целого числа (подумайте, почему). Выполняет эту операцию функция floor. Соответственно, округление до ближайшего большего целого числа производит функция ceil.

□Перед тем как запустить работу алгоритма Больцано, нужно проверить, принимает ли функция на концах интервала значения разных знаков. Если это не так, останавливаем работу кода и возвращаем сообщение об ошибке посредством функции error.

Метод Больцано имеет важное историческое и теоретическое значение, однако на практике для решения уравнений он не используется. Причина — его медленная сходимость. То есть, чтобы получить посредством него решение нужной точности, следует проделать значительный объем вычислительной работы. Существует несколько методов, которые, используя ту же основную идею, что и метод Больцано, обладают лучшей сходимостью. Наиболее простой из них — метод ложного положения (Reguia Falsi).

Отличие метода ложного положения от метода Больцано заключается в том, как вычисляется очередное приближение. В методе Больцано для этого находится среднее арифметическое границ интервала локализации корня: cn=(an+bn)/2. В методе ложного положения через точки (а, f(an)) и (Ьл, f(bn)) проводится секущая (рис, 8,5). Точкой

Цх) := sin(x)

---

с , в которой секущая пересекает ось X, заменяют одну из границ интервала локализации корня, сужая его. Приближение считается достаточно точным, если I f<cB)i <T0L и (или) c-cJ <T0L (простой формулы, позволяющей определить, сколько необходимо итераций для достижения требуемой точности, в случае метода ложного положения, в отличие от метода Больцано, нет).

Рис. 8.6. Иллюстраций метода ложного положения. Неплохая точность достигается уже на второй итерации

Метод ложного положения сходится быстрее метода Больцано, но есть и более эффективные методы. По умолчанию функция root применяет метод Риддера. Основное улучшение в нем, по сравнению с методом Regula Falsi, довольно простое, и основано оно на распространенном втеории численных методов приеме — использовании интерполирующего функцию полинома (точно так же осуществляется, например, переход от метода секущих к методу Мюллера, от метода трапеций - к методу Симпсона, от метода Эйлера — к методу Рунге-Кутта). Если налагать суть метода Риддера в деталях, то на каждой итерации пподелываются следующие шаги. Сначала вычисляется значение функции в средней точке интервала с -(а +Ь )/2, Затем через имеющиеся три точки (граничные точки интервала и средняя точка) проводится интерполирующая функцию парабола. Так как через К точек проходит только один полином степени К-1 (попробуйте это доказать), то интерполирующая парабола будет уникальной. Несложно вывести, что данная парабола будет определяться следующей функцией (подобный вывод приводится в гл. 10 при рассмотрении метода Симпсона):

Если интервал (ae, bj достаточно узок, то поведение интерполирующей параболы будет весьма схоже с поведением функции. Поэтому логично в качестве приближения к корню использовать точку, в которой парабола пересекает ось X. Найти эту точку несложно, положив Рч(х)-0 и решив полученное квадратное уравнение. В результате будет получено два корня, однако только один из них будет принадлежать интервалу (ал, \< ) Риддервывел формулу, которая дает возможность сразу вычислить нужный корень (при ее выводе считалось, что уравнение задано не относительно переменной х, а относительно экспоненциальной величины eQ). Данная формула имеет Вид: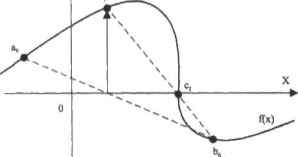

PBW=fa)Jt2-2f(cn>x+fW

0 ... 82 83 84 85 86 87 88 ... 177