Раздел: Документация
0 ... 80 81 82 83 84 85 86 ... 177 В основе всех численных методов решения уравнений лежит принцип подбора. Но, в отличие от подбора возможных корней человеком, в численных методах этот процесс является строго направленным. Основным понятием численных методов является итерация. Итерация — это, буквально, «повторение», то есть все численные методы решения уравнений построены на принципе повторения одного и того же действия или последовательности действий, результатом которых является большее или меньшее приближение некоторого промежуточного значения переменной к корню. Поэтому численные методы решения уравнений называются еще итерационными. Количество необходимых итераций определяется скоростью сходимости алгоритма (эффективностью) и особенностями уравнения, Эффективность различных численных алгоритмов может различаться весьма значительно, но это не значит, что всегда стоит избирать из них наиболее быстрый: чем выше скорость сходимости к решению, тем, как правило, выше чувствительность алгоритма к разного рода трудностям (многочисленным экстремумам, разрывам илн недифференцируемости в некоторых точках). Для численного поиска решений уравнений с одним неизвестным в Mathcad существует специальная встроенная функция root (с англ, - корень). Функция эта может использоваться в двух различных формах, при этом реализуются разные численные алгоритмы. Так, если определена только одна точка приближения к корню, поиск решений будет осуществляться так называемым методом секущих (или, в случае неудачи использования метода секущих, его более эффективной модификацией — методом Мюллера (Muller)). Если же задан интервал, на котором предположительно локализовано решение, то поиск его будет осуществлен с применением двух модификаций метода Больцаио деления пополам (метода бисекции) - методов Риддера (Ridder) и Брен-та (Brent). Идеи всех этих методов, их достоинства и слабые места мы подробно обсудим в этом разделе. Если необходимо найти корень некоторого уравнения, причем известен интервал, в котором он локализован, проще всего использовать функцию root с четырьмя аргументами: rcot(f(x)AaJj), где f{x) — функция, определяющая уравнение, х — переменная, а н b - границы интервала локализации. Обязательным условием является то, что значения функции на концах интервала должны быть противоположных знаков. Это связано с особенностью используемых root алгоритмов. Если нарушить это условие, система выдаст сообщение об ошибке. Также функция f(x) должна быть ограниченной и непрерывной на промежутке (а, Ь). Если же она имеет точку разрыва на этом промежутке, то численный метод может не сойтись. Пример в.10. Численное решение уравнения при известном интервале локализации корня Попробуем протестировать функцию root и для. этого ни Идем корни какого-нибудь уравнения, точное решение которого очевидно. К примеру, возьмем уравнение все корни которого имеют вид */<(+(n/2)xN (Ne R, где R— множество целых чисел). Попробуем найти первое положительное решение. Очевидно, что таковым будет х-тг/4 (что очень хоровго видно на рис. 8.3). Посмотрим, однако, найдет ли атот корень функция root, Интервал локализации определим от 0 до в/3: root Г(\),х 0.25 л 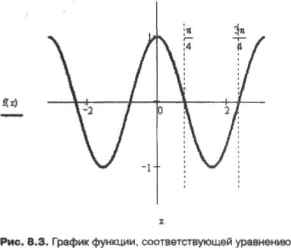 Программа не подвела: решение кайлено в точности. Попробуем решить это уравнение с другим интервалом локализации: В приведенном выше примере при использовании второго интервала приближения полученный результат отличается от решения для первого интервала, хотя корень х-0.25я принадлежит обоим интервалам Все дело в том, что и этом же промежутке находится еще один корень, и заранее предсказать, какой именно из них будет выдан в качестве ответа, .эдтрудттительно. Поэтому следует ввести еще одно ограничение для применения функции root в рассматриваемой форме: на промежутке должен быть локализован только один корень, В тех случаях, когда определить границы такой локализации невозможно, следует применять функцию root с одной точкой приближения (то есть перейти от методов интервалов локализации корня к методам, основанным на методе секущих). Хотя практически всегда определить нужный промежуток можно и чисто визуально, ггредварительно построив график Вообще, строить график всегда желательно, когда вы используете численные методы: это самый надежный способ избежать ошибок и не потерять корни. Очень важной характеристикой решения является его точность. В Mathcad можно регулировать величину погрешности решения, изменяя значение специальной системной переменной T0L (от англ. tolerance — точность). В общем случае, чем меньше T0L, тем точнее будет найден корень, но и тем больше времени уйдет па его определение (а также будет выше риск, что численный метод не сойдется к решению), Строго говоря, TOL — это параметр, количественно определяющий условия прекращения итераций. Судить о том, что численный метод сошелся к решению, можно по двум критериям. Во-первых, можно реализовать численный метод так, что цикл алгоритма остановит свою работу и выдаст последнее значение приближения к корню ро, если f(P„) примет значение, меньшее по модулю, чем T0L Во-вторых, можно считать, что достаточная точность уже достигнута, если два послед гих приближения различаются на величину, по абсолютному значению меньшую TDUl Pn-p„.l <Т01 Какой из подходов лучше? По большому счету, они равнозначны. Если используется критерий I f(pn)l <T0L, то решение будет локализовано в горизонтальной области, ограниченной параллельными dch X прямыми (x)=T0L Blow(x)—-TOL (рис. 8.4). Если функция изменяется быстро, то она пересечет границы области достаточно близко от корня. Это гарантирует то, что точность приближения к корню будет хорошей. Однако если функция изменяется очень медленно, может оказаться так, что точка, выданная как приближение к корню, реально располагается очень далеко от него (см. нижнюю часть кривой на рис. 8,4).
Рис. 8.4. Геометрическая интерпретации TOL Если в качестве критерия сходимости численного метода используется модуль разности двух последних приближений, то решение будет находиться в вертикальной области, ограниченной параллельными оси Y прямыми с абсциссами г-а и г+Ь, где г — истинная координата корня. Численно найти а и Ь непросто, но можно, если знать, какой алгоритм по отношению к какой функции используется. Рассматриваемый критерий хорош, если функция вблизи корня изменяется относительно медленно. Если же она изменяется очень быстро, то может оказаться так, что найденному решению будет соответствовать очень большое значение функции, которое даже с учетом округления не удовлетворит обязательному условию существования корня f(r)-0 (см. верхнюю часть кривой на рис. 8.4). Важно отметить то, что а н Ь вполне могут оказаться больше T0L. так как разность двух последних приближений и расстояние от них до корня прямо никак не связаны. Если алгоритм сходится медлсшю (по причине своей неэффективности или «неудобности» функции). TD расстояние между точками двух последних приближений может быть весьма малым даже тогда, когда они находятся еще очень далеко от корня. 0 ... 80 81 82 83 84 85 86 ... 177 |
||||||||||||||||||||||||||||












