Раздел: Документация
0 ... 79 80 81 82 83 84 85 ... 177 substitute, х— float.3 512 7K125 -20 + 10i-62, ь 788 26 . ,2 У, 5 5 13.5+6.231 Проверка по графику показывает, что х-1 это не единственный корень уравнении. Также корнем, вероятно, является (рис. 8.1). 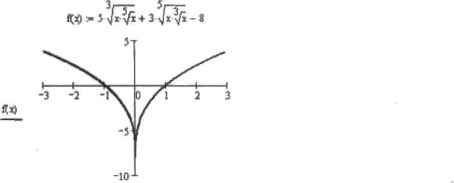 х Рис. В. 1. Соответствующая уравнению функция четная {то есть ее участок правее оси Y является зеркальным отображением участка, лежащего левее данной оси). Это означает, что у корня х=1 будет парный корень х*-1 Можно лн преобразовать решаемое уравнение так, чтобы символьный процессор с ним справился? Сложность данного уравнения заключается в его иррациональности. Mathcad довольно плохо оперирует с выражениями, содержащими корни и дробные степени, поэтому от них нужно стремиться избавляться. Для этого нужно найти такую замену, которая сделала бы иррациональное выражение рациональным (или хотя бы упростила его). В нашем случи хорошей заменой будет к— 15 I S-i/*\fx+ 3-Jx-x- 8 substitute.x=t 2 -> 5-[ \t 2 J
- 8 Полученное в результате замены выражение следует уггроеппъ вручную, тис как оператор simplify (даже в сочетании с assume) с этой задачей не справится (вероятно, из-за слишком большого количества степеней). 15 б 1 ------> з 2 5 3 15 4 1 ------> 2 2 3 5 3 2 5-Г + 3-1 -8 В результате замены мы получили простое алгебраическое уравнение третьей степени, которое Mathcad легко решит. { I - 3 2 St + 3-t - В solve,! -» 1 -4 г. л — + --1-6 5 5 -* г.,г ----1-6 V 5 5 & Ограничившись действительным корнем, находим, при каких х переметшая t принимает значение 1. г х = 1 solve,х —> Найдешгые корни ссютветствуют правильному решет по уравнении. Задача 3. Решить показательное уравнение следующего вида: (2+/зГЧ(2/1- 4 2-3 Оператор solve способен решить данное уравнение, но лишь приблизительно (корни выдаются в формате чисел с плавающей точкой): -2х+1 х2-2х-1 2-3 solve, х 0 То, что оператор solve определял корень только приблизительно — это не беда, так как он имеет целочисленное значение. Хуже другое. Проверка по графику показывает, что у уравнения должно быть три корня, а не один (рис. 8.2). 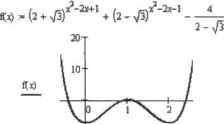 i Рис. в.2. Кривая дважды пересекает осьХ, а в точке х=1 касается ее. Таким образом, у уравнения будет три корня. Так как кривая симметрична относительно прямой х=1, два корня будут сопряжены и будут иметь вид t+a и 1-а, где а — некоторое число Чтобы упростить уравнение, используем тот факт, что подстеленные выражения в new являются сопряженными н поэтому их перемножение ласт целое число: Отси u.i. (2 + \/з)(2 - sfi) expand-* 1 2-v/l=—l— 2+ n/3 Используя данное равенство, так преобразуем уравнение, чтобы в нем был только один вид под-степенного выражения. Упрощенное таким образом уравнение оператор solve без проблем решит (2 < V3? 2Х+ + (2 - чГэГ2 = 2 -V3 substitute,2-i/3 solve,х simplify 2 + >/3 ( i 22+ Если, несмотря на все ухищрения, аналитически решить уравнение не удастся, следует попытаться найти его решения хотя бы численно. Как это сделать, подробно описывается в следующем разделе. 8.1.2. Численное решение уравнений Далеко не все уравнения можно решить аналитически. Это можно сделать лишь в случае отдельных, «удобных» уравнений. На практике же приходится работать с уравнениями, включающими разнородные функции (что, как правило, автоматически означает невозможность символьного решения) или с очень неудобными коэффициентами. Справиться со многими из них привычным преобразованием или заменами никак не получится. Что же делать г Естественно, если вам попадется такое «нерешасмое» уравнение, вы попытаетесь просто подобрать корни. Для этого вы будете подставлять какне-то значения переменной (выбор которых, скорее всего, в основном будет определяться вашей интуицией) в надежде на то, что какое-то из них обратит уравнение в нуль. К сожалению, такой способ весьма малоэффективен на практике: подставив десяток-другой значений, вы, почти наверняка, предпочтете удовлетвориться мыслью о том, что данное уравнение не имеет решений вовсе, чем продолжать эту чрезвычайно неинтересную работу. Но если у вас есть компьютер с системой Maihcad, то никаких проблем с поиском решения не будет, вне зависимости от сложности уравнения. Конечно, аналитическое решение компьютер НС всегда найдет даже для очень простых уравнений (в этом пока человек значительно превосходит машину), но зато, ввиду колоссальной, по сравнению с человеческой, скоростью обработки данных, очень эффективными становятся так называемые численные методы. 0 ... 79 80 81 82 83 84 85 ... 177 |












