Раздел: Документация
0 ... 85 86 87 88 89 90 91 ... 177 понимать, как именно функция root ищет корни. Разберем для начала более простой метод секущих. Он заключается в следующих шагах. □В качестве первой точки приближения х, определяется начальное приближение, вводимое пользователем, □Точка второго приближения Xj определяется как сумма первого приближения и величины, равной заданной точности; ххТГД., □Через точки (х f(xt)) и(хг, f(x) проводится секущая. Абсцисса точки (r, f(r)), в которой она пересекает ось X, определяется как третье приближение х. Найти х, несложно. Для этого нужно записать уравнение прямой, проходящей через точки (ж-. f(x,)) и (Xj.ftXj)), приравнять его нулю и выразить х. В результате получим следующую формулу: <*2)(*2-*1) □Если значение функции в точке третьего приближения удовлетворяет критериям сходимости к корню, то эта точка определяется как корень. В противном случае соответственно точкам третьего н второго приближения проводится еще одна секущая, которая дает четвертое приближение. Процесс повторяется до тех пор, пока полученная точка приближения не удовлетворит условию корня. В общем случае формула для получения приближения на основании двух предыдущих 1гриближе-ний будет иметь вид: *n=Vl~ <v.)-<v2) Метод секущих можно гораздо проще понять, если отобразить ход поиска корня на графике (рис. 8.7). v А 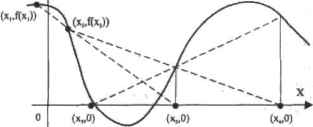 Рис. 8.7. Иллюстрация метода секущих. Приемлемое приближение определяется за три итерации Реализовать метод секущих самостоятельно, используя язык программирования Mathcad, проще простого. Однако нужно учесть, что. в отличие от глобально сходящихся методов интервалов локализации корня, метод секущих при неудачном выборе начального приближения может породить расходящуюся последовательность. Поэтому, если количество итераций превысит некоторый максимум (несколько десятков), работу программы нужно остановить и вывести сообщение об ошибке. Программу мы напишем так, чтобы в качестве результата она возвращала вектор из двух элементов. Первым элементом будет найденное решение, второй элемент будет содержать вектор со всеми &ЫЧНСЛС1ШЫМИ в ходе поиска корня приближениями. Анализируя, насколько быстро последовательность приближений сходится к корню, мы сможем оценить эффективность метода секущих. Secant(f,e,TOL) := while j р e + TOL lasi(p) Plasi(p)-I a <- p lastfp)-! ДЬНЬ-а) <T0LA<P1-«(P))I<TQL) ) еггот("Ооп1 converge to a.solution") if lasi(p) > 50 (pu«(p) 0 last(p) Профамма Secant несложна, но в ней есть моменты, которые стоит пояснить. □Приближения записываются в вектор р. Чтобы получить новое приближение, нужно подставить в формулу метода секущих значения последних двух приближений. Чтобы адресовать их, используем функцию last, возвращающую индекс последнего элемента в векторе, Также можно применить функцию length, определяющую количество элементов в векторе. □Итерации должны совершаться до тех пор, пока не выполнятся условия сходимости к корню. Добиться этого можно, внеся соответствующий комплекс условий в заголовок цикла while и выполнив над ним операцию логического отрицания посредством оператора ~м Решим с помощью функции Secant уравнение с известными корнями при разном значении T0L: 2(-Л f{x):=x -2х-3ft>) solve,х "Ч Secant(f.0.7,lCr5)=(-0.9999999999917tl {1 1,1») Secant(f,0.7110~*)={-1 {12,1)) Итак, метод секущих сходится весьма быстро. Если приближение выбрано достаточно близко к корню, то каждая итерация уточняет результат приблизительно на полторы значимые цифры. Если же первое приближение удалено от корня, то несколько итераций уйдет на то, чтобы метод «стал на верный курс*. Анализируя векторы приближений, возвращаемые функцией Secant, можно обнаружить, что скорость сходимости возрастает по мере продвижения к корню: Secant(f>4.104)0 j-з) =(l 1 0.17 0.03 1.28* 10"3 1.02* 10**3 3.28 х Ю~9) Т (Secant(f.~2,10~*)0 ,+j)=(-l -1 -0-167 -0.032 -1.28x10*"* -1.024x10-3 -3-275х10-9) Кстати, написанная нами программа превосходит root, с точки зрения надежности функции, что связано с тем, что мы используем два критерия сходимости к корню, a root — только один. Так, например, если мы попытаемся решить уравнение е~*=0 с использованием функции Secant, то будет выдано сообщение об ошибке: Dorrt convert to a solution. Функция же root в такой ситуации выдаст ложный корень (см, пример 8.16). Зная то, как работает метод секущих, легко понять, почему так важно правильно выбрать начальное приближение. □Начальное приближение должно быть достаточно близко к корню для того, чтобы первая секущая была направлена в его сторону (первая секущая, ввиду малости TQL, ведет себя практически так же, как касательная к точке начального приближения). Если между приближением и корнем имеется экстремум или разрыв, то направление функции в окрестности приближения может быть таким, что секущая «уйдет в сторону», □Если приближение находится близко к экстремуму, метод секущих может не сойтись или же будет получен корень, весьма удаленный от искомого. Это связано с тем, что вблизи экстремума кривая имеет очень малый наклон. Из-за этого малый наклон будет иметь и первая секущая. Соответственно точка, в которой она пересечет ось X, будет очень удалена от первого приближения. □Аналогично случаю с экстремумом, решение можно не получить также, если в окрестности первого приближения функция изменяется очень медленно (см, пример 8,15). □Возможны и более сложные случаи, в которых метод секущих не сойдется. К примеру, корень может соседствовать с бесконечным разрывом. В общем, подобрать подходящее начальное приближение для метода секущих может быть непросто. Поэтому его стоит использовать лишь в оговоренных выше особых случаях. В остальных случаях лучше ггрименять глобально сходящиеся методы интервалов локализации корня. Если функции root не удается найти решение посредством метода секущих, она пытается это сделать посредством более совершенного, но и сложного метода Мюллера. По сути, данный метод является модифицированным с целью увеличения скорости сходимости методом секущих. В этом методе секущая заменяется параболой. Соответственно, для построения этой параболы используются три последних приближения. Точка, в которой парабола пересекает ось X, считается новым приближением. Метод Мюллера сходится быстрее метода секущих, давая, в среднем, по две значимые цифры на одну итерацию. Однако он более чувствителен к начальному приближению и виду функции. 8.1.3. Определение корней полинома Одним из основных недостатков функции root является то, что одновременно она способна найти только один корень уравнения. Чтобы найти остальные, придется проделать те же операции, но для других приближений. В случае большого количества корней это может быть очень утомительно. Конечно, можно написать программу, выполняющую эту работу, — однако это слишком сложно для большинства пользователей, Но все значительно упрощается в том случае, если ваше уравнение представлено алгебраическим полиномом. Для этого частного случая разработаны очень эффективные алгоритмы решения, и использовать для поиска корней полинома, например, метод секущих было бы не совсем рационально. Поэтому совсем не удивительно, что в Mathcad существует специальная функция поиска решений полинома polyroots(V), где V — вектор, составленный из коэффициентов полинома. Важной особенностью задания V 0 ... 85 86 87 88 89 90 91 ... 177 |












