Раздел: Документация
0 ... 96 97 98 99 100 101 102 ... 177 8.2.3. Численное решение систем нелинейных уравнений Как и в случае одинарных уравнений, к численным методам решения системы уравнений следует обращаться тогдп. когда с ней не справится аналитический процессор Mathcad. Реально это приходится делать очень часто, так как лишь редкие системы нелинейных уравнений могут быть решены символьно. В Mathcad для численного решения систем уравнении служит блок Given-Find. Правила его задания схожи с правилами, использующимися при символьном решении систем уравнений, однако есть и особенности. Отметим их. □Аналогично численным методам решения уравнений с одним неизвестным, сначала следует определить начальные приближения. В случае систем уравнений приближение должно быть определено для каждой переменной. Например: x:=l(f3 у := 103 z:=I □Для вывода результата после функции find следует ввестиоператор численного вывода Используя блок Given-Find, можно решать системы, содержащие до 250 нелинейных уравнений и до 1000 линейных. Впрочем, на практике редко приходится встречаться с. такими огромными системами, чтобы можно было проверить эти данные. Однако замечено, что уже иа системах из 5-7 уравнений Given-Find начинает давать сбои. Поэтому к декларируемым в справочной системе возможностям (гужно относиться с долей скепсиса. Пример в.ЗО. Численное решение системы нелинейных уравнений х := 10 у := 5 Given yfx + \fy =9Vx + >/у = 5 findfjcy) = Редкое нелинейное уравнение имеет только один корень. Многие из них (периодические функции) могут иметь бесконечное множество решений, В случае же систем нелинейных уравнений ситуация еще более усложняется тем, что для большинства на них весьма проблематично определить начальные приближения И даже количество корней (доказательство их существования для систем с большим, чем 2, количеством уравнении - это задача очень сложная и часто не решаемая в случае нелинейных разнородных функции). С этими проблемами можно было очень просто справиться в случае уравнения с одним неизвестным, определяя нужные характеристики чисто визуально па графике. Аналогично можно поступить, в принципе, и для систем из двух уравнений, но лишь в тех редких случаях, когда одна переменная однозначно выражается через другую, Например, для системы х + у = I х2 - бу = 0 начальные приближения (и количество решений) действительно можно найти по де-каргоному графику, гак как каждое из уравнений может быть представлено кривой на плоскости (окружностью и параболой). Точки пересечен1И1 этих кривых — это и есть решения системы (рис. 8.10), 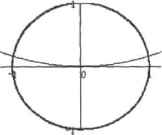 - Рис. 8.10. Определение начальных приближений для численного метода решения системы уравнений с помощью графика Но далеко не всегда можно представить каждое уравнение системы в виде функциональной зависимости одной переменной от остальных. В большинстве случаев разделение переменных невозможно. При этом единственный универсальный способ прикинуть приближения для системы на двух уравнений — это построить поверхности, представив каждое уравнение как функнню двух переменных. Однако точно определить Приближения по трехмерному графику довольно сложно (это можно сделать лишь очень и очень приблизительно). А если в системе 3 или 4 неизвестные? При этом, естественно, никаких графиков построить нельзя. В этом случае приближения нужно брать такие, чтобы они были близки к ожидаемому результату. Поиск же всех решений системы уравнений с помощью численного метода — это довольно сложная и трудоемкая задача. Обычно с ней справляются, решая систему для целой области приближений. Впрочем, если в системе только два уравнения, то очень часто приближения все же можно определить весьма точно. Для этого нужно построить график, на котором будут отображены кривые, получаемые прн пересечении соответствующих уравнениям поверхностей плоскостью X0Y. Чтобы нарисовать такие кривые, нужно так преобразовать функции, чтобы они принимали только два значения: одно, когда функция больше 0, И второе, когда она меньше 0. Затем на основании этих функций следует построить контурный график (рис 8.11). Если окажется, что Mathcad не сможет найти решения при данных приближениях, попробуйте сменить их на другие. Вполне вероятна такая ситуация, что корни существуют, однако численный метод, «подбираясь» к ним, «попал в капкан* разрыва или экстремума. При этом дальнейшее вычисление приближений окажется невозможным. Также довольно распространенной ошибкой является попытка поиска комплексных корней при действительных приближениях. Чтобы найти мнимые корни, приближения также должны быть мнимыми, Между численными методами, используемыми для решения одного уравнения и систем уравнений, нет принципиальных различий. Следовательно, основным параметром, определяющим точность решения, является порог, при достижении которого функция считается равной нулю. Как вы помните, при использовании функции root этому порогу соответствовала системная переменная T0L Ту же роль исполняет данная переменная и при решении систем уравнений. Уменьшая T0L, вы увеличиваете точность, однако прн этом возрастает время расчета и чувствительность к виду функции. Минимальное значение TDL - 10",7,стандартш>с - 101. Стоит воздержаться от «профилактического» назначения TDL минимального значения. Дело в том, что количество итераций, которые может совершить численный метод, ограничено ввиду накопления ошибки. Поэтому при очень малом значении 101 имеется вероятность, что алгоритм просто не доберется до корня, исчерпав лимит на количество итераций. Величина TDL должна задаваться исходя из того, сколько знаков в ответе действительно значимо. В большинстве случаев TOL-10 обеспечивает вполне Приемлемую точность. Рис, В.11. Пинии нулевого уровня дпа системы хг+у,-8п(уИ15 и Sln(x)+sin(y)30.5 При решении линейных уравнений в блоке Given-Find TOL не оказывает влияния на точность результата. В Mathcad реализовано несколько алгоритмов численного решения систем уравнений. Если алгоритм, используемый по умолчанию, не справится с задачей, можно попытаться сменить его иа другой. Для этого щелкните правой кнопкой мыши на тексте функции find. При этом откроется контекстное меню, в котором среди стандартных команд имеются три пункта, определяющие тип используемого метода. □ Пункт AutoSelect (Автоматический выбор). Численный алгоритм и его настройки будут определены автоматически. Если система линейная, то будет использован соответствующий метод. Если она нелинейная, то сначала будет осуществлена попы гка найти решения методом сопряженных градиентов. Если она окажется неудачной, то будет задействован метод Левснберга. Если И он окажется неэффективным, то система применит квази ньютоновски и метод. Чаще всего нет никакого смысла менять пункт AutoSelect на какой-то другой, гак как при его активности Mathcad самостоятельно будет пытаться найти решения всеми доступными способами. Сменить его стоит лишь, если вы хотите применить тонкие настройки или же получить решение каким-то конкретным способом. АХ?) - if\x +у tKy] -1Ъ 0.1,0} -tf(«eO(i + ео<# - 03 > 0.1,0) 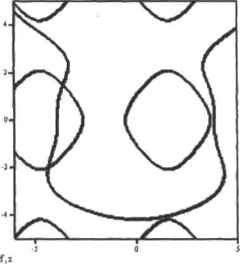 0 ... 96 97 98 99 100 101 102 ... 177 |












