Раздел: Документация
0 ... 98 99 100 101 102 103 104 ... 177 серьезно исказить результат- Так, например, при решении систем уравнений аналитической химии для определения рН какого-то вещества илн смеси веществ, искомое значение концентрации ионов водорода обычно весьма мало. Поэтому, при использовании численных методов, оно зачастую просто округляется до нуля. А так как рН — это отрицательный лесятичный логарифм от концентрации Н*, то вполне понятно, что при таком округлении его значение правильно вычислено быть не может. Если же для решения этой задачи использовать символьный процессор, то ответ будет найден без каких-либо трудностей. Это связано с тем, что символьный процессор при приблизительном решении систем алгебраических уравнении использует арифметику длинных мантисс и предельный уровень точности увеличивается до 10 к. Однако, увы, такой ПОДХОД применим только к простейшим, алгебраическим системам. В следующем примере предложено решение подобной задачи. Изучив его, вы поймете преимущество используемой символьным процессором арифметики длинных мантисс, а также важность верного выбора численнот метода. Если вы не владеете элементами химии, то просто рассмотрите решение данной системы с точки зрения трудностей, которые могут возникнуть при малой величине параметров илн корней уравнений. Пример 8,33. Определение рН миплимолярного раствора гидрофосфата натрия Начальные услония (к., - константа диссоциации гидгхчросфата. Ц — дигндрофосфата, - кон-стаыта диссоциации поди. С — концентрации пшрофосфага): к3:=4.8]0" 13 k2; = 6.2-10"8 k>Hf14 С:=10~3 ПрЯНЖвНМЯДгГЯ численного метала (г - конштрапня фосфата, у — гидрофосфа та, х - дшнд-роик-фата. о - ОН, h — Н*): z:*0 о := 0 h := 0 х := 0 у := О Peumnw системы уравнений, описывающей происходящие процессы диссоциации и гидролиза: Given x-h y-h = oh w X + у + 2 ш С х + 2у + 3z - о - 2С Отчет численногометол»,ислольаукццегося иоумолчании (неверный п рамках рассматриваемой задачи): find(x,y,z,o,h) 3.333 *10 3319x10 3.148x10 -1.832*10 0 Ответ метода Левенберга (точность в рам кал данной задач» приемлемая): fmd(x,y,z,o,h) =
Правильный выбор используемого метода ифает первостепенную роль для верного и легкого решения уравнения илн системы уравнений. Однако решаете ли вы задачу численно или используете возможности символьного процессора, очень внимательно относитесь к результату вычислений и при малейших сомнениях обязательно делайте проверку. Этот принцип проверки очень важен, поэтому мы еще не раз его повторим в этой книге. Постарайтесь ему следовать, и вы не допустите ошибку илн оплошность почти наверняка. Все употребляемые в Mathcad алгоритмы решения систем нелинейных уравнений относятся к так называемым градиентным, то есть связаны с приближением функций с помощью производных. Однако они могут отличаться целым рядом технических тонкостей (влияющих на эффективность алгоритмов): способом вычисления производной или решения возникающей иа определенном этапе системы линейных уравнений, условием принятия точки в качестве корня или приемом разрешения проблемы сингулярности якобиана. Но все алгоритмы решения систем уравнений в Mathcad можно отнести к модификациям метода Ньютона. Чтобы разобраться, в чем заключается данный метод и с чем могут быть связаны проблемы при его использовании, сначала рассмотрим простейший случай поиска корней одного уравнения с одним неизвестным, В атом случае принцип работы метода Ньютона довольно схож с уже рассмотренным ранее методом секущих и заключается в следующем: через определенную пользователем начальную точку проводится касательная к кривой функции, нуль которой нужно найти. В точке, в которой касательная пересекает ось X, вычисляется значение функции. Если оно меньше (по модулю) установленного минимума точности TQL. то данная точка определяется как корень. В противном случае через точку функции] которая соответствует полученному приближению, проводится вторая касательная, Точка ее пересечения с осью X определяется как вто-\»х: upon, ([г.кгциг 1Д.п значение l(Y) iHiiiii больше по мод\ но, чем TOL, провалится третья касательная. И так далее до тех пор, пока условие корня не будет выполнено (рис. 8.13). Рис, 8.13. Иллюстрация метода Ньютона, Достаточное приближение к корню достигается на пятой итерации Теперь, зная идею метода Ньютона, попробуем самостоятельно написать программу поиска корней нелинейных уравнений. Для этого сначала следует решить проблемы чисто технического плана: во-первых, нужно придумать, каким образом мы будем проводить касательные через точки приближений, и, во-вторых, как затем находить точки их пересечения с осью X. В общем случае условие пересечения прямой линии (каковой и является касательная) с осью X можно определить как: Из этого уравнения требуется найти х, однако чтобы это сделать, нужно знать величины констант к и Ь, Определить одну из них предельно просто: ведь, как известно, к численно равна тангенсу угла наклона прямой к оси X. В случае же касательной тангенс этот равен значению производной функции в точке касания. То есть: Зная к. можно очень легко найти и Ь. исходя из того факта, что в точке касания значения функции касательной и исследуемой функции совпадают. Та есть: 1 + 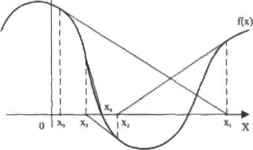 кх + Ь = О Выражаем Ь: Подставляем полученные выражения для констант в первую формулу: 0 ... 98 99 100 101 102 103 104 ... 177 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












