Раздел: Документация
0 ... 100 101 102 103 104 105 106 ... 177 в точки, в которых якобиан вырожден- А сделать это можно очень ггросто: в том случае, если такое попадание все-таки происходит, следует просто изменить рабочие значения приближений, прибавляя к ним некоторую (небольшую) величину, например T0L Рассмотрим теперь, как можно решить систему из N уравнений. В общем-то, это можно сделать точно так же, как в случае системы из двух уравнений: решая систему из N линейных уравнений, в качестве матрицы коэффициентов которой выступает якобиан, вектора неизвестных — вектор разностей новых н старых приближений, вектора правых частей — вектор значений соответствующих уравнениям функций в точке текущего приближения, взятых с противоположным знаком. Язык программирования Mathcad слишком примитивен, чтобы нз нем можно было реализовать функцию, способную решать системы из произвольного количества уравнений. Поэтому мы ограничимся созданием функции, позволяющей решать системы из двух нелинейных уравнений. sys(f,p,xO,yO,TOL): (й *- 0 х <- хО у0 *~ уО ) dFj[z,x,y)<--z(x,y) dFv(z,x,y)«--z(x,y) ЙхЭу whfle <vOI>TOLv Kvv)l>T0L return crror("Dont converge to a solutions" ) if n > 100 J4dF4)№yKi (Vl*"Xn+T0L yB+l*"yn + T0L n*~D+l continue) if IJ = 0 Isolve fx ,*-Z--x у , «— Z. - у n+-n + l Попробуем решить с помощью созданного алгоритма следующую систему уравнений: X +у =16 у = sin(x) Для данной системы довольно легко подобрать начальные приближения. Это связано с тем, что в обоих уравнениях можно выразить одну переменную через другую, по причине чего система может быть визуализирована двумя кривыми. Корням же будут соответствовать пересечения этих кривых (рис. 8.14). 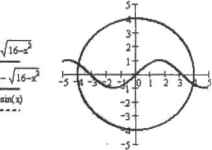 Рис. S. 14. У системы будет два решения. Первое будет расположено вблизи точки (4,-1), второе — (-4, 1) С определением корней рассматриваемой системы, ввиду того, что мы знаем приблизительное расположение решений, программа sys легко отравится: * 2 2 16- к - у sys(f,pA-I,]0 13)= ( 3.9358754812 -0.7133611965 4> Р<ЛУ) -= y-sin(x) ey-(f,p.-4,l,10 13) = f~3.9358754812) 0.7133611965 4 В основе функции find лежат куда более сложные алгоритмы, чем созданный нами. Однако базовая концепция у них та же — метод Ньютона. Поэтому мы можем легко предсказать, какие у них будут слабые места. Чтобы решение было найдено, начальные приближения должны быть близки к корням. Если между приближением и корнем окажется экстремум, разрыв или область медленного изменения функции, то численный метод, скорее всего, не сойдется. Главная сложность заключается в том, чтобы такие приближения найти. Задача эта трудная и. если в системе больше двух уравнений, практически нерешаемая. По этой причине использовать численные методы решения систем уравнений крайне сложно. Увы, но универсальных и надежных алгоритмов пока не существует. 8.2.4. Приближенное решение систем уравнений Очень часто приходится сталкиваться с системами, не имеющими решения. Однако иногда необходимо выяснить, при каких значениях переменных система не согласована наименее, иначе говоря, имеет минимальную невязку, Для решения задач такого рода в Mathcad имеется специальная функция minerr(xl„..), По особенностям своего применения она абсолютно идентична функции find, то есть также требует ввода ключевого слова Given и определения начальных приближений. При своей работе функция miner использует те же численные алгоритмы, что и функция find. Таким образом, те выводы, которые были сделаны нами в предыдущих подразделах для функции find, можно абсолютно спокойно распространить и на функцию minerr, единственным отличием принципов работы которой является другое условие прекращения итераций. Так, функция minerr возвратит последние приближения при исчерпании лимита на итерации и вычислительные ошибки вне зависимости от того, удовлетворяют ли они критериям сходимости к корню или же нет. Очень часто функция minerr оказывается способной найти те корни, которые не может определить find. Поэтому ее рекомендуется применять тогда, когда find оказывается не на высоте. Однако при этом нсюходимообязателыю осуществлять проверку найденных корней. Сравним работу функций find и minerr при решении уравнения х+у1-0. Уравнение это имеет только один корень (х-0, у-0) и является частным случаем функции, дающей поверхность в виде параболоида (рис. 8.15). Рис. 8.15. Поверхность имеет с плоскостью ХОТ лишь одну общую точку Особенностью нуля данной функции является то, что он относится по типу к касанию. Это вообще-то довольно трудная ситуация ДЛЯ любого из численных методов (особенно градиентных) и будет хорошей проверкой для обеих функций: НазтотраэАпо и minerr оказались на высоте и нашли решение верно. Но если попробовать решить аналогичное дан ному уравнение вида к-х+уМ) при большом значении к (например, 1000), то упомянутый параболоид столь исказится, что найтн корень с помощью функции find не получится ни при каком приближении, кроме х-0, у—0 (но это нельзя назвать успехом, поскольку при таких начальных точках (происходит «прямое □опадание»). А функция minerr справится с. этой задачей легко. 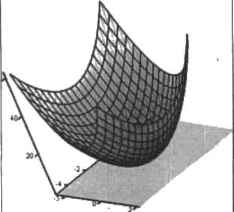 Given Given 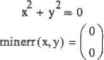 0 ... 100 101 102 103 104 105 106 ... 177 |












