Раздел: Документация
0 ... 102 103 104 105 106 107 108 ... 177 Ответе стандартной форме: хе(-°=; -3) и {2,5; 5). х< -4 х2-(2х-9)-(х- I)3 (х+4)5-(2х-6)4 х = 0 <l 0 solve ,х —> (1 5Х)-(Х< (3 <х)/х5 Ответ в стандартной форме: хб (-—; -4) и О \J I; 3) и (3; 4,5]. 2 х + х+ 1 > О solve,х -*-х Ответ в стандартной форме: хе R. Ответ а стандартной форме: в*2 или ае{-~; 2) и (2; Как вы уже, наверное, заметили, Mathcad выдает ответы в несколько отличном от принятого в нашей математике виде. Поэтому зачастую самой трудной частью работы при символьном решении неравенств является интерпретация результата. Тут нужно запомнить несколько правил. □Ответ оператор sotve возвращает в виде вектора, содержащего элементарные неравенства. Каждое такое неравенство описывает область, в которой решаемое неравенство справедливо. Если область открытая (то есть одной иа ее границ является бесконечность), то задающее се элементарное неравенство будет иметь вид х>а илн х<а. В стандартном виде такие области запишутся как те (а; «>) или .те (• »: а) Если область замкнута и ее границам соответствуют значения аргумента а и Ь, то она будет описана элементарным неравенством вида (а<х)(х<Ь). В стандартном виде эта запись будет выглядеть каклге (а.Ь). □Области в векторе ответа будут расположены строго в направлении числовой осн. По:>тому преобразовывать в стандартную форму его можно чисто механически, сохраняя исходный порядок областей. Для объединения обозначений областей в одно выражение используется символ <и». К примеру, следующий вектор элементарных неравенств В стандартной форме запишется как хе(—; 1) и (2; 3) kj (4; ™). Знак умножения, стоящий в решении между элементарными неравенствами, эквивалентен логическому «И». Mathcad же, анализируя логическое выражение, возвращает 1, если оно оказывается истинным, и 0 в случае невыполнения его условия. Так, если оба элементарных неравенства верны, решение исходного неравенства также верно: 11-1. Если же условие хотя бы одного из них не выполняется, решение неравенства будет ложным: 1 0-0,0 1-0. х< 1 (2<хИ*<3) 4 <х Q Нужно внимательно следить, используются ли в описывающем область элементарном неравенстве операторы «больше» и «меньше» («<» и *>»)илиже «больше ил и равно* и «меньше или равно» («<► и «>»). В первом случае точку границы не нужно включать в область, во втором — нужно. Если граничная точка входит в область, то в стандартной форме ее записи используется квадратная скобка, если не входит—круглая. Например, неравенство (3<х)(х<9) в стандартную форму записи решения неравенства преобразуется какхе(3;9. □Если в решение неравенства входит отдельная точка а, то Mathcad использует обозначение х-а (см. второе неравенство в примере 9.1). □Если неравенство выполняется при любых значениях аргумента, то в качестве ответа программа возвратит сам аргумент (см. третье неравенство в примере 9.1). □Если неравенство не выполняется при любых значениях аргумента, то Mathcad возвратит сообщение об ошибке: No solution was found (He было найдено решения). Однако полностью полагаться на это сообщение ни в коем случае нельзя. Вполне вероятно, что программа просто не смогла справиться с задачей. В подобных случаях обязательно необходимо проводить дополнительные исследования, например, с помощью графика. □В выдаваемых ответах оператор solve никогда не использует знак <*», Даже если неравенству не соответствует только одна точка (см, четвертое неравенство в примере 9.1), области решения описываются полностью. Однако в таких случаях все же техничнее давать ответ в форме х*а. Объективно говоря, полностью доверять символьному процессору Mathcad можно лишь при решении очень простых неравенств, выраженных алгебраическими полиномами или отношением полиномов. Во всех остальных случаях нужно быть очень внимательным и обязательно проверять решение. Так, программа сделает ошибку практически в любом неравенстве, содержащем корни (см. пример 9.2). Пример 9.2. Неверное решение неравенств Преобразуем ответ в стандартный вил: хе(-~; 2)о (9;<~), Анализируя его, обнаруживаем, что он не до конца верный. Так как в выражении проводится операция извлечения корня нзх, последний должен быть больше либо равен нулю. Следовательно, первая область решения найдена некоррект-л1 а верный ответ будет иметь вид хе(0; 2) и (9: о°). В иго правильности можно убедиться, построив График (рис, 9.1). Аналогичную описанноfl лыше ошибку сделает Mathcad и при попытке решить другое неравенство с корнем: Ответ в стандартной форме: х€ (-~3). Полученный результат неверен, так как подкоренное выражение не может бьгтъ меньше нуля. Правильный ответ — хе(-б!:3). Достаточно неплохо справляется оператор solve с показательными и логарифмическими неравенствами. Однако при их решении нужно, как и в случае неравенств с корнями, обязательно делатьПроверку по графику. Если в качестве ответа система выдаст громоздкое выражение, его следует попытаться упростить с помощью оператора simplify. 61 > х+ 5 solve,х —t х< 3 1 Ют о 10 I Рис. 9.1. Соответствующая неравенству функция отрицательна на промежутке от 2 до 9 Пример 9.3. Решение показательного неравенства Рис, в.2. Функция отрицательна, еслих> 12 Вывод: неравенство было решено верно. Компьютер лишен интеллекта. Глупо рассчитывать на то, что при решении задачи Mathcad применит хитроумный прием или незаурядный ход. Программа решает простые неравенства стандартными способами — и не больше. Поэтому очень часто пользователь должен * помогать» символьному процессору, приводя задачу к более простому виду. Как унростить неравенство? Во-первых, можно произвести замену переменных. Во-вторых, можно путем алгебраических преобразований привести выражение к более легкому для программы виду. В-третьих, можно производить логарифмнрова- Ответ и стандартном виле; хе {-12; »). Проверяем верность найденного решения с помощью графика {рис. 9.2). 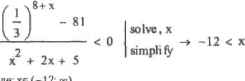 12 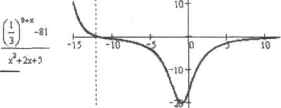 0 ... 102 103 104 105 106 107 108 ... 177 |












