Раздел: Документация
0 ... 99 100 101 102 103 104 105 ... 177 Из этого простого уравнения с одним неизвестным находим требуемую точку пересечения касательной с осью X: Данная формула носит название формулы Ньютона. Зная ее,реализовать соответствующий численный метод предельно просто; х = хп- Newton(f,a,TOL) := (" +- 0 х •*- а df(x) <- Н-ДЮ dx while I x «- x + TOL on error l + dfx n nVn/ Vl*-Xb-<Xn)+df(Xn) B4-0 + I return (xn nj if f(xfl) < TOL л )- f(x) < TOL return error("Donl converge to a solution!" ) if о > 100 В коде программы Newton есть несколько тонкостей, которые стоит прокомментировать. □Производную от f(x) необходимо задать как локальную функцию clf(x). Это связано с тем, что если использовать оператор дифференцирования в выражении, соответствующем формуле Ньютона, напрямую, то возникнет ошибка (так как система воспримет f(xip) как постоянную величину, а не функцию от х). □Если очередное приближение совпадет с экстремумом, то возникнет ошибка деления иа нуль. Обойти эту проблему просто. Для этого нужно, при возникновении ошибки, прибавить к текущему приближению небольшую величину (например, TOL). Точка нового приближения сместится в сторону от точки экстремума, и поэтому значение производной в ней уже не будет равно нулю. □Метод Ньютона является локально сходящимся. Это означает, что то, сойдется он к корню или нет, зависит от правильности выбора начального приближения, Важно предусмотреть ситуацию, в которой неудачное приближение породит расходящуюся последовательность приближений. В программе Newton отслеживается количество проделанных итераций. Если оно превышает 100, то возвращается сообщение об ошибке. Проверим, насколько эффективна программа Newton, решив уравнение, корень которого можно точно найти с использованием оператора solve: f(x) :=sta(x) - х sin(х)--solve,х 2.772604708265991234 К Newton 2.77 26 04708265 9 9n 7 Прочерка показывает, что метол Ньютона сходится очень быстро. Каждая итерация увеличивает точность в среднем на два знака мантиссы. Это больше, чем в случае таких методов, как метод секуших или Больцано. Но этот вывод вовсе не означает, что для решении всех уравнений лучше использовать вычислительный блок Given-Find (реализующий для нахождении корней одного уравнении с одним неизвестным схожий с описанным алгоритм). Все дело в том. что для метода Ньютона характерны те же недостатки, что и .тля метода секуших (трудности в поиске решений при наличии экстремумов, перешбов, точек разрыва и особенностей поведения функции на бесконечности). Однако, помимо этого, к описанным недоетатгслА{до6авля10тсяе1цен многочисленные проблемы, возникающие в связи с использованием производной. Поэтому в случае сложных уравнений лучше не рисковать и применять для решения более надежный алгоритм секущих (а еще лучше глобально сходящиеся методы интервалов локализации корня). Вообще, на практике метол Ньютона редко используется (ввиду описанных недостатков) дли решения одиночного уравнения. Однако очень важно его расширение длн систем уравнений. Конечно, в нем не исчезают присущие этому алгоритму слабости и недостатки, но лля поиска решений систем уравнений просто пока не создано ничего лучшего. Попробуем самостоятельно расширить метод Ньютона на случай систем уравнений. Для начала разберемся с наиболее простым случаем и придумаем идею алгоритма решения системы из двух нелинейных уравнений. Для этого вспомним, что любое такое уравнение — это частный случай (точка нуля) некоторой функции ?М(х, у), которую можно представить в 1фОстрз11ствекак поверхность. Очевидно, что решением системы уравнений будет являться точка на линии пересечения (или просто точка касания) поверхностей, соответствующих каждому из уравнений- С другой стороны, значения обеих функций Н такой точке должны быть равны нулю. Итак, с тем, какой геометрический смысл имеет точка корня системы из двух уравнений, мы разобрались. Но как можно найти такую точку? Чтобы ответить на этот вопрос, вспомним, как мы справились с этой проблемой в двумерном случае. Тогда удалось найти корни благодаря тому, что сложндас кривые были заменены на простую и техничную прямую. Перв;1Я мысль, которая возникает» ~ 3Ttl просто повторить этот проверенный н такой эффективный шаг. Однако проблема заключается в том, что поверхность нельзя аппроксимировать прямой! Это то же самое, что заменить Кривую точкой; глупо и бессмысленно. Поверхность должна быть заменена каким-то, по возможности более простым и легко нсследуемыМ, но объемным объектом. Очевидно, что таким объектом является плоскость. Не менее очевидно, что две плоскости, приближающие в данной окрестности некоторые поверхности, почти наверняка пересекутся. Результатом нх пересечения будет прямая. Л. точка, в которой дан нам прямая не ресс чет плоскость X0Y, н будет либо корнем (в лучшем случае), либо приближением. Нарисовать ими тем более представить работу алгоритма, который бы реалиэовы-вал описанную выше идею, очень сложно. Поэтому просто поверим собственной интуиции. Первый вопрос на который мы должны ответить, это как можно провести касательную плоскость к поверхности в некоторой точке. Сделать это очень ггросто: для этого записываем разложение соответствующей функции в ряд Тейлора по двум первым членам. Математической тонкостью этого действия в случае функции двух переменных является то, что разложение должно быть проведено по обеим переменным. Аналогичное выражение можно записать и для второго уравнения системы: р<х,у>=p(*Q,yn)+ piV„Xx- "О*ip(vvKy уп) Так как значение обеих функций в точке корня равно 0, то имеем следующую систему линейных уравнений: -f(vO-!(vvK*-\У~Ь - >») Из этой системы нам нужно найти значения хну, которые являются координатами точки следующего приближения (или корня). Однако, раскрывая скобки, мы лишь усложним вид системы. Поэтому на данном этапе сделаем замены: Y=y-yn X = х - хп Произведя замену, перепишем полученную систему из двух линейных уравнений в матричном виде: 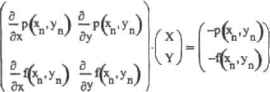 Левая матрица в произведении - это так называемый якобиан. В данном случае он играет роль матрицы коэффициентов. Решить систему можно или через обратную матрицу, или (техничнее) используя функцию Isolve. Когда корни системы будут найдены, выражаем из них координаты точки нового приближения. Если это приближение удовлетворит критериям нуля функций f(x,y) и р(х,у), то возвращаем его как решение. В противнем случае переходим к следующей итерации, Важно учесть то, что якобиан может быть вырожден. Это означает, что в выбранной точке частные производные двух функций равны, а следовательно, аппроксимирующие плоскости будут параллельны и никакой точки приближения получено не будет. Также возможна ситуация, что одна из плоскостей будет параллельна плоскости X0Y. В атом случае одна из строк якобиана будет нулевой, и он не будет нести необходимой информации, Какже таких проблем избежать? Наиболее ггростой вариант - не попадать 0 ... 99 100 101 102 103 104 105 ... 177 |












