Раздел: Документация
0 ... 101 102 103 104 105 106 107 ... 177 Однако решение уравнений с двумя неизвестными - это не главная задача функции minerr. Куда более важной с практической точки зрения является возможность ее применения для поиска точки минимальной невязки несовместной системы. Практически важный случай таких систем связан с решением задач регрессии по методу наименьших квадратов. Пример 8.34. Определение параметров нелинейной зависимости методом наименьших квадратов Существует система, совершающая затухающие колебания. Нужно определить, каким законом можно описать данную систему, если известно общее уравнение затухающих колебаний. Оно имеет вид: Y = Asin(k-t)-e b Итак, необходимо узнать, чему равны параметры A. k, t. Для этого воспользуемся следующими экспериментальными данными: 1:= (О 123456780 Ю)Т у :=(0 4381 1.084 -2.336 -1.252 1.023 1.298 -0.537 -0.954 0.024 0.749)Т Задаем функцию четырех переменных на основании общей формулы затухающих колебаний: Yrt,A,k,bl := Asin(ki)e~ b-t Задаем функцию метода наименьших квадратов. Она определяется как сумма квадратов отклонений экспериментальных данных от истинных значений зависимостн при данных величинах аргумента. last(t) Y ee(i.A.k,b):. £ (Y(t..A,k,b)~yjf i = 0 Если экспериментальные данные были получены без погрешности, то правильный подбор параметров A, k, b приведет к тому, что функция V етт будет равна 0. Если же погрешность имеется, то Y err при этом минимизируется. В первом случае параметры могут быть определены как с помощью функции find, так и Minerr, Во втором случае можно использовать только Minerr, Так как в наших данных есть довольно заметная погрешность, применяем Minerr. А:=4k:=lЬ:«о!з Given Y cn(l.A.k,b) = 0
Строим график, чтобы убедиться, что экспериментальные данные хорошо ложатся на кривую, параметры которой были найдены функцией Мшегт (рис. 8.16). 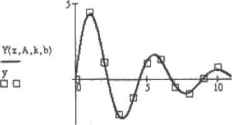 1,1 Рис. в.10. Регрессивная кривая и экспериментальные точки В Mathcad 12 появилась новая системная переменная ERR. Данная переменная хранит сумму квадратов ошибок решений, найденных Minen. По значению .тайной переменной можно сулить, насколько приблизительно были найдены корни. Если корни были определены точно, то ERR равна 0. Глава 9. Решение неравенств Неравенства — это, пожалуй, самая сложная тема школьной программы по математике. Научиться хорошо их решать очень и очень непросто, Доопределенной степени решение неравенств схоже с поиском корней уравнений. Однако в случае неравенств дело осложняется тем, что, но сути, необходимо исследовать поведение функции на всей числовой оси, что требует очень хорошего знания математических приемов н развитой логики. Система Mathcad способна помочь в непростом деле решения неравенств. Однако ни в косм случае нельзя полагаться на программу целиком. Неравенства — это слишком тонкий предмет, чтобы можно было требовать многого от линейно мыслящей машины. Решая неравенства. Mathcad нередко ошибается или просто не справляется с задачей. Поэтому, получив ответ, era обязательно нужно проверить по [•рафику. Если же программа окажется в тунике, следует попытаться ей помочь, вручную преобразовав неравенство в более простую форму, Сложные неравенства обычно оказываются Mathcad «не по зубам». В таких случаях вы должны вспомнить, чему вас учили на занятиях, и попытаться решит!, задачу самостоятельно. Mathcad же может вам при этом помочь, выполняя такие рутинные операции, как упрощение выражений, решение промежуточных уравнений пли построение графика. В этой небольшой главе мы попытаемся на примерах разобраться, на что же реально способен Mathcad в области решения неравенств. Для аналитического решения неравенств в Mathcad используется тот же самый оператор панели Symbolic (Символьные), что и для решения уравнений и систем уравнений. - solve. Неравенство прописывается в его правом маркере, переменная, относительна которой оно должно быть решено, — в левом. Операторы сравнения можно ввести как с клавиатуры (знаки «<» и «>► можно задать напрямую, знак «>» — сочетанием Ctrl+0, знак «5» сочетанием СсЛ>9),так и с помощью панели Boolean (Булевы). Приведем примеры решения нескольких неравенств, выраженных простыми алгебраическими выражениями. С такими неравенствами Mathcad справляется эффективнее всего. Пример 0.1. Решение неравенств, выраженных полиномами и отношениями полиномов х<-3 2х-5 > 0 solve ,х -> (х<5) 0 ... 101 102 103 104 105 106 107 ... 177 |












