Раздел: Документация
0 ... 104 105 106 107 108 109 110 ... 177 Полученное выражение содержит как синусы, так и косинусы. Чтобы в дальнейшем можно было его рассматривать как алгебраическое, нужно оставить в нем лишь один вид функций. Очевидно, что проще избавиться от косинусов. Выразив косинус через синус из основного тригонометрического равенства. Подставляем полученное выражение в неравенство (оператор substitute), а затем упрощаем его. 2sin(x)2-2-sm(x)+4-sin{x)-cos(xf substitute, cos( хГ= I - si ш x f •-Ф51П(Х)"+281П(Х]2+281П(Х) colLect,sin(x) Далее нужно, решив полученное неравенство относительно si;t{\). определить, прн каких значениях синуса оно выполняется. 32 lsin(x) + 2sin(x) + 2sin(x) - I < 0 solve,sin(x) I —-22 <sin(x) sin(x) < - I 2WA W 2) 1 -2 <sm(x) 2 Итак, решаемое неравенство справедливо, если sin(x)€( -Tni2\ 1/2) \j (2v3/2; t). Чтобы найти, каким должен быть х, чтобы это условие соблюдалось, проанализируем график синуса на промежутке одного периода (рис. 9.5). 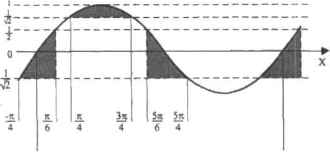 2-4-NJ-*-(N+1) Рис. 9.5. Функция y(xV=sin(x) на промежутке, равном одному периоду Отметив на оси Y границы областей решение, проведем вспомогательные линии. Заключенные между ними фрагменты кривой содержат точки, удовлетворяющие неравенству. Таких фрагментов на промежутке периода три Глядя на полученную схему, совсем не сложно найти координаты их границ по X и записать окончательный ответ х«(-х, 4 * 2-пчЧк/в + 2nN)u(n/4 + 2"Jt>N; 3*/4 + 2*N) и(5.*/64 2-*>N;5«/4 * 2-n-N),Ne Z. Глава 10, Вычисление интегралов В этой главе рассматриваются особенности проведения такай важнейшей математической операции, как интегрирование. Наряду с производной, интеграл является одним из основных инструментов современной математики. На практике очень часто ставится задача найти функцию или ее значение в точке, если известна ее производная. К подобной задаче сводятся многие физические и химические проблемы. Например, получив из эксперимента уравнение скорости химической реакции, можно с легкостью определить, сколько вешества прореагирует за определенный промежуток времени. Если тело можно описать функцией, то интегрирование позволит найти его объем и площадь поверхности. Подобных примеров можно привести очень и очень много. Аналогично дифференцированию, интегрирование в Mathcad может быть как численным, так и символьным. При символьном интегрировании система ищет первообразную, причисленном - приближенно подсчитывает ограниченную кривой функции площадь. Вычисление определенного интеграла может быть как символьным, так и численным, неопределенного - Только символьным. В случае интегрирования численный подход имеет куда большее значение, чем в случае дифференцирования. Иа это есть две причины. Во-первых, далеко не все функции имеют первообразную, которую можно вы-разнть в элементарных функциях. Во-вторых, определение первообразной - это куда более сложная задача, чем нахождение производной, поэтому Mathcad с ней не всегда справляется. Конечно, аналитический ответ куда информативнее и не содержит погрешности — поэтому сначала всегда нужно стремиться провести интегрирование символьно. И лишь в случае неудачи (или если ответ будет уж очень громоздок) следует обращаться к численным методам. Помимо обычных интегралов, в Mathcad можно подсчитывать двойные и тройные интегралы, а также несобственные интегралы. В подсчете таких интегралов есть важные особенности, поэтому им мы посвятим отдельные подразделы. 10.1. Нахождение неопределенного интеграла Панель Calculus (Вычисления) содержит два оператора интегрирования. Первый, Indefinite Integral (Неопределенный интеграл), позволяет определить вид первообразной интегрируемой функции (рис. 10.1). Помимо панели, ввалится данный оператор сочетанием Ctrl+I. TV £ 00 S тт <и I Idl amtegral Ctrl+l Рио. 10.1. Оператор неопределенного интеграле Оператор неопределенного интеграла содержит два маркера, которые заполняются полностью в соответствии с принятыми в математике традициями; в левый вводится функция (или имя функции), под знак дифференциала — переменная, по которой должно быть проведено интегрирование. Использовать с оператором неопределенного интеграла можно только оператор символьного вывода <», Пример 10.1. Вычисление первообразных Интегрирование сложной рациональной функции: 10х + Вх + 16 я2 - lSi-21 dx-» 1Г>х + 79-lnVx- 15-х 309 atanb Интегрирование функции с иррациональностью: — dx factor -» —2 2 х + 1 L V*f J Интегрирование Тригонометрической функции СНеоиределениыми коэффициентами ( Ulan х- 1 + и —-{2-а- 15)309 309 1 1 Х + 2 х +1 - ta x-cos(x)2dx simplify 1 / \ a2-cos{2-x) + 2-sin(2x)-a + + 4 -expCa.x)--( 2 \- Зачастую результат интегрирования тфедегавляет собой громоздкое выражение. В этом случае его стоит упрощать. Наиболее универсальный инструмент, который для этого используется, — это, конечно, оператор Simplify (Упростить). Однако иногда выражение можно сделать проще, приведя подобные слагаемые (оператор Collect), разложив степени (оператор Expand) или приведя дроби к общему знаменателю (оператор Factor). Чтобы задействовать нужный символьный оператор, следует выделить выражение интеграла и нажать соответствующую кнопку на панели Symbolic (Символьные). Применять к Х!эулътату интегрирования можно и сразу несколько симаолыгьгх операторов. Строго говоря, неопределенный интеграл — это множество всех первообразных функции. Неопределенный интеграл отличается от выражения первообразной наличием произвольной постоянной (обычно она обозначается буквой С). Однако в выражения, возвращаемые оператором неопределенного интефирования Mathcad, произвольная постоянная не входит, так как в случае большинства практических задач С — это довольно бесполезный балласт. Однако порой произвольную постоянную нужно учиты- 0 ... 104 105 106 107 108 109 110 ... 177
|
