Раздел: Документация

0 ... 24 25 26 27 28 29 30 ... 87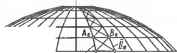

й г, h с* в*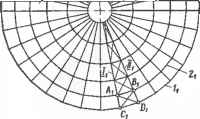

Черт. 6.3.1. Сетчатая несущая конструкция купола (геометрическая схема).

Разрез Д-Д

X

J- Ш J. 642 у

Треугольный элемент (грань тромиВы}

Г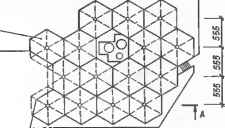

83

Черт. 6.3.2. Многогранная поверхность покрытия

Черт. 6.3.4. Железобетонные тонкостенные пространственные конструкции покрытий: а...в — складки соответственно трапециевидная, треугольная и сложная; ;вездчатый купол.

Черт. 6.3.3. Использовние-оверх- покрытия. Фрагмент интерьера ноет и пирамиды &ля образования столовой.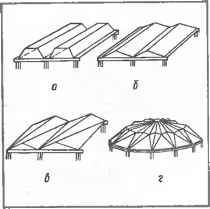

§ 6.4.

СПОСОБЫ ЗАДАНИЯ

И КОМПЛЕКСНЫЙ ЧЕРТЕЖ

КРИВОЙ ПОВЕРХНОСТИ

6.4.1. Кривой поверхностью называют непрерывное множество последовательных положений образующей линии, движущейся в пространстве. На черт. 6.4.1 показаны образующая /. ее последовательные положения Iх... Г при движении по направляющей m и образованная при этом поверхность Ф.

В общем случае одна направляющая линия m не определяет однозначно движение образующей i. Поэтому используют также две или три направляющие, в качестве которых могут быть кривые и прямые линии, плоскость, поверхность, точка. Такой способ образования кривой поверхности называют кинематическим; он позволяет задать поверхность непрерывно, так как при известном (или заданном) законе пер: ml ...ни обеспечивает возможностг построения любого положения образующей и любой точки поверхности из

непрерывного множества этих элементов.

По виду образующей / кривые поверхности делят на прямо линейчатые {/—прямая) и криволинейча-тые (/ — кривая постоянного или переменного вида).

Черт. 6-4.1. Кинематический способ образования поверхности.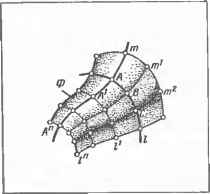

По развертыванию поверхности делят на развертывающиеся, обладающие свойством точного развертывания в плоскость (конКЦеСие. цилиндрические и поверхности с ребром 5С2?ра-та) и неразвертывающиеся. 6.4.2. Способы задания: аналитически в общем виде уравнением F(x, у, г} = 0. Для изображения на чертеже такое задание мало пригодно, так как задается бесконечное количество точек и не обеспечивается наглядность; точечным каркасом поверхности. При этом на чертеже задается конечное количество точек поверхности, удовлетворяющих определенные условия. Задание дискретно (прерывно). Самой поверхности принадлежат только точки Л, В, С, А", ... каркаса (см. черт. 6.4.1), промежуточные точки строят приближенно. Применяется в геодезии, топографии .для задания рельефа поверхности земли;

линейным каркасом поверхности. При перемещении линии каждая ее точка А, В, С, ... опишет в пространстве некоторую линию т, т1, пг2 ... (см.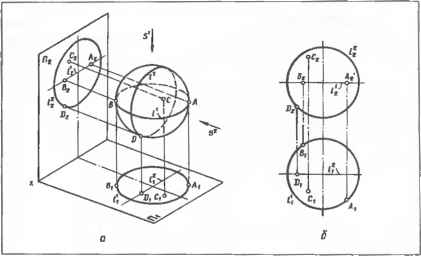

---

Часть вторая.

черт. 6.4.1). Таким образом, вся поверхность Ф окажется покрытой сеткой линий /, / и т, т\ т2 .... которая является линейным каркасом поверхности. Чертеж каркаса точнее и нагляднее отображает поверхность, так как все линии принадлежат поверхности. Применяется в геодезии, топографии и картографии, в чертежах вертикальной планировки и земляных работ, при проектировании и изображении кривых поверхностей покрытий зданий и т. п.; определителем поверхности, т. е. совокупностью направляющих и образующей линий поверхности с указанием закона ее перемещения. Элементы, входящие в определитель, называют параметрами определителя. 6.4.3. Кривую поверхность на чертеже

псадкеГ опрелелителем в ™едУюц*емЧерт. 6.43. Сфера:Черт 6.4.5. Цилиндрическая по-

формулируют определение поверхнос-верхность:

ти;а — проецирование; б — комплексный а — образование; б — прототип; в —

на основе определения составляют оп-чертеж.задание на комплексном чертеже,

ределитель поверхности. Определитель

Черт. 6.4.2. Проецирование поверхности.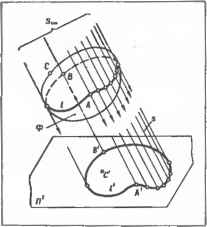

Черт. 6.4.4. Наклонный эллиптический цилиндр. Пример дополнения очерков проекций изображениями пх\ и mo> Si и S2, li и /2 параметров определителя поверхности.

J It/
i	г )

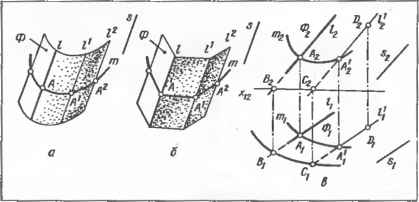записывают в скобках после обозначения поверхности, например, «D[mX(/s)], где m — направляющая линия; / — образующая прямая; s — неподвижная прямая; при движении образующая I сохраняет параллельность прямой s и пересекает направляющую т; вычерчивают проекции параметров определителя и указывают закон перемещения образующей *. Такой комплексный чертеж поверхности является полным и представляет собой плоскостную модель, геометрически равноценную поверхности-оригиналу. 6.4.4. Для обеспечения наглядности чертежа поверхности изображают проекциями контуров видимости ее, т. е. линиями очерков проекций. Часто контуры видимости полностью или частично совпадают с краевыми линиями, ограничивающими поверхность. Параллельные проецирующие лучи s, касающиеся поверхности Ф, образуют проецирующую цилиндрическую поверхность (черт. 6.4.2). Линию касания проецирующей поверхности с поверхностью Ф называют контуром видимости /. Линию пересечения проецирующей поверхности с плоскостью проекций [[ называют очерком проекции /. Она является проекцией поверхности Ф. Точки А и В контура види-

* Использование определителя позволяет минимальным количеством элементов поверхности изобразить ее на чертеже непрерывно.

мости / спроецированы в точки А и В очерка проекции /. Любая точка С поверхности Ф, как лежащая внутри проецирующей поверхности, спроецируется в точку С, лежащую внутри очерка проекции

Для каждого направления проецирования (т. е. для каждого положения STO центра проекций) будет своя проецирующая поверхность, свой контур видимости и свой очерк проекции одной и той же поверхности Ф На черт. 6.4.3, а представлена сфера (замкнутая поверхность) и ее проекции. Очерком горизонтальной проекции сферы будет окружность 1\, являющаяся проекцией окружности — линии / контура видимости относительно плоскости проекций [(sJ-fli). Очерком фронтальной проекции сферы является окружность 1\ — проекция окружности — контура видимости /2 относительно

IKs2J-[b)-

Окружность / , не являясь контуром видимости относительно плоскости проекций Пг. проецируется на нее в линию /г, расположенную внутри очерка проекции / поверхности. Точки А, В, лежащие на контуре видимости / относительно плоскости проекций [] (черт. 6.4.3, б), проецируются в точки А\, В, линии очерка проекции /! поверхности на этой плоскости. Все другие точки С поверхности проецируются в точки, лежащие внутри очерка проекции.

---

Глава 7. Разрезы, сечения и развертки поверхностей

Черт, атр.

6.4.6. Двухзальный киноте-

6.4.5. Во всех случаях на изображении должны быть выделены параметры определителя или изображение дополнено этими параметрами (черт. 6.4.4). Таким образом достигается сочетание наглядности изображения с геометрической определенностью его, что обеспечивает непрерывность задания и правильность построения чертежа поверхности, ее граничных линий, линий пересечения с другими поверхностями, построение

разверток и, в конечном итоге,— правильное отображение архитектурного замысла. В некоторых случаях невозможно построить очерк проекции без задания параметров определителя поверхности.

Задание поверхности проекциями параметров ее определителя в сочетании с очерками проекции является основным в архитектурно-строительном проектировании и на строительных чертежах.

6.4.6. Для примера рассмотрим задание цилиндрической поверхности на комплексном чертеже (см. п. 6.4.3).

Цилиндрической поверхностью Ф называют поверхность, образованную параллельно прямой направляющей s перемещением прямой образующей / по направляющей кривой m (черт. 6.4.5, а). При перемещении прямой / параллельно $ по направляющей ломаной т, состоящей из прямолинейных звеньев (черт. 6.4.5, б), образуется многогранная поверхность, называемая призматической. Эта поверхность является прототипом цилиндрической.

Определитель поверхности: Ф[т®(/5)]. На комплексном чертеже цилиндрическую поверхность задают проекциями параметров ее определителя, т. е- проекциями направляющей m(mi, /пг) и образующей 1(1\, /2) или направления s(si, S2) (черт. 6.4.5, в). Так как образующая, перемещаясь по направляющей, пересекается с ней, то для построения проекций случайной образующей ( достаточно на направляющей m задать случайную точку >4(y4j, А\) и провести через нее искомую образующуюl2\\s2). Чтобы построить точку D(D\, D2), лежащую на цилиндрической поверхности, необходимо провести образующую этой поверхности и задать на ней точку.

Чтобы построить основание цилиндрической поверхности, достаточно построить точки А,. С,, ... пересечения образующих /, /, ... с горизонтальной плоскостью проекций и соединить их плавной кривой линией. Пример применения цилиндрической поверхности приведен на черт. 6.4.6.

ГЛАВА 7.

РАЗРЕЗЫ, СЕЧЕНИЯ И РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

§ 7.1.

РАЗРЕЗЫ

7.1.1. Для того, чтобы на чертеже наиболее полно представить внутренние невидимые очертания предмета, применяют мысленное сечение его одной или не-

сколькими секущими плоскостями (черт. 7.1.1). Часть предмета, оказавшуюся между наблюдателем и секущей плоскостью, мысленно удаляют. Если при этом изображают только фигуру, получающуюся непосредственно в секущей плоскос-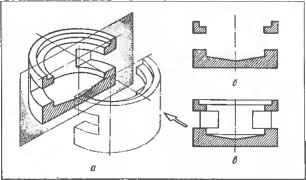

ти, то такое изображение называют сечением. Если изображают сечение и полностью или частично часть предмета, оставшуюся за секущей плоскостью, изображение называют разрезом. Мысленное сечение предмета, относится только к данному сечению и лет разрезу и не влечет за собой изменения других изображений того же предмета.

7.1.2. Правила выполнения сечений и разрезов установлены ЕСКД! ГОСТ 2.305—68**. Эти правила применяют с учетом требований СПДС, ГОСТ 21.

Черт. 7.1.1. Сечение и разрез предмета: а — схема образования сечения- б — сечение; в -разрез.

101—79 и ГОСТ 21.105— 79.

7-1.3. В зависимости от положения секущей плоскости по отношению к плоскостям проекций разрезы могут быть:

горизонтальные (планы) — секущая плоскость параллельна горизонт аль-ной плоскости проекций; вертикальные — секущая плоскость перпендикулярна к горизонтальной плоскости проекций. К ним относят фронтальные и профильные (черт. 7.1.2, с), полученные секущей плоскостью, параллельной соответственно фронтальной плоскости проекций; наклонные — секущая плоскость расположена наклонно к горизонтальной плоскости проекций. Разрез, выполненный одной секущей плоскостью, назы-

0 ... 24 25 26 27 28 29 30 ... 87