Раздел: Документация
0 ... 27 28 29 30 31 32 33 ... 87 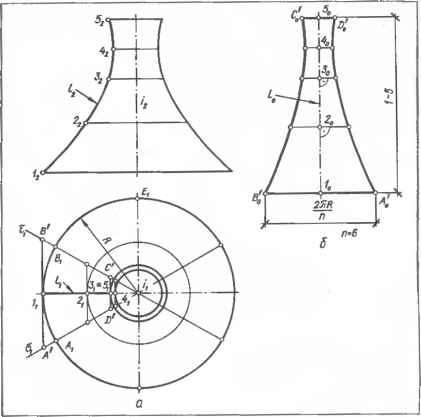 Черт. 7.3.10. Приближенная развертка не развертывающейся поверхности вращения: а — исходный чертеж; б — развертка части поверхности. Л0о0о/О, используя длину хорды с = = 10,—1,\ и длину диагонали \1N\. Затем, используя диагональ [/о0о1 как смежную сторону, строят смежный А/о0о/£ и т. д. Полученные точки 0О. h> 20, ... и 02© ... соединяют плавной кривой линией. Плоская фигура 0о°о°о0с является половиной искомой развертки. Вторая половина симметрична построенной и на чертеже не изображена. 7.3.13. Развертка боковой поверхности прямого кругового конуса представляет собой сектор круга радиуса, равного длине образующей этого конуса /= /?2-f-ft2 . Центральный угол а сектора вычисляют по формуле а= 360°/? =—-— (черт. 7.3.7, а, б). Для повышения точности построения развертки центральный угол а сектора строят как угол при вершине равнобедренного треугольника с основанием с=21 sin ~ (хорда дуги сектора) и боковыми сторонами, равными I (черт. 7.3.7, б). Построение развертки Af)fir,BvAv боковой поверхности усеченного прямого кругового конуса ясно из черт. 7.3.7, в. При недоступной вершине S конуса и. следовательно, при недоступном центре S0 сектора для построения развертки боковой поверхности усеченного конуса вычисляют длины образующих / и /, угол а и длины хорд верхней и нижней дуг с—21 sin ~ и с1 =2/sin - . За- тем строят равнобедренную трапецию А0В0В0А0 высотой =(/—/) cos а/2 (см. черт. 7.3.7, в). От середин оснований С и D по оси симметрии откладывают длины стрел / и У, вычисляемые по формулам / = —cos и fl = ll (/— cos и получают точки С0 и D0, принадлежащие искомым дугам секторов. Через три точки А0С0А0 и B0DCBC проводят дуги концентрических окружностей. 7.3.14. Примером составных поверхностей являются поверхности диффузоров (черт. 7.3.8), применяемых при соединении труб различных диаметров и формы поперечных сечений например, в вентиляционных системах, при устройстве бункеров и т. п. Обычно форма переходного диффузора состоит из участков поверхностей эллиптических конусов, сопряженных плоскими фигурами, касательными к двум ближайшим коническим участкам. Развертка диффузора состоит из разверток поверхностей конических участков с промежуточными треугольными вставками. На черт. 7.3.9, а изображена развертка составной поверхности косого диффузора для перехода от квадратного сечения к круглому с одновременным смещением осей. Форма поверхности диффузора составлена из четырех конических попарно равных участков I) и IV, сопрягаемых четырьмя плоскими участками — треугольниками I, III, V, причем два треугольника III равны. Каждый конический участок разбит на шесть делений, что соответствует делению окружности основания на л = 24. Половина развертки поверхности диф- ная с точки О, пересечения ее с плоскостью симметрии о (ai), делящей поверхность и, следовательно, ее развертку на две симметричные части. Через полученные точки деления 0„ /,, 2, ... и вершину S, проводят проекции образующих конуса — прямые S0„ Si/,, S,2,, ... являющиеся боковыми ребрами вписанной пирамиды. Основанием пирамиды будет правильный двенадцатиугольник 0,/,2,.../, стороны которого— хорды 0,/,, 1,2,, 2,3,..., соединяющие точки деления. Эти хорды являются ребрами при основании пирамиды и проецируются в натуральную величину с= \10,1 = 10,/,! = /,2, = .. Натуральную величину S202I» IS2/JI, 52221, ... боковых ребер определяют вращением вокруг оси J-L-П-Проводят ось симметрии развертки и от точки S0 откладывают отрезок SO0O = = S202 (см. черт. 7.3.5). Из S0 радиусом S2/2 проводят дугу и из 0О радиусом с=\0,1,\ делают на ней засечку. Точка /0 — искомая точка развертки. Затем из S0 радиусом S22a и из /0 радиусом с проводят засечки и отмечают точку 20 их пересечения и т. д Треугольники SO0O/D, S0/C2C являются совмещенными с плоскостью чертежа смежными гранями S0/, S12. ... вписанной пирамиды, а вся фигура So6"ooo — разверткой боковой поверх-ности этой пирамиды. Чтобы получить развертку боковой поверхности конуса, точки 0О, /0, 20,... соединяют плавной лекальной кривой линией. 7.3.11.Линию D0...A0B0C0...D0 сечения поверхности конуса случайной плоскостью т (см. черт. 7.3.5) строят на развертке следующим образом. Проводят секущую плоскость, например, проецирующую г (т2) I I Ji, отмечают проекции А7, В2, С2, ... точек пересечения образующих с этой плоскостью и определяют натуральный размер отрезков SA, SB, SC, ... В нашем примере использовано вращение и найденные натуральные величины S202, S2/, ... образующих. Искомые отрезки SsAl>, S2B2. S2C2 откладывают от S0 на соответствующих линиях развертки и полученные точки А0, В0, С0, ... соединяют плавной лекальной кривой линией Полученная фигура 6o...0D...6l,, D0... ...A0...D0, 60 является разверткой боковой поверхности усеченного конуса. 7.3.12.Развертку боковой поверхности усеченного наклонного конуса с параллельными круговыми основаниями и с недоступной вершиной S (вершина расположена за пределами чертежа) строят приближенно как развертку нераз-вертывающейся поверхности. Для этого оба основания разбивают на равное число п делений, например 12 (черт. 7.3.6), проводят образующие /—/ , 2—2\ 3—З1, ... усеченного конуса, полученные трапеции 111212, 22х3х3, ... принимают за грани усеченной пирамиды и проводят их диагонали /—2,21—3,... Определяют натуральный размер длины образующих и диагоналей по способу прямоугольного треугольника. Длину хорд с и с1 измеряют по горизонтальной проекции: с=\0,—/,1 = /—2,\ = = ...; с1=\0\-1\\ = \1\-2\\ = ... Для построения развертки проводят ось симметрии и откладывают на ней натуральный размер 0О0 = 0W образующей [00] (см. черт. 7.3.6). На 0О0£), как на стороне, строят 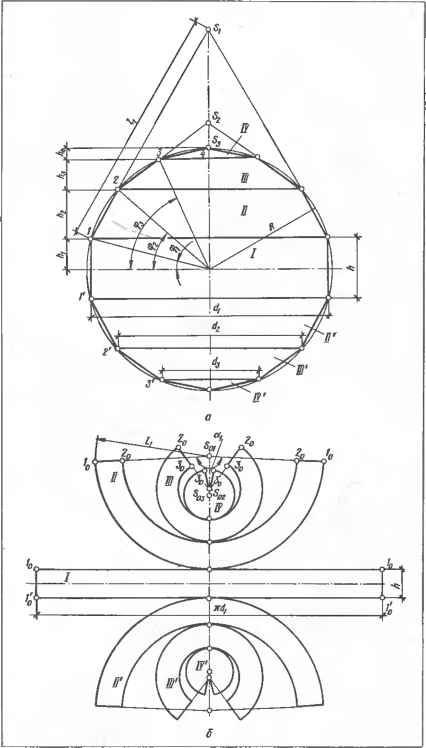 Черт. 7.3.11. Построение развертки сферы: а—аппроксимация сферы; б приближенная развертка. фузора изображена на черт. 7.3.9, б, вторая половина симметрична. Чертеж развертки выполнен с учетом размеров фланцев. Припуски 15 мм по всему контуру учитывают образование сварных швов внахлестку и присоединение к фланцам. Построение развертки выполнено по способу треугольников (см. п. 7.3.10). 7.3.15. Способ вспомогательных описанных цилиндрических поверхностей применяют для построения приближенных разверток неразвертывающихся поверхностей вращения. Способ состоит в том, что поверхность вращения меридианами разбивают на равные части, каждую часть аппроксимируют описанной цилиндрической поверхностью, которую и развертывают. Рассмотрим построение приближенной развертки поверхности однополого гиперболоида (черт. 7.3.10, а). Горизонтальную проекцию основания разбивают на произвольное число л равных частей \AtB\\=\BiEi\=.... В рассматриваемом примере л = 6. Точки А\, В{ деления располагают симметрично точке /, горизонтальной проекции /( главного меридиана. Через полученные точ- 7.3.16. Способ вспомогательных вписанных (или описанных) конических и цилиндрических поверхностей применяют для построения приближенных разверток неразвертывающихся поверхностей вращения. Способ состоит в том, что поверхность разбивают параллелями на пояса. Пояс поверхности заменяют вписанным (или описанным) усеченным прямым круговым конусом, основаниями которого являются параллели, ограничивающие этот пояс. При равенстве радиусов таких параллелей пояс поверхности заменяют прямым круговым цилиндром радиуса, равного радиусу этих параллелей. Затем строят развертки повеохностей аппроксимирующих конусов (см. п. 7.3.13) и цилиндров (см. п. 7.3.6). Эти развертки в совокупности составляют приближенную развертку поверхности вращения. Применение способа показано на примере построения приближенной развертки сферы. Поверхность сферы (черт. 7.3.11, а) параллелями /, 2, 3 и /, 2, 3 разбивают на сферические пояса /, , III, II, III и сферические купола IV, IV и заменяют: пояс / прямым круговым цилиндром; пояса ИП и 111 = 111 — усеченными прямыми круговыми конусами и купола IV = IV — прямыми круговыми конусами. ки деления А\, В\, Е\ ... и центр i\ проводят меридиональные плоскости o(oi), т(т)..., пересекающие поверхность по меридианам и делящие ее на равные части (доли). Затем фронтальную проекцию h главного меридиана делят на дуги /2—22, 22—32, минимально отличающиеся по длине от их хорд и через полученные точки 22 и 2„ 32 и 3, ... проводят проекции параллелей данной поверхности. Часть A BCD поверхности вращения, заключенную между смежными меридианами AD и ВС, заменяют касательной по главному меридиану I вспомогательной описанной цилиндрической поверхностью ABCD, ограниченной плоскостями сит этих меридианов, и развертывают эту часть цилиндрической поверхности. Для построения развертки части ABCD цилиндрической поверхности (черт. 7.3.10, б) на произвольной вертикальной прямой от случайной точки /с последовательно откладывают отрезки 1()20= I /222, 2030 = 22321, и получают спрямленный главный меридиан /0— 50=/—5. Через полученные точки /0, 20, ... 50 проводят прямые, перпендикулярные к 10, и откладывают на них соответственно длины касательных \AB\,...\CD\. Например, от точек 10 откладывают 11СА0, = , 10В0. = ; /tA\ и т. д. Полученные точки A0...D0 и В... С0 соединяют лекальными кривыми. Плоскую фигуру ABCD принимают за приближенную развертку части поверхности вращения. Число фигур, составляющих развертку, л = 6. При построении развертки можно вместо длин касательных откладывать длины дуг. Например, вместо касательной АВ\ можно отложить длину дуги AjBj =-и т. д. ЧЕРТЕЖИ В АКСОНОМЕТРИИ 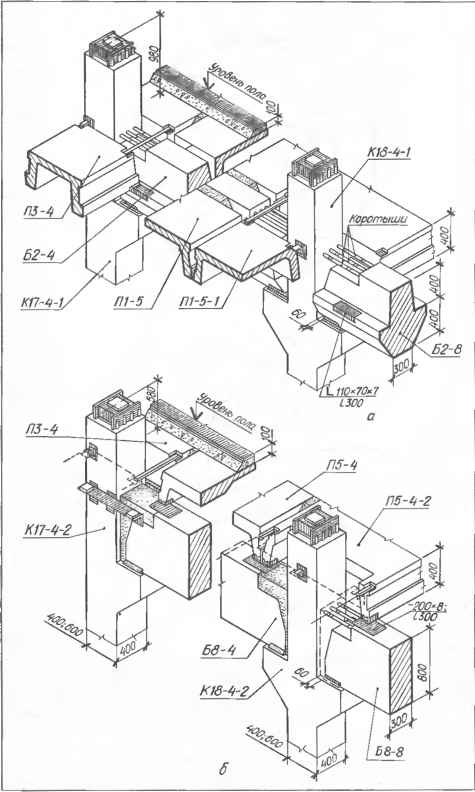 § 8.1. ОСНОВНЫЕ ПОНЯТИЯ И типы АКСОНОМЕТРИИ 8.1.1. Принятые обозначения: плоскость аксонометрических проекций — []; ак сонометрические проекции точек, линий и плоскостей — те же буквы, что и в оригинале, но с добавлением знака «штрих», например, А, а, а; вторичные проекции — как и аксонометрические, но с добавлением подстрочного индекса той плоскости, на которой находятся первичные, например, А\ Аг, А3, а\, as, Оз, af, cci. а-з; аксонометричные оси х, у, z, начало координат — О; показатели искажения по осям х, у, z, соответственно — и, v, w, приведенные показатели искажения - U, V, W (черт 8.1.1). 8-1.2. Аксонометрической проекцией или аксонометрией называют параллельную проекцию на одну плоскость фи- Чсрт. 8.1.1. Оси и показатели искажения аксонометрической системы
Черт. 8.1.2. Конструкции узлов перекрытий: а — тип 1; б — тип 2; К17 — колонна крайнего ряда; К18 — то же, среднего; Б2—ригели с боковыми полками, Б8 — то же, прямоугольного сечения; П — панели перекрытий ребристые. Черт. 8.1.3. Здание широкоформатного кинотеатра с полным железобетонным рамным каркасом. 1- бетонная подготовка; 2— монолитный железобетонный столбчатый фундамент; 3 — подпольные каналы; 4 — пол; 5 — моно- литный железобетонный ленточный фундамент; 6 — гидроизоляция; 7 — рамный каркас; 8 - кирпичная стена; 9 — крыльцо; 10 — отмостка; — козырек; 12 — облииовка; 13 —- экран; 14 — парапет; 15 — плита парапетная; 16 — па-роизоляция; 17 — утепли- 0 ... 27 28 29 30 31 32 33 ... 87 |
|||||||||||||












