Раздел: Документация
0 ... 26 27 28 29 30 31 32 ... 87 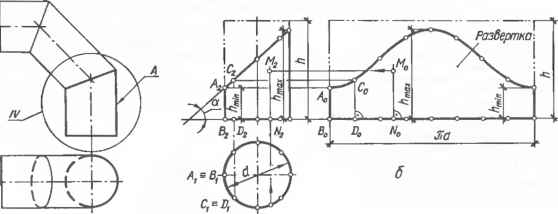 а Черт. 7.3.2. Развертка боковой поверхности прямого цилиндра: а — пример применения; б — построе- ние Черт. 7.3.3. Графическое построение синусоидальной кривой развертки усеченного кругового цилиндра. Черт. 7.3.4. Развертка боковой поверхности цилиндра способом раскатки 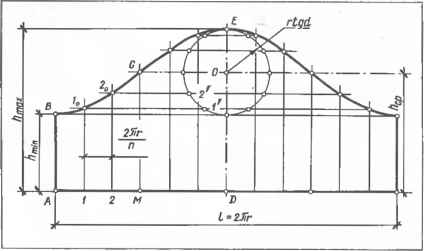 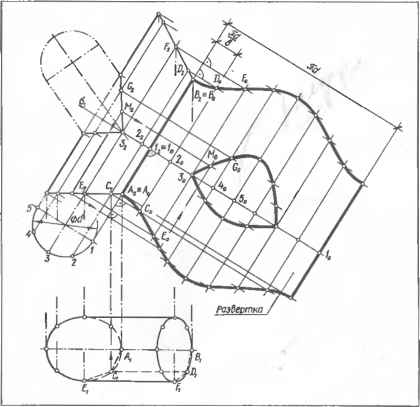 кана (черт. 7.3.2, б). Так как плоскость нормального сечения параллельна плоскости Pj и его горизонтальная проекция сливается с горизонтальной проекцией поверхности, то натуральной величиной периметра нормального сечения является длина окружности основания пй. Для построения точки С0 развертки откладывают отрезок B0D0, равный длине дуги ByDi. Остальные точки развертки строят аналогично. Сплошной линией показана развертка боковой поверхности усеченного цилиндра, штрихпунктирной — полного. Для построения проекций Мх и М2 случайной точки М0 развертки проводят образующую (MoNo)±(BoN0) и отрезок B0N0 откладывают по дуге основания от точки Bl(B1Nt = \BcN0\). при этом m,=Nh \мм = м0лд. 7.3.6.Развертка боковой поверхности прямого кругового цилиндра является прямоугольником (см. черт. 7.3.2, б). Высота И прямоугольника равна длине цилиндра, длина l=nd, где d—диаметр развертываемого цилиндра. Вычисленные размеры развертки следует увеличивать на величину припуска е на резку металла и обработку кромок Под сварку, а в случае тонколистового металла — на образование фальцев. 7.3.7.Точки /0, 20, ... синусоидальной кривой линии развертки поверхности стакана (черт. 7.3.3) можно построить графически. Для этого на горизон- тапьной прямой откладывают отрезок /=2лг и делят его на п равных частей, например 12. Через полученные точки А, 1, 2, ... проводят вертикальные прямые, на крайних из них откладывают длину hmw=\AB\ — длине шейки и на средней hmex = IDE\ — длине затылка и ]DO\=hcp = \GM\. Из точки О как из центра, описывают вспомогательную окружность радиуса, равного г tg а и делят ее также на п равных частей /, 2, ... (л=12). Через деление / проводят горизонтальную прямую и отмечают искомую точку /0 пересечения ее с вертикальной прямой, проведенной через точку / и т. д. Полученные точки В, /0, 20, G ... Е, ... соединяют лекальной кривой линией. 7.3.8.Способ раскатки применяется для построения разверток цилиндрических и призматических поверхностей в случае, когда образующие и одно из оснований проецируются в натуральную величину. На черт. 7.3.4 представлено построение развертки боковой поверхности наклонного кругового цилиндра с вырезом. Горизонтальная проекция выреза не изображена. Горизонтальную проекцию основания аппроксимируют ломаной линией, состоящей из отрезков А ,С,, С,£ ... прямых и проводит ряд прямолинейных образующих [АВ] \\[CD]\\ [EF] ... цилиндрической поверхности. На черт. 7.3.4 изображены только образующие[AtBsb [CiDt]; [C2D2] и [£i£ij; [ЕгЕг]. Участки поверхности между смежными образующими принимают за плоские элементы поверхности ABDC, CDFE, ... Плоский элемент ABDC вращением вокруг (АВ) совмещают с фронтальной плоскостью уровня. При этом фронтальная проекция С8 вершины этого элемента переместится по прямой, перпендикулярной к (А2В2), в положение С0. Точку С0 строят на прямой С2С0 засечкой из А2 радиусом, равным И,С, (так как нижнее основание цилиндра проецируется в натуральную величину, то имеет место равенство IА 2Со = А Ci . Через С0 проводят (C0D0)(/42fi2), так как (CD)\\(AB), и находят точку DC=(C0D0)®(D2DC), где (D2D0)±(A2B2); A2B2D0C0 — совмещенный плоский элемент Вращением вокруг (C0D0) совмещают смежный элемент CDFE с той же фронтальной плоскостью уровня. Для этого проводят (E2E0)J-(A2B2). На (E2F0) из С0 радиусом [CIf ] засекают точку £0. Через £0 проводят (EVF0)\\(C0D0), отмечают F0 = (E0F0)<ЭF2FD, где F2F0±A2B2. Остальные плоские элементы совмещают аналогично. Построенные точки А0, С0, Е0 .... £0, D0, В0 соединяют лекальной кривой. Полученная плоская фигура AoBoD0...CoAo является искомой разверткой. Для построения на развертке контура выреза точки пересечения контура с образующими поверхности, например, G2(E2F2), переносят на соответствующие образующие на развертке, например, G0e (£„£„). Показано также построение для случайной точки М (М2; Л!0) 7.3.9.На черт. 7.3.4 также изображено построение развертки по способу нормального сечения /—2—3 ... (см. п. 7.3.4). Для этого на прямой, совпадаю- щей с a2-L(A2B2), от точки /0 откладывают отрезок /0 — l0 — nd, делят его на равные части (в нашем примере — , через точки 20, 3t деления проводят прямые, параллельные Черт. 7.3.5. Развертка боковой поверхности конуса способом треугольников (А2В2) и откладывают на них отрезки 20С0 = 22С2; 20D0=22D2 и т. д. 7.3.10. Способ треугольников (триангуляции) применяют для построения разверток поверхностей нераз-вертывающихся, конических общего вида и с ребром возврата. В общем случае развертку строят в следующем порядке: 1) в данную кривую поверхность вписывают многогранную поверхность с треугольными гранями; 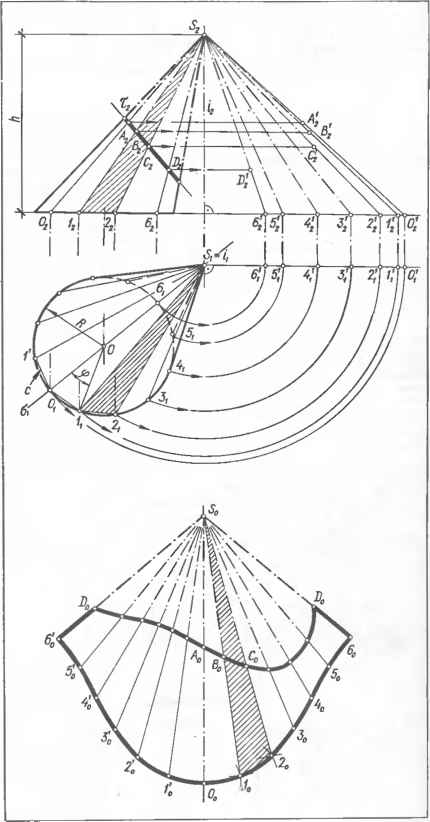 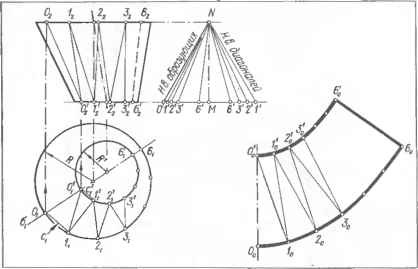 Черт. 7.3.6. Развертка боковой поверхности усеченного конуса с недоступной вершиной. 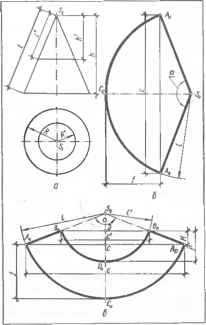 Черт 7.3.9. Косой диффузор: а — исходный чертеж; б - развертка Для этого окружность разбивают на п поверхности.равных частей, например на 12, начи Черт. 7.3.7. Развертка боковой поверхности прямого кругового конуса: а — исходный чертеж; б — при доступной вершине; в — усеченного конуса. Черт. 7.3.8. Прямые диффузоры. 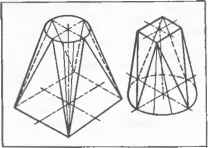 Ф1620 Вид А в50"в50- 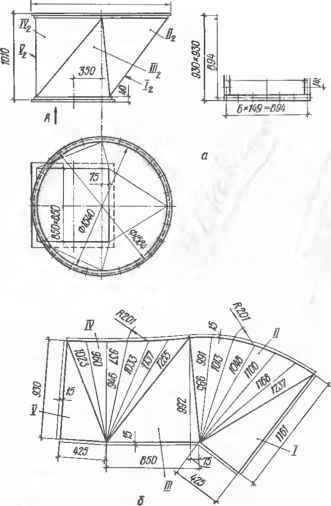 2)определяют натуральную величину всех ребер вписанного многогранника; 3)строят на плоскости чертежа натуральную величину одной грани и к ней, пользуясь смежными ребрами, последовательно пристраивают остальные грани; 4)соответствующие вершины на развертке соединяют плавными (лекальными) кривыми линиями. Полученная плоская фигура является искомой разверткой кривой поверхности При развертывании многогранной поверхности выполняют только операции 2 и 3. Ни практике чаще встречается построение разверток наклонных конусов с круговыми основаниями. Ниже рассмотрены именно такие поверхности. Графическое построение разверток боковых поверхностей любых наклонных конусов при любых очертаниях оснований практически одинаково. Для построения развертки в наклонный конус с вершиной 5 и круговым основанием радиуса R (черт. 7.3.5) вписывают пирамиду с той же вершиной S 0 ... 26 27 28 29 30 31 32 ... 87 |












