Раздел: Документация
0 ... 30 31 32 33 34 35 36 ... 87  Черт. 8.3.8. Штриховка сечений в аксонометрии. При необходимости метрические данные построенной аксонометрии можно определить графически (черт. 8.3.6). Для этого через точки 0и 02 схемы параллельно осям натуральной системы координат проводят прямые OA 1.0В 1. ОС, образующие новую систему координат с началом в 0, откладывают на них равные отрезки 0А = 0В=0С произвольной длины и строят их аксонометрию. Для этого через В, проводят (£,£) III через В2 — (В2£2)П и через Е2 — (ЁгВОйШ- Искомая аксонометрия В= (В,В) х (£2В). Так же строят А и С. Так как в натуре нами принято, что \ОВ\=*х, [ОА] = у и [ОС] = г, то в аксонометрии имеем: [0В\ —х. [0а] = у и [0c]=z. Таким образом, графически определены значения углов аир между аксонометрическими осями. Показателями искажения будут отношения длин отрезков: \0В\\(УА\\0С\ и=-Щ" V==-№T; w=~WcT- 8.3.5. Рассмотрим применение метода параметров аксонометрического про-< жирования при построении аксонометрии здания криволинейного очертания в плане (черт. 8.3.7). Тип аксонометрии — прямоугольная диметрия (см. табл. 8.1.1, п. 3). 1.Построение схемы аксонометрического проецирования. Схему строят на свободном поле чертежа вблизи от исходных ортогональных проекций или непосредственно на них так, как это показано на черт. 8.3.7. Элемент I проводят через А, под углом 25°06/, элемент II через А2 под углом 45°, ось изображения — под углом 55°05 и элемент III — под углом 80°10 к оси изображения. Аксонометрией точки А (Ау; А2) является точка Л = 1 х III. 2.Построение аксонометрии. Для построения аксонометрии кривой задают ряд проекций ее точек (проекции лежат на одной вертикальной линии связи). На черт. 8.3.7 построена аксонометрия С: через С, проведена прямая С,С1, через С2 —прямая С2£2П и через £2 — прямая £2С(1П. Искомая точка С = (С,С) х (Е\С) и т. д. На черт. 8.3.7 также показаны построения аксонометрии В точки В (В,; В2). 8.3.6.Размеры на чертеже, выполненном в аксонометрии, наносят в соответствии с ЕСКД, ГОСТ 2.317—69* (СТ СЭВ 1979—79): выносные линии проводят параллельно аксонометрическим осям, размерные — параллельно измеряемому отрезку. 8.3.7.Штриховку сечений в аксонометрических проекциях выполняют согласно черт. 8.3.8: линии штриховки проводят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны этих квадратов параллельны аксонометрическим осям. ГЛАВА 9. ЧЕРТЕЖИ В ПЕРСПЕКТИВЕ § 9.1. ОСНОВНЫЕ ПОНЯТИЯ И ВЫБОР ТОЧКИ ЗРЕНИЯ 9.1.1.Перспективой называют изображение (чертеж), образованное центральным проецированием фигуры-оригинала на плоскость и удовлетворяющее условиям, учитывающим особенности зрения (см. п. 9.1.7). 9.1.2.Основные понятия и обозначения (черт. 9.1.1): Ii — предметная плоскость, т. е. горизонтальная плоскость, на которой располагается изображаемый предмет (здание, сооружение и т. п.); J] — плоскость карти- ны, перпендикулярная к Д, и служащая плоскостью проекций. Изображение, построенное на такой плоскости, называют линейной перспективой на вертикальной плоскости; о — основание картины является линией пересечения плоскостей J]i и ГГ; S — точка зрения (центр проекций), S, — основание точки зрения (ее горизонтальная проекция), SS,1 =Н—высота точки зрения; [SP) — главный луч (луч зрения, проецирующая прямая) , перпендикулярен к плоскости Ц. Его длину D называют г л а в н ы м р а с Черт. 9.1.1. Аппарат построения перспективы. 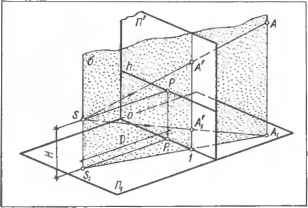 стоянием D = \ SP \ = Р — главная точка картины — точка пересечения главного луча с плоскостью [], Р, — ее основание; \PPl\ = \SSl\=H, h — линия горизонта является линией пересечения плоскости картины [] горизонтальной плоскостью, проходящей через точку зрения S. Линия горизонта h параллельная основанию о картины и проходит через главную точку Р. Расстояние между О и h А — точка-оригинал, Ах — ее основание (план); [SA), [SAy)— проецирующие прямые (лучи зре-ння); о — проецирующая плоскость, проходит через проецирующую прямую; Черт. 9.1.2. Построение перспективы прямой. 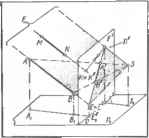 А — перспектива точки-оригинала А; является точкой пересечения проецирующей прямой [SA) с плоскостью картины ]"[; А\ — вторичная проекция точки-оригинала А; является точкой пересечения проецирующей прямой \SAi) с плоскостью картины П, т. е. является перспективой плана Аг. 9.1.3.Основные свойства перспективы и вторичной проекции точки-оригинала А: 1.Перспектива А и вторичная проекция А\ определяют положение точки А в пространстве; 2.Перспектива точки и ее вторичная проекция располагаются на одном перпендикуляре к основанию о картины; 3.Перспектива точки, лежащей на плоскости [], совпадает с самой точкой, а вторичная проекция ее лежит на о; 4.Перспектива точки, лежащей на плоскости J],, совпадает со вторичной проекцией этой точки. 9.1.4.При построении перспективы АВ прямой линии-оригинала АВ (черт. 9.1.2) обычно используют точку Е — картинный след прямой и бесконечно удаленную точку Г прямой, так как построение перспектив Е и F этих точек является простейшим. 1.Точку Е пересечения дан ной прямой с картинной плоскостью {] называют картинным следом прямой. Для построения картинного следа продолжают основание Л,В, данной прямой и отмечают точку Е\ пересечения его с основанием о картины. Через Е\ проводят вертикальную линию связи и отмечают точку Е пересечения ее с продолжением прямой АВ. Так как fef], то перспектива £ = £ (см. п. 9.1.3, свойство 3). Вторичной проекцией является 2.Перспективу / бесконечно удаленной точки F данной прямой линии-оригинала называют точкой сходаперспектив прямых, параллельных данной прямой Параллельные прямые каждого другого направления имеют свою точку схода Чтобы построить точку схода Ff ггерспёктивы данной прямой, через S, проводят, основание луча StF\\\(AiBx) 1 так как [SF )\\(АВ), и отме] чают точку F\ = o(g>[SiF,l)l Через F\ проводят вертикальную линию связи и отмечают точку F пересечения ее с лучом SFго . 3.Перспектива прямой линии проходит через картинный след и точку схода этой линии. Для того, чтобы построить перспективу любой другой прямой, параллельной данной, строят ее картинный след или перспективу любой ее точки и соединяют прямой линией с точкой схода. Эта прямая является искомой перспективой. На черт. 9.1.2 перспектива (АВ) прямой (АВ) проведена через Е и F, перспектива прямой (MN)f(AB) — через К и F. 9.1.5. При вычерчивании перспектив прямых учитывают следующие частные случаи положения точек схода: 1. Прямые линии а, Ь, перпендикулярные к плоскости Г], называют глав-н ы м и ли н и я м и (черт. 9.1.3, а). Точкой с х од а перспектив а, Ь, главных линий является главная точка Р. Перспективой таких линий будет пучок прямых, сходящихся в точке Р. В действительности, когда мы смотрим вдоль улицы, то кажутся сходящимися в одной точке горизонта рель- Черт 9.1.3. Перспектива прямых: а — главных; б — горизонтальных; в — лежащих в проецируемой плоскости; г вертикальных. сы трамвайного пути, бровки Ъ проезжей части улицы, линии а карнизов зданий, которые в натуре взаимно параллельны. 2.Прямые линии с, d, е, ... , параллельные плоскости Д,, называют г о р и-з о нтальными п рямы-мй~(черт. 9.1.3, б). Точки схода перспектив гориз онтальных прямых располагаются на линии горизонта h. Заметим, что основания Си di, в\, .... т. е. горизонтальные проекции любых прямых с, d, е, являются горизонтальными прямыми, лежащими в плоскости J],, поэтому точки схода втр "риных проекций прямых-с\, е\,... (т. е. перспектив оснований) также лежат на линии горизонта h. Если прямая g,... ле-жит в предметной плоскости П,, то ее картинный след £=£ лежит на основании о картины; перспектива такой прямой совпадает с вторичной проекцией этой прямой: g = gt (см. п. 9.1.3, свойство 3). Линии п, лежащие на плоскости J], и проходящие через основание S, точки зрения, а также линии /, пространства, основания которых проходят через Si, изображаются на картине вертикальными прямыми я= / = ..., так как лежат в проецирующих плоскостях a LJ],, проходящих через точку зрения S (черт. 9.1.3, в). 3.Прямые линии, параллельные плоскости ]],— фронтальные линии. Перспективы фронтальных линий параллельны прямым-оригиналам. Любая плоская фигура или линейный угол, образованные этими прямыми, лежат в плоскости, параллельной J], поэтому в перспективе изображаются подобными фигурами. 4.Частным случаем фронтальных линий являются прямые q, г, перпендикулярные к плоскости [],,- вертикальные линии. Их перспективы а, г*, ..., вертикальны, т. е. перпендикулярны к основанию о картины (черт 9.1.3, г) 5.Перспектива z, .... пря,-мой, лежащей в "плоскости ]"[, совпадает с самой прямой. Отрезок такой прямой изображается" в перспективе в натуральную величину! (черт. 9.1.3, г). 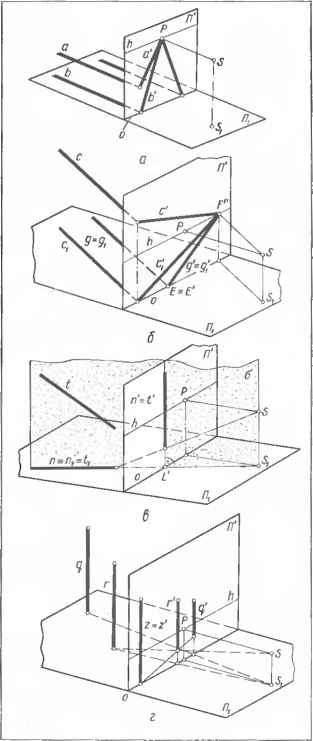 Эти обстоятел ьство прзвг> ляет использ()йат1а прямые, лежащие в плоскости [{, в качестве масштабов: горизонтальные прямые — как масштаб широт и вертикальные — как масштаб высот. На черт. 9.1.4 дан пример использования точек схода перспектив параллельных прямых различных направлений и положений. 9.1.6. Точка схода F перспектив /г, /, .... прямых общего положения, параллельных одному направлению, и точка схода F, вто- ричных проекции этих прямых лежат на одном перпендикуляре к линии горн-зонта h (то же - ко). 9.1.7 При построении перспективы зданий и инженерных сооружений выбор положения точки зрения должен соответствовать действительным условиям рассматривания объекта (действительное положение зрителя, естественный угол зрения) и его формам. Положение точки зрения по высоте Н при расположении зрителя на предметной плоскости при-  Черт. 9.1.4. Использование перспектив прямых разя ичного положения при вычерчивании перспективы застройки территории (пример). Черт. 9.1.5. Перспектива застройки участка про-м ышленн о го об ъ екта. 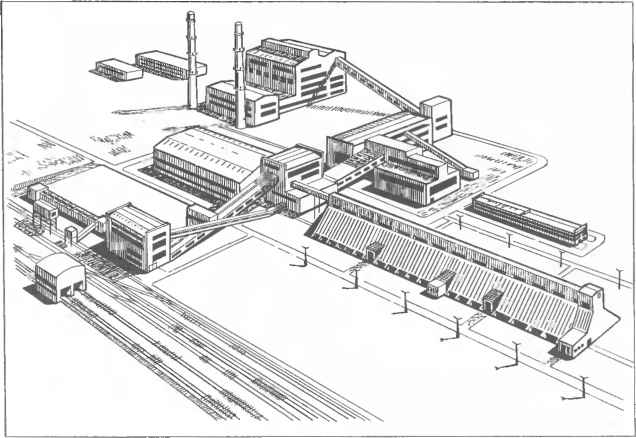 нимают равным 1,7 м (перспектива с нормальной высотой горизонта). В том случае, если здание или сооружение в плане сложной формы или при построении перспективы застройки участка, высоту точки зрения принимают до 100 м и более (перспектива с птичьего полета). Пример такой перспективы приведен на черт. 9.1.5. При расположении здания на возвышенности, а также при изображении отдельных элементов зданий и сооружений, рассматриваемых снизу, точка зрения выбирается ниже предметной плоскости (перспектива при виде снизу). Положение точки зрения в плане выбирают в зависимости от значения угла зрения, форм объекта, действительного положения зрителя и возможности обозрения объекта. Площади, улицы, дворы с симметричной застройкой, интерьеры помещений часто изображают при точке зрения, расположенной на оси симметрии или близко к ней (фронтальная перспектива). При изображении зданий и сооружений точку зрения выбирают так, чтобы были видны главный и боковой фасады одновременно. При этом картинная плоскость и плоскость главного фасада должны составлять угол в 20.-30° (угловая перспектива, черт. 9.1.6). Угол <р между прямыми, соединяющими крайние точки плана изображаемого объекта с основанием точки зрения S,, называют углом зрения. Его принимают равным от 53 до 18°. Наилучший угол зрения 28°. Черт. 9.1.6. Выбор положения точки зрения и основания картины Плоскость главного фасада  0 ... 30 31 32 33 34 35 36 ... 87 |












