Раздел: Документация
0 ... 31 32 33 34 35 36 37 ... 87 При этом отношение главного расстояния D к отрезку /—2, отсекаемому на о сторонами угла, равно 2. Основание Р, главной точки должно находиться на биссектрисе угла зрения (в некоторых случаях в зависимости от форм объекта допускается расположение Р, в пределах средней трети отрезка /—2, заключенного между сторонами угла зрения) . При построении перспективы высотных объектов значение угла зрения в вертикальной плоскости ч]э прини- мают в пределах 20...55° (наилучшие результаты при •ф=30...40°). Угол наклона картины к плоскости горизонта: .три наклоне картины «от зрителя» о = 55.-85°, оптимальное значение со = 73... 82°; при наклоне картины «на зрителя» со=95... 125е, оптимальное значение со=98... 107° [14]. 9.1.8. При построении основания S, точки зрения поступают следующим образом. 1. Вырезают шаблон угла ср=28°. Приложив стороны шаблона к крайним точкам плана, отмечают в вершине шаблона основание Sj точки зрения. Если здание располагается на улице, точку зрения следует выбирать на тротуаре противоположной стороны улицы с таким расчетом, чтобы соседние здания не закрывали изображаемое При этом угол ср может оказаться неравным 28е. Если высотные размеры здания больше размеров в плане, необходимо проверить значение угла зрения в вертикальной плоскости. В зависимости от этого корректируется положение основания точки зрении. 2.Через S, проводят биссектрису угла зрения (основание главного луча). 3.Через ближний к зрителю угол здания проводят основание о картины перпендикулярно к этой биссектрисе и отмечают основание Р, главной точки: Р = оХ XSP,. Если при этом угол между о и плоскостью главного фасада будет выходить за пределы 20...30 , необходимо построение повторить, изменив положение S,. После того, как будет выбрано положение точки зре ния в плане и по высоте, строят перспективу объекта в массах (например, параллелепипеда) и решают вопрос, удачно ли выбрана точка зрения. Иногда после такой проверки возникает необходимость в изменении положения точки зрения. мую, проведенную в плоскости картины (см. п. 9.1.5, частный случай 5). Для того, чтобы на. перспективе q вертикальной прямой от точки А отложить отрезок ЛВ = 1 (черт. 9.2.3), строят "масштаб высот z. Для этого на ли-отрезка нии горизонта h задают случайную точку схода F перспектив горизонтальных прямых, через ¥ и вторичную проекцию q\ данной прямой проводят прямую Fq\, отмечают точку Ех пересечения ее с основанием о картины и через Е{ перпендикулярно к о проводят линию масштаба высот г. Затем 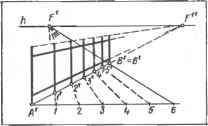 Черт. 9.2.1. Делительный мае- § 9.2. ГЕОМЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ 9.2.1. Деление перспективы прямой на равные или пропорциональные части (применение делительного масштаба) используют при вычегши-вании оконных и дверных проемов на перспективе фасада, перспектив лестниц, оград и т. д. Такое деление ос: HOBaHoTia-известном положении пла-. ниметрии: п а ра л л ел ьн ые прямыечерез F и А проводят прямую, отме- шта® и применение его Оля по-делят стороны угла на пропор-чают точку / пересечения ее с линией строения перспективы ограды. ц и о и а л ь к ы е отрезки. Поэтому,масштаба г, от точки / вверх по z от- чтобы разделить перспективу АВ отрез-кладывают отрезок /—2= \АВ \ =/, пока гор изpjLXiJDiJtнГсш др.дмо й налученную точку соединяют прямой с F п равных, частей, (черт. 9.2J).- лрини-и отмечают точку В пересечения (2F) мают ее за одну сторону линейногос данной перспективой cf. Длина полуугла, другую сторону этого угла про-ченного отрезка АВ перспективы водят через один из концов перспекти-равна / Ш9£~№Щ>тй£#Л[зь$№£в&пьЗаметим, что построенная прямая z линии горизонта и принимают ее заявляется масштабом высот для всех д е л и.т е л ь н ы й м а с ш т a 6~.j Отточкивертикальных прямых, расположенных А на делительном масштабе отклады-в вертикальной плоскости о (F, г). вают требуемое число п равных частей.Признаком принадлежности прямой г например 6, произвольного размера,к плоскости с является расположение Через последнюю точку 6 масштаба ивторичной проекции этой прямой на второй конец В перспективы отрезкалинии /•""£,. Для прочих вертикальных проводят прямую и отмечают точку Fпрямых следует строить свои масштабы пересечения ее с линией горизонта А.высот. В,.качестве, толки F .мс}жнх1 ис.-Эта точка является точкой схода пер-п ользовать имеющиеся точки схода. Черт. 9.2.2. Деление перспективы спектив горизонтальных прямых, парал-лежащие на линии горизонта Айв отрезка прямой общего положе-лельных прямой 6В. Через точку Fтом числе главную точку Р. Измере- ния и точки 1, 2,... делительного масштабание длины отрезка CG вертикальной проводят прямые Fl, F2,... и отмечаютпрямой по его перспективе CG выточки /, 2,... пересечения их с пер-полняют также по масштабу высот: спективой АВ отрезка, делящие этупроводят прямые FC и FG до переперспективу на 6 перспективно равныхсечения с 2, отмечают точки 3 и £,, частей АГ, 12\ 23, ...измеряют отрезок £.3: CC = £i3 = При делении перспективы отрезка на=пт. пропорциональные части, находящиеся9.2.3. ГПз м е р е н и е г о р изонхаль- в заданном отношении / : m : п: .... де-- ных прямых, лят масштаб на пропорциональныеосновано на том части произвольного размера, находящиеся друг к другу в том же отно- в п е р с п е к т иве что вспомогательная прямая Ь, составляющая равные углы со сторонами линейного угла, шении /: m : п : ... . Дальнейшие по- отсекает на этих сторонах равные от-строения выполняют аналогично рас- резки. Практически, при использовании смотренным вышеэтого положения за одну сторону тако- /При делении перспективы АВ отрез- го угла принимают основание о карька прямой общего положения (черт, тинной плоскости (черт 9.2.4). На нем 9.2.2) указанные действия выполняют в натуральную величину (в масштабе со вторичной проекцией А\В\ этого от- картины) откладывают отрезок /. Вто-резка. Полученные точки переносят рой стороной является перспектива а вертикальными прямыми на перспекти- рассматриваемой горизонтальной пря-ву отрезкамой а, лежащей в предметной плос- 9.2.2. Измерения на перспективе верти- кости ]]. кальной прямой производят в масштабе Перспектива Ь вспомогательной пря-картины. При этом используют мае- мой, отсекающей на перспективе а штаб высот г — вертикальную при- данной прямой отрезок, перспективно
Черт 9.2.3. Измерение перспективы вертикальной прямой. Масштаб оысот 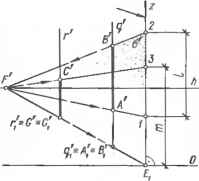 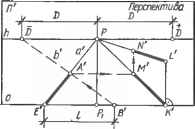 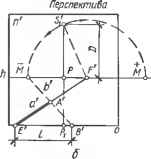 Черт. 9.2.4. Построение точек измерение- а — дистанционных для главных прямых; б аля горизонтальных прямых. равный / проходит через точку схода D (или М), являющуюся точкой измерений. Дистанционная точка D служит" "для измерения перспектив главных линий и является точкой схода персТГеТ\Т1Гв "горизонтальных вспомогательных прямых Ь, составляющих угол 45° с основанием о картины и измеряемой прямой а. Для построения дистанционной точки D (черт. 9.2.4, а) по линии горизонта h откладывают от точки Р главное расстояние D (см. п. 9.1.2). Точкой D удобно пользоваться для измерения главных линий, перспективы которых идут влево, точ-+ кой D — вправо Точка измерений М служит. jj ля измерения перспектив а горизонталь- Черт. 9.2.5. Построение проемов на перспективе фасада здания. А21 23 4 5 6 п 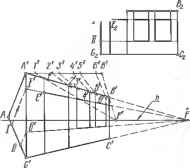 ных прямых а и является точкой схода перспектив Ь горизонтальных вспомогательных прямых Ь, составляющих равные случайные углы с основанием о картины и измеряемой прямой а Для построения точки М измерения горизонтальных линий главное расстояние D откладывают на перпендикуляре к А, восставленном в точке Р, и получают точку S\. Затем радиусом FS\ из точки F, как из центра, описывают полуокружность и отмечают - + точки М и М пересечения ее с линией горизонта. Эти точки являются точками измерения перспектив прямых, параллельных а (черт. 9.2.4, б). Чтобы на перспективе а от картинного следа В отложить отрезок ЛЕ", натуральная длина ЛЕ которого равна /, необходимо на основании о картины от точки Е отложить отрезо с ВЕ = = \АЕ\=1, через полученную точку В и точку D (или М) провести перспективу V вспомогательной прямой Ъ. Прямая Ь отсечет на а искомый отрезок АЕ (черт.. 6.2.4). Перспективы прямых, параллельных Ь (для этого достаточно, чтобы они проходили через D или М), отсекают на о и а перспективно равные отрезки. При этом такие отрезки на основании о натурального размера (в масштабе картины). На черт. 9.2.4 показан перенос размера с перспективы главной прямой а, лежащей в предметной плоскости, на перспективы параллельных ей прямых; отрезки АЕ, МК, NU перспективно равны между собой и равны /. 9.2.4. Построение перспективы элементов фасада здания выполняют с по-мошью целительного масштаба. На ~черт."972.5 изображены фасад A2B2C2G2 здания и его перспектива АВС С. Отрезок А"В перспективы горизонтальной прямой (карниз) делят на части А1, V2,-. перспективно пропорциональные пирине простенков и проемов \Аъ1\, /—2,... . Для этого используют делительный масштаб (AB)\\h, где \ABl\ = \AtB2\,\А11\ = \А21\, /2> = /—2,... строят точку схода /7/=ШВ)ХЛ и перспективы точек деления 1=(ГЕ)Х{АВ). 2(2F)X Х(АВ) (см. п. 9.2.1). Отрезок АС перспективы вертикальной прямой (угол здания) делят на части AV, Г—II,-.. , пропорциональные высот0 дверных и оконных проемов \A2l\, II—III,... . Для построения перспективы оконных и дверных проемов через точки /, 2,... проводят вертикальные прямые, а через + точки V, II,... и точку схода F — перспективы горизонтальных прямых. Точки £,... пересечений этих прямых являются искомыми перспективами углов Е2>... проемов. ГЛАВА 10. ПОСТРОЕНИЕ ПЕРСПЕКТИВ § юл. ПЕРСПЕКТИВА ПЛОСКИХ ФИГУР 10.1.1. При построении перспектив фигур с параллельными сторонамч используют картинные следы и точки схода линий сторон (см. п. 9.1.4). Для примера рассмотрим построение перспективы квадратов, лежащих в предметной плоскости (перспектива паркета, плит и т. п.). 1. Предварительные построения на плане (черт. 10.1.1). Проводят основание о, картины и задают основание точки зрения 5] (см. п. 9.1.7). Из S, проводят основание главного луча (SPi)Xo, и отмечают основание главной точки Р] —(SiPi) х 0\. Точки схода линий, идущих влево, обозначают знаком « - », например, F, идущих вправо — знаком «+», например + F, без знака штрих. Для построения точек схода перспектив параллельных сторон квадратов через S, проводят + прямые SiFi\\AiBu S\Fi\\AtCl и отме- - -+ чают точки Fi =(SFi)X Oi, Ft = + = {S\F\)X,o1, являющиеся основаниями точек схода. 2. Предварительные построения на картине (перспектива). Проводят горизонтальную прямую о — основание картины — и параллельно ей — линию горизонта п. Примерно на середине h задают главную точку Р, проводят (РР) 1 о и строят на о основание Я, главной точки. - + Строят точки схода F и F перспектив горизонтальных прямых. Для этого на линии горизонта h от точки Р откла- дывают отрезки: влево PF=P\F\ и + + вправо PFPjF,. 3. Построение перспективы прямой Л[С. Отмечают точку / = = (i4iCi)XOi, измеряют отрезок 1РЛ (см. план) и на о перспективы от точки Р, откладывают отрезок 1РЛ = 1Р1. Точка / является перспективой картинного следа линии <4,С,, точка F — точкой схода перспективы этой линии, + так как (SiF,)\\(A,Ct). Прямая IF является искомой перспективой прямой Л, С,. Для построения перспективы прямой B\D\\\A\Ci строят след 2 и соединяют + его с F и т. д. Заметим, что последовательно откладывая на о перспективы отрезок /—2: снятый с плана, и соеди- + няя полученные точки с F, строят перспективы ряда сторон квадратов, параллельных (i4,C). 4. Построение перспективы прямой C£)i- Отмечают точку 3 = =(CZ)i)xoi плана, на о перспективы откладывают отрезок Pt3, получают картинный след 3. Искомой перспективой является прямая 3F, так как (S.F.WGD.) и т. д. Так как вершина A,=(A,Bi)X.(A,C,), то перспективой этой вершины явля-- + ется точка A—(4F)X,(lF), аналогич- - + но B=(4F)X(2F) и т. д. 10.1.2. Вбольшинстве- £лучаев перспективой окружности является эллипс, в частном случае при плоскости окружности, параллельной J] — окружность, при точке зрения, лежащей в плоскости окружности,— отрезок прямой. При построении небольшого размера перспектив окружностей применяют споссГб восьми точек. Пусть требуется построить перспективу окружности диаметра d, лежащей в предметной плоскости (черт. 10.1.2). На картине проводят Л, о и задают Р и D (см. п. 9.2.3). На о задают точку d а и откладывают — влево и вправо от нее. Полученные точки Ь и е и точку а соединяют прямыми с Р. На (аР) задают перспективу А центра окружности и проводят прямую AD> засекающую (ЬР) и (еР) в точках С и Е — перспективах вершин описанного квадрата. Через эти точки проводят горизонтали, засекающие еще две вершины — /и В. Точки ], 2 пересечения (аР) с (ВЕ) и (Gl) и точки 3, 4 пересечения горизонтали, проходящей через А, являются перспективами четырех точек окружности. Еще четыре точки строят на диагоналях квадрата. Для этого План
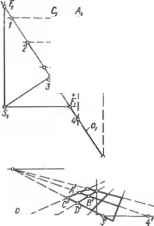 Т У р, Черт. 10.1.1 Построение перспективы паркета. из а и Ь под углом 45° к о проводят две прямые, пересекающиеся в точке /, и из а радиусом al делают засечки п и п на о. Прямые пР и пР пересекут диагонали в искомых точках 5, 6, Т и 8. Лекальная кривая (эллипс), проведенная через построенные перспективы /, 5,... 8, 1 точек окружности, является искомой перспективой окружности. На чертеже построена перспектива окружности диаметра d, лежащей в вертикальной плоскости, перпендикулярной к ["[. Построения выполнены аналогично. 10.1.3. При делении перспективы окружности на равные части построения выполняют в следующем порядке (черт. 10.1.3). Через О параллельно линии горизонта h проводят перспективу АВ диаметра. На диаметре АВ вычерчивают полуокружность и делят ее на требуемое число равных частей, например 6 Полученные точки /, 2,... проецируют вер- 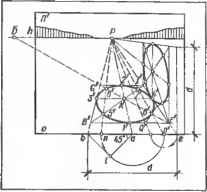 Черт 10.1.2. Построение перспективы окружности по восьми точкам.
Черт. 10.1.3. Целение перспективы окружности на равные части. тикальными прямыми на АВ и отмечают точки 1\, 2\,... . Через главную точку Р и точки /,, 2\ проводят прямые и отмечают точки /, 2,... пересечения их с перспективой п окружности. Эти точки делят перспективу окружности на перспективно равные части А1\ Г2.... (в данном случае на 12). § 10.2. МЕТОДЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ 10.2.1.В практике построения перспек-тив архитектурных объектов обычно каким-либо методом строят изображение в основных массах, т. е. вычерчивают описанные параллелепипеды, охватывающие основные объемы, и по ним судят о правильности выбора положения точки зрения, удачно ли скомпонована перспектива "в целом и т. д. После решения этих вопросов непосредственно на картине детализируют изображение, используя построения, рассмотренные в § 9.2, 10.1. 10.2.2.Метод следа луча (радиальная перспектива) применяют при построении фронтальных перспектив, площадей и-улиц с двусторонней симметричной застройкой, внутренних дворов, перспектив интерьеров; а также перспектив объектов, имеющих в плане непрямые углы. Исходные документы: фасад и план, вычерченные в одинаковом масштабе и расположенные в проекционной связи, генеральный план в любом масштабе (для выбора положения точки зрения). Геометрическая основа: перспективой точки является точка пересечения луча зрения с плоскостью картины. Пример. Построить перспективу здания с криволинейным планом (черт. 10.2.1). Решение. 1. Предварительные построения на плане — выбирают положение основания Sj точки зрения (см. п. 9.1.7). Для этого параллельно оси х12 проводят основание о, картины. Этим задают плоскость картины J], параллельную фронтальной плоскости {]2- Отмечают точку Р, пересечения о, с осью симметрии и с учетом обеспечения оп тимального значения ср угла зрения, а также расположения существующих я проектируемых зданий задают на этой оси искомое основание Si; на фасаде — основание картины о=х12 Проводят на фасаде линию горизонта h\\xi2 и отмечают главную точку Р кар- тины в точке пересечения h с осью симметрии (P=S2); на перспективе — отображение плоскости картины HJIj, то о, ft и Р фасада одновременно являются элементами перспективы. 2 Для построения перспективы А точки/4 (Л,; Аг) здания через S, и Л, проводят прямую — горизонтальную проекцию луча зрения — и отмечают точку /=Sjy4i)xoi плана. Через точку / проводят линию связи (1А)±о1. Через P=S2 и А2 проводят прямую — фронтальную проекцию луча зрения — и отмечают искомую перспективу А = =\РА2)х(1А). 3.Для построения перспективы В случайной точки В (В,; В2) с помощью вертикальной линии связи, проведенной через горизонтальную проекцию В, случайной точки плана, строят фронтальную проекцию В2 (можно произвести в обратном порядке). Дальнейшие построения выполняют так же, как в п. 2 и т. д 4.Соединяют линиями перспективы соответствующих точек. Полученное изо- 0 ... 31 32 33 34 35 36 37 ... 87 |
||||||||||||||||||||||||||












