Раздел: Документация
0 ... 34 35 36 37 38 39 40 ... 87 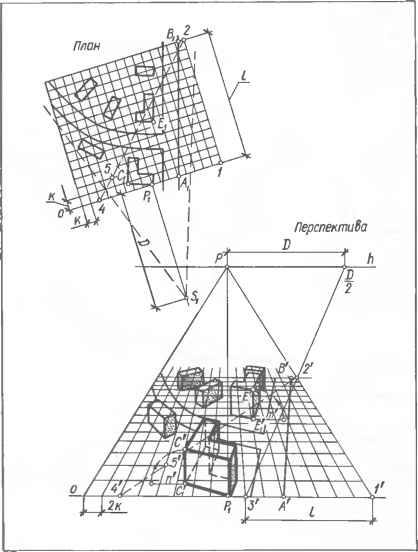 тиве. По такой перспективной сетке, как по своеобразной координатной сетке, строят перспективу объекта. Пример. Построить перспективу застройки участка (черт. 10.2.13). Решение 1. Предварительные построения: на плане — выбирают положение оснований точки зрения S,, картины о и главной точки Рх (построения см. в п. 9.1.7). Принимают основание о за одну сторону и вычерчивают сетку равных квадратов со стороной k или на кальке тушью вычерчивают такую сетку, накладывают ее на план так, чтобы одна сторона совпала с о, и закрепляют неподвижно кнопками или липкой лентой; на перспективе — вычерчивают основание о картины, основание Р, главной точки, в принятом масштабе увеличения, например 2:1, откладывают \Р,Р\—2Н, проводят линию горизонта А о и строят на ней сокращенную в D 2 раза дистанционную точку — , для чего откладывают Р D. Вы 7 Через точку Р " проекции А\, В\ С\,... проводят лучи а, Ь, с,... пучка Р лучей — определителей перспектив вершин. Пучок Р лучей и конфигурация картинных следов образуют определитель перспектив данного здания. II. Построение перспективы: начинают с задания желаемого отклонения от вертикали перспективы CD ближнего к точке зрения ребра CD, для чего через след 5 проводят эту перспективу пределах между лучами с и dy затем из точек С и D проводят перспективы соответствующих пар горизонтальных прямых в свои картинные следы в пределах между соответствующими лучами пучка Р и т. д., пока не построят перспективу всего габаритного объема здания. Для разбивки перспективы габаритного объема здания на этажи используют делительный масштаб с центром соответствия в точке Р и детализированные в пропорциях фасада картинные следы видимых стен здания. 10.2.7. Метод перспективной сетки применяют для построения перспективы планировки больших участков при наличии в плане большого количества кривых линий (планировка парков, скверов и т. п.), при высокой точке зрения, при необходимости быстрого построения перспективы и в Черт. 10.2.13. Метод перспективной сетки. случаях, не требующих большой точности. Исходные документы: генеральный план участка, развертки застройки улиц, площадей, планы и фасады зданий, сооружений и т. п. Геометрическая основа: на исходный план наносят сетку квадратов и одним из известных способов вычерчивают перспективу, которая служит основой для вычерчивания перспективы плана и определения перспективных высот. Наиболее удобна сетка из прямых, параллельных и перпендикулярных к картинной плоскости, так как перспективы первых параллельны основанию картины о, а перспективы вторых проходят через точки деления о и сходятся в главной точке Р. В некоторых случаях перспективную сетку наносят в виде прямых трех направлений: прямые двух направлений соответственно параллельны двум взаимно перпендикулярным горизонтальным линиям объекта, третьего — вертикальны. Расстояния между смежными прямыми перспективно равны. Таким образом, прямые линии сетки, пересекаясь, образуют ячейки, представляющие собой кубики в перспек- черчивают перспективу сетки с увеличенной в 2 раза стороной квадрата. Для зтого на о от Р, в об* стороны откладывают отрезки, равные 2k. через полученные точки и главную точку Р проводят прямые, являющиеся перспективами сторон сетки, перпендикулярных к о и к []. Для построения перспективы сторон сетки, параллельных о, на перспективе (1Р) откладывают отрезок 12, перспективно равный 21: для этого по о откладывают отрезок 13=1, проводят прямую 3 и отмечают точку 2= \3 х {1Р). Затем проводят перспективу (24) диагонали (2—4) и через точки 5,... пересечения ее с построенными ранее перспективами прямых, перпендикулярных к о, проводят параллельно о искомые перспективы сторон сетки. 2. Построение перспективы объекта. Положение характерных точек Аи В,, С1?... объекта с сетки плана переносят по клеткам на сетку перспективы Построенные таким образом перспективы А, В, С,... точек соединяют линиями в соответствующем порядке. По фасадам, разверткам и т. п. измеряют высоты т, характерных точек объекта (или в целом зданий, сооружений). Для откладывания высот в перспективе, например, п — для точки Сит — для точки Е — через вторичные проекции С\ и Е\ этих точек проводят горизонтальные прямые и на них в масштабе сетки 6 этом месте откладывают пит единиц. Полученные отрезки п и т являются перспективными высотами; их эткладывасот на соответствующих вертикалях: п= \C\C\, т = \Е\Е\ и т. д. Перспективы высот можно определить с помощью :бо..-,у вой стены», задаваемой главной прямой ОР и масштабом высот Се е ен : .j !-. е iк а вают соединение перспектив точек соответствующими линиями. ГЛДВА 11. ЧЕРТЕЖИ В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ § ИЛ-ОСНОВНЫЕ понятия И ИЗОБРАЖЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 11.1.1.Обозначения геометрических фигур в проекциях с числовыми отметками: нижний числовой индекс, поставленный у изображения или обозначения проекции точки, линии, плоскости, означает числовую отметку этой точки, линии, плоскости, например, Аъ, а17. э, ав; основная плоскость проекций — J] с добавлением нижнего числового индекса, указывающего на отметку этой плоскости, например По- П120. —; уклон —/, интервал — /; масштаб уклонов плоскости — сс (как и плоскость) с добавлением нижнего индекса с, например, а/, Э< — - 11.1.2.Параллельные, проекции точек на любуюплоскость проекций, сопровождаемые числами, определяющими удаление точек-оригиналов от их проекций, называют проекциями с числовыми отметками. Размер удаления измеряют по направлению проецирования. В архитектурно-строительной практике распространены прямоугольные проекции на горизонтальную плоскость проекций. В этом случае числовая отметка указывает расстояние от точки-оригинала до плоскости проекций. 11.1.3.Строительные чертежи котлованов, насыпей, выемок, каналов, плотин и других земляных сооружений, чертежи организации рельефа местности и т. п. выполняют в проекциях с числовыми отметка-м и. 11.1.4.В проекциях с числовыми отметками чертеж фигуры состоит из ее изображения и числовых отметок характерных точек и элементов этой фигуры: точки задают их проекциями и числовыми отметками, например, Л4, В-з, С0.... (черт. 11.1.1); прямую линию задают ее проекцией и отметками двух точек (черт. 11.1.2). о С0 Пв 1 0 1 2 3 4 5м Черт 11.1 1. Чертежи точек А, В и С в проекциях с числовыми отметками.
Черт. 11.1.2 Чертеж отрезка А В в проекциях с числовыми отмотками. Натуральный размер отрезка АВ и угол наклона ф° прямой к основной плоскости П0 определяют по его чертежу способом прямоугольного треугольника (см. [16, с 45]); плоскость может быть задана так же, как и в ортогональных проекциях-. Наиболее удобным способом задания плоскости в проекциях с числовыми отметками является задание ее масштабом уклона, что наглядно характеризует положение плоскости в пространстве (т. е. ее простирание и падение) и удобно для построения горизонталей (черт. 11.1.3); многогранныепо- верхности в проекциях с числовыми отметками задают проекциями ребер с указанием отметок вершин. В качестве примера на черт. 11.1.4, с изображена проекция S3A0B0C0 пирамиды SABC. Точки А, В и С имеют отметки О, следовательно, основание пирамиды лежит на основной плоскости П0- Чтобы провести горизонтали / и 2 плоскости грани, например  5 01020м Черт 11.1.3 Чертеж плоскости а в проекциях с числовыми отметками. Черт. 11.1.4. Способы задания поверхностей: а, б — многогранных — проекциями соответственно сетки, основания и уклонами боковых граней; в — кривой каркасом горизонталей. SAB, градуируют ребра [S3A0] и [S3B0] и соединяют прямыми точки с одинаковыми отметками. Многогранные поверхности также задают проекцией и отметкой одной из граней (например, дно котлована, бровки земляного полотна и т. п.) и уклонами других граней (например, откосов котлована, насыпи или выемки земляного полотна и т. п.), что удобно при решении инженерных задач, связанных с определением границ и объемов земляных работ (черт. 11.1.4, б); кривые поверхности в проекциях с числовыми отметками задают проекциями горизонталей (линиями пересечения поверхности горизонтальными плоскостями) с указанием их отметок (черт. 11.1.4. в). Такой способ задания поверхности является наиболее простым и удобным, особенно для изображения неправильных (случайного вида) поверхностей, так называемых графических, или в применении к земной поверхности — топографических. 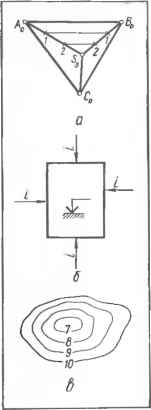 11.1.5. При геометрических операциях на прямых линиях используют понятия и н-тервал и уклон прямой линии. На черт. 11.1.5 изображена прямая А В и ее проекция (Л,.6В3>4) на основную плоскость П0. Параллельно проекции прямой и, следовательно, параллельно плоскости По проведена линия уровня 2 и выше нее на расстоянии, равном одной единице длины,— линия уровня 3. Точки С и D пересечения прямой с линиями уровня имеют отметки 2 и 3. Расстояние между проекциями С2 и D3 является интервалом прямой АВ. Интервалом / прямой называют горизонтальное расстояние между такими двумя точками прямой, разность отметхж которых равна единице-ГГоризонтальное расстояние <• между двумя любыми точками А и В прямой называют заложением L, или горизонтальным про-ложением, а расстояние по вертикали между этими точками — превышением /. Численно интервал прямой равен отношению заложе- 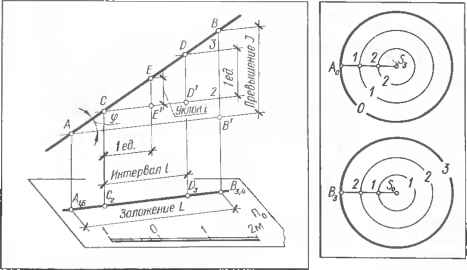 Черт. 11.1.6. Горизонта- Черт. 11.1.5. Графине- вала I и уклона i пря- ли поверхности прямого ское определение интер- мой.кругового конуса. 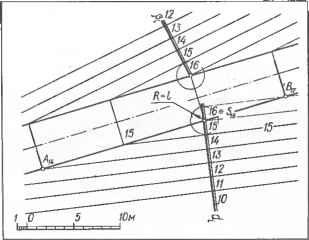 ни я к превышению: — — Величину превышения, приходящуюся на заложение, равное единице, называют /клоном i прямой, который численно равен отношению превышения к заложению: 1=х- Уклон пинии является величиной, обратной ее ин- . 1 тервалу i— — . f 1.1.6. Проградуированную проекцию линии наибольшего уклона плоскости а называют масштабом уклона плоскости и обо- значают а,. Проекции го-ризонталей плоскости и ее след А перпендикулярны к линии масштаба уклона этой плоскости. Интервал / плоскости равен интервалу линии наибольшего уклона ее и является расстоянием между проекциями смежных горизонталей этой плоскости. Величина уклона i плоскости обрати;?: величине ее интервала /. 11.1.7. Проекции горизонталей прямого кругового конуса используют в качестве вспомогательных линий при построении горизонталей откосов насыпей и выемок, плоскостей заданного уклона, проходящих через Черт. 11.1.7. Построение горизонталей плоское! ей откосов насыпи. заданные прямые общего положения, и т. п. На черт. 11.1.6 изображены два одинаковых круговых конуса: один, стоящий основанием на плоскости По (проекция его основания — окружность с отметкой О, проекция вершины — точка S3), и другой, опирающийся вершиной на ту же плоскость (проекция его основания — окружность с отметкой 3, проекция вершины точка S0). Высота конусов равна трем единицам. Для построения горизонталей поверхности проводят образующие [S3j40) и (50В3) конусов, градуируют их и через полученные точки /, 2 из проекций вершин 58 и 50, как из центров, описывают окружности, являющиеся искомыми проекциями горизонталей, с отметками / и 2. Из рассмотренных построений следуют выводы: 1.Проекциями горизонталей прямого кругового кинута яв-ляются концентрические окружности. 2.Радиусы смежных горизонта I.ей, разность отметок кото рых равна единице, Глава 11. Чертежи в проекциях с числовыми отметками115 отличаются на один интервал образующей конуса. 3. Разность отметок горизонтали конуса и его вершины равна числу интервалов, содержащихся в ради у-се этой горизонтали. Например, если длина радиуса равна двум интервалам, отметка горизонтали на две единицы больше (или меньше) отметки вершины Пример. Построить горизонтали откосов насыпи земляного полотна автомобильной дороги на прямом участке. Уклон откосов i— = 1 : 1,5. На плане заданы, бровки земляного полотна (черт. 11.1.7). Земл яное полотно представляет собой призму, его откосы являются гранями, а бровки — боковыми ребрами призмы. Задача сводится к ноет юс нию масштаба уклонов плоскости (откос), проходящей через заданную прямую {бровка i! и имеющей заданный уклон. Решение. 1. Градуируют бровку-/?,?. Отметки 14, 15, 16 и 17 переносят на бровку северного откоса. 2. Вычисляют интервал плоскости откоса /=-г- = i = 1,5 м. Какую-либо точку бровки, например 16, принимают за вершину Sl6 конуса и из нее, как из центра, радиусом 1,5 м (т. е. равным одному интервалу), описывают окружность, являющуюся вспомогательной горизонталью конуса (см. черт. 11.1.6). Так как /?=/, отмотка этой горизонтали на единицу меньше отметки вершины и равна 15. 3- Через точку 15 бровки проводят прямую, касательную к вспомогательной горизонтали 15 конуса. Эта прямая является горизонталью 15 южного откоса насыпи. Через точку 16 перпендикулярно к горизонта, ли 15 проводят линию масштаба уклона сс, плоскости этого откоса, градуируют ее интервалом /=1,5 м и через полученные точки 17, 16 14... перпендикулярно к сс, проводят искомые горизонтали, которые изображают плоскости откосоь насыпи 0 ... 34 35 36 37 38 39 40 ... 87
|
