Раздел: Документация
0 ... 13 14 15 16 17 18 19 ... 78 зависеть от этих параметров и характеризоваться вектором D(f, 8, Z), где вектор Z представляет параметры среды распространения. Для определения координат источника сигнала необходимо теперь найти минимумы функции к G(8,Z)= X V,o,/)D(/,e,Z)2(5.31) i = N + 1 не только по 8, но также и по Z. 5.3.4. Результаты экспериментальных исследований Цдя иллюстрации рассмотренного метода здесь представлены результаты эксперимента с очень простой антенной решеткой при гидролокации сигналов на фоне шума. Использовалась линейная 5-элементная эквидистантная (с межэлементным расстоянием 1 м) решетка, расположенная в горизонтальной плоскости. Производилась оценка МВСП в диапазоне частот 850 Гц с разрешающей способностью 5 Гц при накоплении 10 последова- 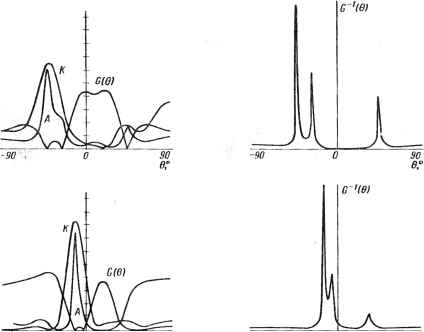 ло090-30О30 е°в° а)6) Рис. 5.6. Экспериментальные диаграммы изменения звукового ноля под водой в зависимости от угла визирования 0 дли трех источников сишалов: а) - классическая диаграммообразующая схема (К"); адаптивная решетка (А); метод ортогонального подпространства С7(0); б) - диаграммы С" (0)  о 0,5 1,5 т о)
-900W
-90090о
в; Рис. 5.7. Экспериментальные результаты приема акустических сигналов трех источников: а - диаграммы изменения звукового поля в зависимости от угла визирования в для параметра когерентности шума т=0,5 (классическая диаграммообразующая схема (К*); адаптивная решетка (А}; метод ортогонального подпространства О(0); б - диаграмма изменения собственных значений в зависимости от параметра т (сходимость двух наименьших собственных значений -наблюдается при Ш-0,4); в - диаграммы значений функции О"1 (0) в зависимости от угла визирования в (наилучшие результаты при т=0,4 и 1,5) тельных оценок спектра. Использовались три источника сигналов. Графики изменения напряженности звукового поля в зависимости от угла визирования для классической диаграммообразующей схемы, адаптивной антенной решетки и для метода ортогонального подпространства G(6) приведены на рис. 5.6. Предполагалось, что фоновый шум некогерентен. Другая ситуация, при которой по-прежнему присутствуют три источника, но предпринята попытка смоделировать пространственную когерентность фонового шума, проиллюстрирована на рис. 5.7. Выбрана модель шума морской поверхности, описываемая соотношением (5.16). Нетрудно заметить сходимость для двух наименьших собственных значений при т = 0,4. Очевидно, что три наибольших собственных значения соответствуют трем источникам сигналов. Тогда согласно данным рис. 5.7,в наилучший результат достигается при /« = 0,4. Эти эксперименты "на море" иллюстрирую! преимущества методов высокой разрешающей способности перед методами исследования с помощью классической и адаптивной антенной решеток. 5.4. РЕАЛИЗАЦИЯ МЕТОДА ВЫСОКОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ В этом разделе описывается реализация наиболее общей структуры методл ВРС и дастся оценка ее вычислительной сложности. 5.4.1. Общая структура Общая структура алгоритма, реализующего метод ВРС, показана на рис. 5.8. Его можно разделить на три основных этапа. Если первый и третий этапы очевидны, то второй этап (включающий операцию фокусирования) требует вычислений новых типов. Первый этап: обработка входных данных. На этом этапе осуществляется предварительная обработка входных данных для получения величин, необходимых для реализации ВРС, а именно оценок МВСП. При этом используются обычные операции. На первом шаге выполняется преобразование Фурье выходных сигналов А/ элементов антенной решетки. Затем, если число частотных составляющих при спектральном анализе равно L, то выбирается L идентичных параллельных каналов обработки. Этот параллелизм сохраняется в структуре общей схемы обработки. Второй шаг обработки входных данных сводится к оценке МВСП с помощью соотношения (5.14): I in+i ip г,,Ш = - I х,-(./;,)х;+ш. Г I яР Вектор (матрица-столбец) Х,-(/с) имеет N составляющих, являющихся выходными отсчетами преобразования Фурье на частотах /е(е€[1, L]). Вычисления выполняются путем матричного умножения и накопления. При типовой обработке сигналов антенной решетки оценивание МВСП обычно не производится; исключение составляет адаптивная обработка От элементов антенной решетки 00/77 3 БПФ ... L оценка мвеп L Часть U К предварительная обработка ( входных сигналов вычисление собственных значений и собственных Векторов * Определение подпространства источников и ортогонального подпространства
Вычисление собственных значений Гсв зави- симости от m Оценка параметров когерентности Л фонового шумат0 Часть 2: К специфические \ вычисления ИЛИ: метод ортогонального подпространства ИЛИ: метод подпространства источников -система уравнений -подгонка модели мвеп источника к оценке этой матрицы -модифицированные методы максимального правдоподобия или максимума энтропии -1 I Часть 3: > Оценка параметров ( источника т.) Решение задач гидролокации Рис. 5.8. Общая структура алгоритма, реализующего метод высокой разрешающей способности сигналов решетки в частотной области на основе непосредственного обращения оценки МВСП. Второй этап: специфические вычисления при методе ВРС. Основные вычисления метода ВРС являются новым типом обработки сигналов антенной решетки и обычно сводятся к вычислительным процедурам линейной алгебры. Они состоят в нахождении собственных значений для оценки МВСП. 103 При этом можно использовать различные методы. Однако, вероятно, наиболее подходящим для эрмитовых матриц является метод, при котором входная матрица сначала приводится к трехдиагональному виду Гт с помощью метода Хаусхолдера, а затем используется QR-метод. Эта процедура широко описана в литературе [10]. Здесь рассмотрим ее основные этапы. Преобразование к трехдиагопальной форме осуществляется с помощью аналогичных N- 2 шагов Гт = % 2 - • • U,ГЦ ... VN 2 - Uf U.(5.32) Матрицы а следовательно, и Uявляются унитарными. Они должны вычисляться на каждом шаге. QR-метод основан на рекурсивном алгоритме, с помощью которого матрица Гт приводится к верхней треугольной форме при бесконечном увеличении числа итераций. Трехдиагональная матрица запоминается. Приведение к треугольному виду получается с помощью унитарных преобразований подобия, такого же, как при получении предыдущей трехдиагональной матрицы. В результате собственные значения и собственные векторы Г могут быть легко получены из собственных векторов верхней треугольной матрицы. Собственные значения и собственные векторы верхней треугольной матрицы вычисляются прямым способом. На первой итерации Гт приводится к верхней треугольной матрице Rt с помощью аналогичных Л- 1 шагов: R, = U , ...U}fT = Q,fT.(5.33) Матрицы U?, а следовательно, и Qj являются унитарными. Пусть Г, = Rj Qj. На второй итерации Г, приводится к верхней треугольной матрице R2 = -Q2i, из которой получается Г2 =R2Q2, и т.д. Можно показать, что нар-й итерации Г = R Q = Q+ ... Qtf Q, . .. Q = W+f W .(5.34) V VP PтP P P Итерации прекращаются при достижении заданной точности. Матрицы О и Wp будут унитарными. Собственные значения Г будут равняться собственным значениям Тр, находящимся на главной диагонали. Если обозначить через V собственные векторы матрицы Тр, то собственными векторами матрицы Г будут UW V. Собствешшю векторы и значения вычисляются на двух основных шагах обработки, обеспечивающей ВРС. Первый шаг сводится к оценке параметров m0(fe) пространственной когерентности фонового шума. Следующие операции должны выполняться для некоторого заданного числа значений моделируемого параметра rn: а)комплексное умножение матриц для вычисления матрицы [соотношение (5.23)] Гси <fe> ™) = С Ое> т>ГиС+ (fe, т);(5.35) б)вычисление собственных значений матрицы Тсп (fe, m); 104 в) расчет простой функции собственных значении для нахождения оценки I Второй шаг сводится к построению подпространства сигналов и его ортогонального дополнения. Для выполнения этой операции потребуются собственные значения и собственные векторы матрицы Гсп [fe, m0(fe)]: подпространство сигналов определяется K(fe) собственными векторами, связанными с K(fc) наибольшими собственными значениями, а ортогональное подпространство - остальными [N- К (fe) ] векторами. Как показано в [8],K(fe) определяется простой функцией собственных значений. Третий этап: оценка параметров источников сигналов. Оценка параметров источника для каждого элемента разрешения по частоте может быть получена различными методами. Могут использоваться подпространство сигналов или ортогональное подпространство. В каждом случае сложность вычислений в большей или меньшей степени зависит от использования неизвестных параметров среды распространения Z в модели вектора источника. I.Метод ортогонального подпространства. Оценки углового положения источников определяются значениями в, связанными с K(fe) максимумами функции (5.31) параметров 8 и Z : S v;+0(/e)D(/;,e,z)2l \(5.зб) В тех случаях, когда число параметров 8 и Z невелико, в частности когда модель не включает параметры среды распространения, максимумы могут быть определены с помощью последовательного просмотра значений (/е, 8, Z) с шагом по 8 и Z, зависящим от разрешающей способности. Эта операция основана на получении скалярных произведений комплексных векторов. Это очень похоже на классическую диаграммообразующую схему, однако требует большого объема вычислений из-за нахождения [N-K(fe)] скалярных произведений и из-за малых приращений параметра 8, необходимых при высокой разрешающей способности. 2.Методы подпространства сигналов. Существует несколько методов, основанных на использовании подпространства сигналов. В работе [4] описан метод, в котором не учитываются параметры среды распространения Z и который также основан на поиске максимумов функции от скалярных произведений комплексных векторов. Метод [1] основан на подгонке модели МВСП сигналов к оценке этой матрицы также без учета параметров среды распространения. В работе [3] показана возможность введения параметров среды распространения в модель, в результате чего получается система NK(Je) уравнений с NK(fe\ неизвестными, если число неизвестных параметров распространения Z =JFC(fe) [N-K(fe) +7/2]. Этот метод в общем случае требует решения системы нелинейных уравнений. Сложность вычислений зависит от структуры вектора модели источника сигнала. 105 0 ... 13 14 15 16 17 18 19 ... 78 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||












