Раздел: Документация
0 ... 12 13 14 15 16 17 18 ... 78  ~sse° -3>-W ~9-0-Je7 a>6)B) Рис. 5.3. Диаграммы значений функции С- (в) для шумового поля, характеризуемого зависимостями на рис. 5.2 (метод ортогонального подпространства) о)т-о,2; б)т=0,8; в)/и=0,5 диаграммы. Первая из них теоретическая. Три другие соответствуют различным условиям пространственной когерентности фонового шума, характеризуемым значениями параметра т, равными 0,5; 0,2 и 0,8 соответственно. При /?? = 0,5 согласно принятым условиям МВСП является единичной матрицей. И действительно, диаграмма H(Q) в этом случае идентична теоретической диаграмме. При /?г=0,2 отличие Н(в) от теоретической диаграммы незначительное. Однако при ш = 0,8 диаграмма совершенно отличается от предыдущих. На рис. 5.3 для тех же исходных данных представлены результаты вычислений при использовании метода ортогонального подпространства. Показанные диаграммы являются функциями С1 (в) (см. (5.13)); при этом наблюдаются пики, а не минимумы. Эффективность здесь несколько снижается, когда матрица пространственной когерентности фонового шума становится отличной от единичной (/?г0,5). Адаптация к пространственной когерентности фонового шума [9]. Когда матрица пространственной когерентности фонового шума 1(f) известна и не является единичной, можно показать, что все сводится к предыдущей проблеме. Действительно, поскольку J (/) является эрмитовой положительно определенной матрицей, то можно найти матрицу C(f), для которой C(/)J(0C+(/)=I.(5.18) Когда исходная МВСП преобразуется с помощью C(f), получается выражение Гс(0 =С(/)Г(/)С+(/) =a(/)C(/)J(/)C+(0 + + £ Ъ(ЛС(ЛЦфЦГфС+(/).(5.19) Учитывая, что С(Г)Ц (J) - вектор (который можно обозначить через D - (f) и используя соотношение (5.18), получаем" к Гс (Л = о (Л I + I 7,U )Dri (/)D t (./) .(520) с 1 i = i Таким способом фоновый шум становится пространственно "выбеленным", а собственные значения и собственные векторы преобразованной МВСП (5.20) обладают указанными ранее теоретическими свойствами. Конечно, для определения координат источника сигнала будет необходимо использовать преобразованный вектор источника сигнала D,(/,6) = C(/)D(/,e).(5.21) Кроме того, можно показать, что нет необходимости точно знать о пространственной когерентности фонового шума. Достаточно, чтобы она согласовывалась с общей структурой или моделью, в которой несколько параметров могут оставаться неизвестными. Такая модель МВСП записывается в виде J (J, m), где m - вектор неизвестных параметров. Пусть С (/, т) является матрицей, такой, что C(/,m)J(/,m)C+(/,m)=I,(5.22) а m0 - истинное значение вектора параметров фонового шума. Выражение для преобразованной с помощью матрицы C(f, m) МВСП будет иметь вид Гс(/,т)=С(/,т)Г(/)С+(/,т),(5.23) и, следовательно, Гс (f, m) = a (/) С (/, m) J (/, m) C+ (f, m) + + I 7;(0C(J,m)D,.(/)Dr(y)C+(/,m).(5.24) Очевидно, что если вектор m изменяется и принимает различные значения, то при достижении ими значения т0 фоновый шум становится абсолютно некогерентным. Следовательно, если собственные значения матрицы Гс(/, т) представить в виде графиков в зависимости от m, то N-K наименьших собственных значений станут равными при m=m0. Действуя таким образом, возможно найти значение т0 и пространственно "выбелить" фоновый шум среды. Конечно, на практике имеется лишь оценка f (f) матрицы T(f) и, когда собственные значения f с (/, m) = С {f, m) f (J) C+ (/, m)(5.25) представляются в виде графика в зависимости от т, вместо идеального выбеливания можно наблюдать сходимость наименьших собственных значений к общему пределу. Эта сходимость проявляется в большей степени по мере увеличения времени наблюдения. Значение m в точке сходимости одновременно дает: 1) оценку т0 параметра т0 шума и 2) число источников сигналов. Подпространство сигналов и ортогональное ему подпространство определяются собственными векторами оценки МВСП, полученной в результате преобразования с использованием C(f, m0). Таким путем получается оценка МВСП сигналов гю
Г If) P- 80 0,5J S) m о 0,5 1 B) m Рис. 5.4. Зависимости собственных значенийшума и сигналов двух источников от параметра к ге„ т при в> =()0>- я> 1 (/) ; б) Г (/) при/> = 80; в)Г(/) приР = 400 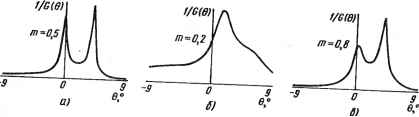 Рис. 5.5. Диаграммы G"1 (6) для шумового поля, характеризуемого зависимостями на рис. 5.4 (метод ортогонального подпространства) С" U rh0) X 1Л-(Я - W)J*i{f)V 1/)}[С +(/, *о)] 1,(5.26) где Л/ - оценка числа источников сигналов; \Jf) - TV наибольших собственных значений матрицы Tc(f, m0); V,-(/) - N собственных векторов, соответствующих N наибольшим собственным значениям матрицы TC(J, m0); о if) - среднее значение К-N наименьших собственных значений. Для проверки возможностей метода было проведено моделирований на очень простом примере описанной ранее антенной решетки. Модель про- странственной когерентности фонового шума характеризовалась соотношением (5.16) и соответствовала модели шума водной поверхности. Это модель с одним неизвестным параметром т. Поле сигналов создается двумя источниками с углами визирования 0 и 4° ; ОСШ = -10 дБ; параметр пространственной когерентности шума те =0,5. На рис. 5.4 представлены три вида1 зависимостей собственных значений от параметра т: а) полученных теоретически; б, в) при использовании оценки МВСП согласно (5.14). Нетрудно видеть, что для теоретической МВСП при ш = 0,5 минимальные собственные значения одинаковы, а два наибольших собственных значения соответствуют сигналам источников. При использовании оценки точка сходимости минимальных собственных значений наблюдается при значении параметра т=0,5. Причем качество сходимости улучшается с увели-96 чением времени наблюдения Р. На всех рис. 5.4 ясно видны графики двух собственных значений, соответствующих источникам сигналов, которые располагаются выше графиков "шумовых" собственных значений. Результаты расчетов по методу ортогонального подпространства (как и ранее, приводятся значения функции G1 (в)) даны на рис. 5.5. Наилучшие результаты получаются, конечно, при т = 0,5. Таким образом, благодаря параметрическому моделированию пространственной когерентности фонового шума области применения метода ВРС значительно расширились и стали адекватны действительным условиям работы антенной решетки. Следующий подраздел посвящен анализу предположений относительно параметров волновых фронтов самих сигналов при использовании метода ВРС, когда параметры D(f, В) оказываются неизвестными. 5.3.2. Использование подпространства сигналов [з] Матрица взаимных спектральных плотностей сигналов, как это следует из (5.26), является вырожденной (с нулевыми собственными значениями), однако, конечно, неотрицательно-определенной. Ранг этой матрицы равен числу источников сигналов, а векторы источников полагаются линейно независимыми. В действительности эта матрица является суммой МВСП отдельных источников. Матрица взаимных спектральных плотностей каждого источника является диадным произведением соответствующего вектора источника сигнала на себя. Поэтому проблема состоит в том, чтобы узнать, можно ли получить векторы источников сигналов, имея МВСП источников. Необходимость обращения к модели сигналов. Следует отметить, что антенная решетка как таковая в лучшем случае позволяет определить только векторы отдельных источников. Для того чтобы, зная параметры волнового фронта, перейти к определению положения источника сигнала в среде распространения, потребуется дополнительная информация о передаточных функциях среды от источника до элементов антенной решетки. Другими словами, необходимо иметь модель среды распространения для описания волнового фронта как функции координат источника сигнала. Если форма волнового фронта уже получена на основании МВСП источников сигналов, то потребуется найти координаты и спектр источника путем идентификации параметров измеренного фронта волны с соответствующими параметрами волнового фронта, заданного моделью. Невозможно определить положение источников без модели среды. Однако даже перед этим этапом локализации необходимо знать: не потребует ли первая задача описания волновых фронтов на основе МВСП дополнительной информации о параметрах волновых фронтов, а следовательно, и о среде распространения? Иначе говори, можно ли вычислить векторы неизвестных источников сигналов только на основе МВСП? Точный ответ на этот вопрос: нет, нельзя. Тем не менее на основе МВСП можно найти векторы источников сигналов только в виде функций от ряда неизвестных скалярных параметров. Число таких параметров равно K(K-\)j2, и можно сказать, что для полного определения параметров волновых фронтов не хватает только произвольной унитарной матрицы порядка К. Для определения этой матрицы необходимы некоторые априорные знания или предположения о характере волнового фронта или о сложности среды распространения, иными словами, необходима некоторая модель. Одноэтапная процедура вычисления координат источника сигнала. Один из возможных подходов сводится к решению задачи определения векторов источников сигналов и их координат с помощью одноэтапной процедуры. С одной стороны, имеется выражение для векторов источников, полученное на основе экспериментальной МВСП, но только как функции К(К-\)12 неизвестных скалярных параметров. С другой стороны, строится модель, которая дает другое выражение для векторов источников сигналов, где неизвестными параметрами оказываются: К значений спектральной плотности; ЗК координат источников сигналов; "свободные" скалярные величины, которые используются для описания среды распространения в рамках априорной структуры, но без указания численных значений параметров. Эти параметры являются одинаковыми для всех источников сигналов, и их общее число полагается равным /- Поэтому для идентификации выражений К векторов источников сигналов (каждый из них содержит N составляющих) имеется: (4K+Z) неизвестных скалярных величин "модели"; К(К- 1)/2 неизвестных скалярных величин МВСП. Поскольку число возможных скалярных уравнений равно KN, то в результате идентификации можно получить значения всех неизвестных скалярных величин, если KN=4K+Z+ [К (К-1)12].(5.27) Таким образом число параметров, "характеризующих среду распространения" Z в рамках выбранной модели, не может быть больше Z = K[N-(K+7)/2].(5.28) Это число растет с увеличением числа элементов антенной решетки N. Иными словами, число элементов решетки N согласно (5.28) определяет число параметров Z, характеризующих среду распространения. Чем больше Z, тем сложнее среда. Нетрудно видеть, что число параметров Z возрастает также с увеличением числа источников сигналов К, которых, как предполагается, значительно меньше N. Поэтому среда распространения поддается более полному описанию, когда число элементов решетки и число источников сигналов велико. Например, для 50-элементной антенной решетки и 11 источников сигналов получается Z=410, а при 21 источнике число параметров Z = 720. Однако эти значения могут рассматриваться только как приблизительные, так как должен выполняться ряд других условий. Например, координаты должны быть действительными числами (заметим, что рассматриваемые ранее KN уравнений являются комплексными). 98 Двухэтапная процедура вычисления координат источников сигналов. Другой возможный подход к решению этой задачи основывается на том, что количество априорной информации для описания только векторов источников сигналов оказывается намного меньше количества информации, требуемой для построения модели среды распространения. Например, можно согласиться с тем, что без существенных упрощений любой вектор источника сигнала может быть представлен в виде когерентной суммы плоских и (или) сферических волн. Поэтому, прежде чем делать какие-либо предположения относительно модели среды распространения, можно определить общую структуру векторов источников сигналов. Общее число свободных параметров должно соответствовать системе из KN уравнений с К (К-1)/2 неизвестными параметрами. Следовательно, это общее число параметров составляет KN- [К (К - 1)/2] =К [N-K(K - 1)/2].(5.29) Таким образом, для каждого вектора источника сигнала в принципе должно быть N- (К - 1)/2 свободных параметров для их представления суммой плоских и (или) сферических волн. Используя априорную информацию относительно сложности А волновых фронтов, одним из них можно поставить в соответствие больше элементарных волн, чем другим. Таким образом, как и при одноэтапной процедуре, в конце осуществляется идентификация с использованием численных выражений для всех векторов источников сигналов, требующих лишь минимума априорных сведений. При этом каждый вектор источника моделируется как сумма векторов элементарных волновых фронтов. Затем, на втором этапе вычислений, необходимо использовать модель среды распространения, которая, конечно, должна быть совместима со всеми ранее рассчитанными векторами источников сигналов. Поскольку на каждый источник сигнала (как и при одноэтапной процедуре) приходится четыре скалярных параметра, число параметров Z, характеризующих среду распространения, будет определяться выражением KN=4K + Z.(5.30) Необходимо отметить, что Z оказывается немного больше Z при одноэтапной процедуре, поскольку из-за наложения ограничений (даже незначительных) на общую форму волновых фронтов образуется большее "множество свободных" параметров для среды распространения. Очевидно, что аналогичный подход используется в задаче описания среды с известными источниками сигналов (по координатам и спектральной плотности) . Такие источники не требуют параметров вообще, и свободных параметров для описания среды распространения оказывается больше. 5.3.3. Использование метода ортогонального подпространства Для получения модели волновых фронтов методом ортогонального подпространства можно (как это делалось и ранее) использовать параметры среды распространения. Тогда модель вектора источника сигнала будет 0 ... 12 13 14 15 16 17 18 ... 78 |












