Раздел: Документация
0 ... 9 10 11 12 13 14 15 ... 78 осуществляется итеративное вычитание составляющей из диагональных элементов матрицы R до тех пор, пока результирующая матрица не станет сингулярной. Полученная таким образом сингулярная матрица используется в качестве оценки матрицы Р, затем определяется ее ранг и выполняется разложение Холецкого. В действительности оценка R, полученная при конечном времени усреднения, не будет содержать собственные значения Ад. = = сг2 при К+ 1 <k<JV, как в модели (4.12). Подобная ошибка моделирования приведет к преждевременному окончанию упомянутого процесса. Результатом являются более слабое подчеркивание основных мод и значительная вычислительная сложность из-за большой размерности задачи разложения (число столбцов в матрице С слишком велико, а составляющие сигнала недостаточно разнесены). Последний вариант метода прямого вычисления сводится к оценке ортогонального дополнения {Мд :k=K~+l, К+2,... ,N] к основным модам {М/с: k = 1,2,... ,К} . Эта оценка основывается на соотношении XMtMi = IN=(4.49 а) k= 1 = Ьм* + 4 I M*Mi(449б) или £мкМк = 1„- £ МкМк.(4-5°) к = 1к = А + 1 При подчеркивании основных мод подстановка (4.11 б) в (4.50) дает ще= со)"1 =-2{lN~ 1М,мЛ=~ £ MkMk(4.51) и модифицированные оценки по критериям МД и МЭ могут быть описаны выражениями [16-18,28] ммД т = iv °2->(4-52> X Ю(в)мкр к = к+1 £ ii;mj2 РММЭ(Й) = ,- .(4.53) к=к+ 1 Приведем интуитивное объяснение соотношений (4.52) и (4.53). Векторы Mfc, входящие в них, располагаются в векторном подпространстве, ортогональном подпространству, порожденному основными модами. Поэтому, когда вектор D(9) располагается в подпространстве сигнала, выполняется соотношение MD(8) =0 при К+ 1 <fc<7V и значения функций, определяемые (4.52) и (4.53), могут стать (по крайней мере, теоретически) бесконеч-76 ними. Очевидно, что таких бесконечных значений не может быть из-за невозможности точной оценки основных мод или их ортогональных дополнений при конечном времени усреднения. Этот вопрос рассматривается более полно в разд. 4.6. 4.6. ОЦЕНИВАНИЕ ДАЛЬНОСТИ С ВЫСОКОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТЬЮ При пассивном методе обнаружения источника сигнала с использованием линейной антенной решетки возникает задача оценки двумерного спектра мощности (по дальности и углу визирования), получаемого в результате обработки выборки выходных сигналов решетки объема Т. Здесь рассматриваются три спектральные оценки: 1) на основе преобразования с равномерным взвешиванием и усреднением, названным здесь фокусировкой луча (ФЛ) [29, 30]; 2) по методу МД; 3) по методу МЭ [10]. Вектор антенной решетки, формирующий сфокусированный на источник сигнала луч, 1)(В) = = 1)(г ) при известных частоте / и угле визирования /3 определяется соотношением (4.66). На рис. 4.3 показана схема такого преобразующего устройства. Устройства оценки по критериям МД иМЭ отличаются только операциями над оценкой корреляционной матрицы R. Основное внимание в этом разделе уделено определению спектральной оценки дальности с учетом того, что аналогичные характеристики эффективности можно получить и для случая измерения угловой координаты. Спектральные оценки дальности методами ФЛ, МД и МЭ анализируются в сравнении с их модифицированными вариантами, в которых используется разложение на основные моды (МФЛ, ММД и ММЭ). При этом наибольший интерес представляют результаты сравнения средней квадратической ошибки оценки дальности с ее нижней границей при наличии как одного, так и двух источников сигнала. Для одиночного гауссовского сигнала на фоне пространственно некоррелированного изотропного гауссовского шума с нулевым средним значе- Многоканальный коррелятор
Рис. 4.3. Схема устройства с фокусировкой луча для оценки дальности г0 источника сигнала JSJamaa граница Крамера-Рас для дисперсии 1 --г- I V ~2 л! -7. \ I (4.54) ™« дается формулой [31]- е Л/ - imrnn 1 J где Л, - число элементов антенной решетки- А °>2 - «сношение сигнал-шум (ОСшГкГв™ ~ ДПИНа ВОЛНЫ си™ала; шехки; Г-число выборок на инйгх.а"ГС>"°Й U"2 + х„2 - 2 «„г cos /?)"2 (4.55) а = - У г, (4.56) В качестве простого примера для моделирования линейной антенной решетки были выбраны следующие параметры: г =4000Х; /3 = 90°; УУ=3. Рассматривалась эквидистантная решетка с межэлементным расстоянием d = 75 А. Зависимости средней квадратической ошибки оценки дальности от ОСШ при выбранных параметрах для различных спектральных оценок дальности представлены на рис. 4.4. Необходимо отметить, что действительная эффективность выше эффективности, характеризуемой нижней границей. Это обусловлено двумя причинами. Во-первых, как для получения результата (4.54), Фл ммд мд ммэ МЭ Оценка Крамера-Рао -------5Щ(дг/12)  Т=400 Рис. 4.4. Зависимость средней квадратической он™*™ для различных устройств спектральной оценки°ЦеНКИ дальнос™ °т ОСШ 78 так и для построения устройств обработки применялась модель комплексного гауссовского сигнала (т.е. с некогерентной огибающей), тогда как при моделировании использовался когерентный сигнал фиксированной частоты. Во-вторых, выбиралась схема оценки со строб-импульсами дальности. Из этого следует, что результаты моделирования будут согласовываться с ожидаемыми значениями нижней границы либо при большом ОСШ, либо при значительном времени усреднения Т. При малых ОСШ и непродолжительном времени усреднения дисперсия оценки дальности стабилизируется. Этот эффект объясняется тем, что строб-импульсы дальности располагаются на участке, где возможно появление пика в спектре, так, чтобы исключались аномальные ошибки при высоком ОСШ и большой длительности Т. При длительности строб-импульса, равной q, низком ОСШ или малой продолжительности Т гистограмма оценки становится практически постоянной, а результирующее значение дисперсии оценки приближается к q2/12. В [32] рассматривается аналогичная проблема, когда строб-импульсы дальности служат для предотвращения выбора боковых лепестков в функции взаимной корреляции. Использование строб-импуяьса дальности в данном случае обусловлено тем, что расположение истинного пика в функции отклика инвариантно к X. Из этого следует, что на основе зависимости отклика от частоты можно произвести разрешение побочных пиков в спектре. Наиболее важный вывод из результатов моделирования, представленных на рис. 4.4, состоит в том, что каждое устройство оценки с высокой разрешающей способностью обеспечивает такую же среднюю квадратическую ошибку, как и система с фокусировкой луча. Исключение составляет устройство обработки, обеспечивающее максимум энтропии. Устройства МЭ и ММЭ оценки при высоком ОСШ имеют меньшую эффективность, приближающуюся к эффективности при гауссовском сигнале, хотя фактически присутствует когерентный сигнал. По мере уменьшения ОСШ эффективность МЭ оценки приближается к эффективности оценок ФЛ и МД. Это согласуется с предположением об относительной эффективности МЭ оценки [33]. Для оценки способности разрешения двух пиков в спектре мощности, обусловленных сигналами, используются две метрики: ширина пика 5 отклика от одного источника на уровне 3 дБ от максимального значения, как показано на рис. 4.5, и средняя квадратическая ошибка измерения дальности одного источника сигнала в присутствии другого. В табл. 4.1 приведены значения ширины пика в спектре мощности по уровню 3 дБ для различных рассматриваемых методов. Эффективный коэффициент модификации е для оценки дальности является функцией ОСШ и времени наблюдения Т. На рис. 4.6 представлены зависимости ширины основного пика от ОСШ для рассмотренных ситуаций. Для сравнения на рис. 4.6,а показаны теоретические данные для МД и МЭ оценок, свидетельствующие о хорошем совпадении теории и эксперимента при высоком ОСШ (> - 3 дБ) и большом времени усреднения (7П>25). Возможности повышения разрешающей способности при использовании модифицированных оценок ММД и ММЭ, как убедительно показано на рис. 4.6, зависят как от времени усреднения, так и от ОСШ. В табл. 4.2 пред- 79 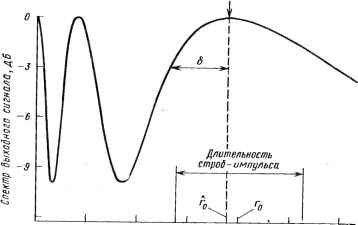 100175250325ШЬ75550 Дальность (в длинах долн) х!0 Рис. 4.5. Типичная форма спектра на выходе устройства оценки методом ФЛ. Дальность источника сигнала гв =4000А., диапазон дальности (3000-50001X ставлены эмпирически найденные значения коэффициента модификации для оценок МД и МЭ в зависимости от этих двух параметров. Из данных табл. 4.2 видно, что разрешающая способность увеличивается с ростом Т. Более того, данные говорят о том, что потенциальные возможности оценки МД выше, чем оценки МЭ. Однако абсолютные значения ширины пика по уровню 3 дБ для оценок МЭ и ММЭ оказываются еще несколько меньше, чем для оценок МД и ММД соответственно. Наблюдаются несколько меньшие значения средней квадратической ошибки при оценках МД,и ММД, Таблица 4.2. Коэффициент модификации для оценок МД и МЭ {г =2000 X)
Рис. 4.6. Зависимости ширины пика fi в спектре мощности, измеренные на уровне 3 дБ, от ОСШ: а) Г = 400; б)Т = 25-> 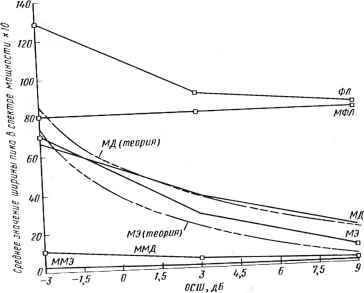 п) 1>t0 I 120 - Со 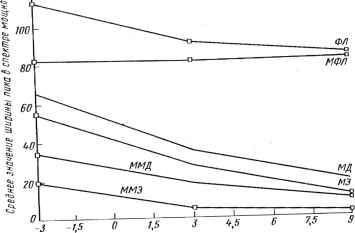 ОСШ, ДБ В) 0 ... 9 10 11 12 13 14 15 ... 78 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












