Раздел: Документация

0 ... 10 11 12 13 14 15 16 ... 78

чем при соответствующих оценках МЭ. Наконец, важно отметить, что оба типа модифицированных оценок позволяют обеспечить очень высокую разрешающую способность при достаточно большом времени усреднения. Это справедливо даже для уровней ОСШ < -3 дБ.

Для анализа эффективности оценки дальности при наличии двух источников сигнала обозначим их дальности как г, и г2. Будем считать, что х(г) является /V-мерным вектором антенной решетки при числе источников J = 2. Предположим, что сигналы источников и шум не коррелированы. Ковариационная матрица вектора сигнала х(У) определяется выражением R = Е[х(/)х(*)] =(4.57)

= аЦаЩгЩг,) + (1 - a)D(r,)D(r2)] + гг% ,(4.58)

где 0<a< 1 характеризует относительную мощность источников сигналов. Поскольку сигнал x(t) полагается комплексным, гауссовским с нулевым средним значением, плотность вероятности х(/) имеет "вид

F(x(/)/r,, г2) = пйТоТ ехр t x(fVR х(/)]-(459)

Л К

Нижняя граница дисперсии для несмещенной оценки вектора дальности г определяется cov(r ) = J ~l (г ), где J (г ) - информационная матрица Фишера размера 2X2. Элемент Ц матрицы J (г ) определяется выражением

[J(r)]0= -К

РЦх/г) cV, Prj

где

Цх/г) = - MN log л - N log j RI - X "()R x(z).

Используя равенство

( I >R

dr, cr.

(4.60)

(4.61)

(4.62)

можно получить соотношения для 7n , J 22 и Jl2, являющиеся функциями фокусирующих векторов, ОСШ, числа элементов антенной решетки и объема выборки. Для большого ОСШ и Хп <Сг;- (/ = 1,2) [3,34]

(1 ~ о.)Мо2с

N

2N

1п\~ аа.

NX,2, - Х„

I +

(1 -Ы2)

DV

(4.63)

./,, - 2N

i +-r4i -Ы2)

а

DV

(4.64)

где

г, - Х„ cos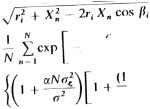

и= 1,2,..., N; i= U2,

/2тс j (ти - т

2„)];

(4.65) (4.66) (4-67)

Остальные составляющие определяются нижней границей дисперсии при одиночном источнике сигнала. Нижними границами дисперсии оценки Г] и г2 являются J~[\ и J и соответственно. Эти выражения позволяют понять характер изменения эффективности при оценке дальности нескольких источников сигналов. Например, если £=0, то нижние границы дисперсии для Г и г2 оказываются такими же, как в случае одиночного источника сигнала, и определяются выражением (4.54). Если g ф 0, то можно показать, что нижние границы дисперсии для гх и г2 будут больше. На самом деле, JTt и./и являются монотонно возрастающими функциями \g\.

В качестве иллюстрации эффективности методов с высокой разрешающей способностью при оценке дальности двух источников сигналов на рис. 4.7 показано типичное семейство спектральных характеристик, полученное при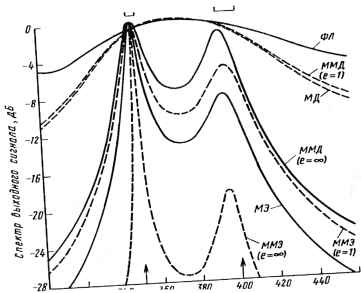

ЗОВ

ПО 3W 360 380 Ш Дальность (В длинах Волн) *Ю

„Rvx источников сигналов, дальности ко-

83

---

моделировании. При моделировании полагалось, что ОСЫ =9 дБ; 7=100; Л/=5; d = 15X; гх =3500л и r2=4000X. В верхней части рисунка для обоих источников сигнала показаны интервалы среднего квадратического отклонения в оценке дальности, центрированные относительно истинного значения дальности каждого из источников. Как видно из рис. 4.7, форма выходных сигналов показывает возможность разрешения двух источников сигналов, за исключением случая е = 1 для оценок ФЛ, МД и ММД. При модифицированных оценках используются две основные моды (К= 2), для которых оцениваются собственные значения и собственные векторы. Уровень отклика на дальности гг =4000Х ниже, чем на гх =3500Х, так как на дальности гг сказывается влияние уменьшения разрешающей способности, в результате чего точечный источник ведет себя как протяженный с той же мощностью. Очевидно, что модифицированные оценки при е=°° демонстрируют высокую разрешающую способность. Невозможность разрешения двух источников сигналов с помощью оценок ФЛ, МД и ММД при е-1 обусловливается критическим значением ошибки смещения от 200 до 300Х и полностью искаженным видом спектра.

4.7. ЗАКЛЮЧЕНИЕ

Представлены две процедуры спектрального анализа с высокой разрешающей способностью, основанные на использовании широко известных критериев минимума дисперсии и максимума энтропии. Эти процедуры демонстрируют более высокую и ограничиваемую только временем наблюдения разрешающую способность, чем процедуры оценки МД и МЭ. Наличие только такого ограничения должно существенно повлиять на применение метода спектрального анализа в тех случаях, когда основную роль играет ошибка смещения, а не случайные флуктуации оценки.

СПИСОК ЛИТЕРАТУРЫ

[1] R. Т. Lacoss, "Data Adaptive Spectrum Analysis Methods," Geophysics, J6(4):661-675 (Aug. 1971).

[2] J. Capon, "High-Resolution Frequency-Wavenumber Spectrum Analysis," Proc. IEEE, 57: 1408-1418(1969).

[3] N. L. Owsley and G. Swope, "High Resolution Range Estimation with a Linear Array," Proc. IEEE EASCON 82, Washington, DC, Sept. 1982.

[4] N. L. Owsley, "An Overview of Optimum Adaptive Control in Sonar Array Processing," in K. S. Narendra and R. V. Monopoli, eds., Applications of Adaptive Control, Academic Press, New York, 1980, pp. 131-164.

[5] J. P. Burg, "Maximum Entropy Spectrum Analysis," 37th Annu. Meet. Soc. Explor.

Geophys., Oklahoma City, Okla, 1967. [6] J. P. Burg, "The Relationship between Maximum Entropy and Maximum Likelihood

Spectra," Geophysics, 37(2) .375-376 (Apr. 1972) [TJ A. Vanden Bos, "Alternative Interpretation of Maximum Entropy Spectral Analysis,"

IEEE Trans. Inf. Theory (Corresp.), i Г-У7:493-494(July 1971).

[8] N. L. Owsley, "Adaptive Data Orthogonalization," Proc. IEEE ICASSP, Tulsa, Okla., Apr. 1978, pp. 109-112

84

[9] N. L. Owsley, "Modal Decomposition of Data Adaptive Spectral Estimates," Yale Y Univ. Workshop Appl. Adaptive Syst. Theory, K. S. Narendra, ed., May 1981. [10] N. L. Owsley and J. F. Law, "Dominant Mode Power Spectrum Estimation," Proc.

IEEE ICASSP, Paris, Apr. 1982. [11] D. Tufts and R. Kumaresen, "Data-Adaptive Principal Component Signal Processing,"

Proc. 1980 IEEE CDC, Albuquerque, N.M., Dec. 1980. -ь

[12] L. J. Griffiths, "A Continuously Adaptive Filter Implemented as a Lattice Structure," I Proc. IEEE ICASSP, Hartford, Conn, 1977.

[13] W. S. Liggett, "Passive Sonar: Fitting Models to Multiple Time Series," in J. W. R.

Griffiths et al, eds. Signal Processing, Academic Press, 1973. [14] N. L. Owsley, "A Recent Trend in Adaptive Spatial Processing for Sensor Arrays:

Constrained Adaptation," in J. W. R. Griffiths, et al, eds. Signal Processing, Academic

Press, New York, 1973.

[15] H. Mermoz, "Complementarity of Propagation Model Design with Array Processing," in G. Tacconi, ed. Aspects of Signal Processing, D. Reidel, Dordrecht, The Netherlands, 1977.

[16] A. Cantoni and L. Godara, "Resolving the Directions of Sources in a Correlated Signal Field Incident on an Array," J. Acoust. Soc. Am., 67(4):1247-1255 (Apr. 1980).

[17] G. Bienvenu and L. Koop, "Adaptive High Resolution Spatial Discrimination of Passive Sources," in L. Bjorno, ed. Underwater Acoustics and Signal Processing, D. Reidel, Dordrecht, The Netherlands, 1981.

[18] R. Klemm, "High-Resolution Analysis of Nonstationary Data Ensembles," Signal Processing: Theories and Applications, Elsevier-North Holland Publishing Co, Oct. 1980, pp. 711-714.

[19] International Mathematical and Statistical Libraries Inc., Eigensystem Analysis, 9th ed.

Vol. 2, IMSL, Houston, 1982, Chap. E. [20] D. Tufts and R. Kumarasen, "Singular Value Decomposition and Spectral Analysis,"

Proc. IEEE ASSP Workshop Spectral Anal., McMaster University, Hamilton, Ont,

Aug. 1981.

[21] D. Johnson, "Improving the Resolution of Bearing in Passive Sonar Arrays by Eigenvalue Analysis," Proc. First ASSP Workshop Spectral Anal., McMaster University, Hamilton, Ont, Aug. 1981.

[22] W. Gabriel, "Adaptive Superresolution of Coherent RF Spatial Sources," Proc. First ASSP Workshop Spectral Anal., McMaster University, Hamilton, Ont, Aug. 1981.

[23] S. Pasupathy and A. N. Venetsanopoulos, "Optimum Active Array Processing Structure and Space-Time Factorability," IEEE Trans. Aerosp. Electron. Syst, AES-ЩбуЛО-778 (Nov. 1974).

[24] Special Issue on Time Delay Estimation, Part II, Trans. IEEE Acoust. Speech Signal Process., ASSP-29[3) (June 1981).

[25] L. Ng and Y. BarShalom, "Time Delay Estimation in a Multitarget Environment," Proc. 21st IEEE CDC, Orlando, Fla, Dec. 1982.

[26] О. B, Gammelsaeter, "Adaptive Beamforming with Emphasis on Narrowband Implementation," in L. Bjorno, ed. Underwater Acoustic and Signal Processing, NATO ASI Series C, D. Reidel, Dordrecht, The Netherlands, 1981, pp. 307-326.

[27] N. L. Owsley, "Adaptive Data OrthogonaUzation," Proc. IEEE ICASSP, Tulsa, Okla, Apr. 1978, pp. 109-112.

85

---

[28] R. Schmidt, "Multiple Emitter Location and Signal Parameter Estimation," Proc.

RADC Spectral Estimation Workshop, Rome, N.Y., 1979. [29] G. C. Carter, "Time Delay Estimation for Passive Sonar Signal Processing," IEEE

Trans. Acoust. Speech Signal Process., ASSP-29(3):463-470 (June 1981). [30] N. L. Owsley and G. R. Swope, "Time Delay Estimation in a Sensor Array," IEEE

Trans. Acoust. Speech Signal Process >4SSP-29(3):519-523 (June 1981). [31] W. J. Bangs and P. Schultheiss, "Space-Time Processing for Optimal Parameter Estimation," in J. W. R. Griffiths et al., eds., Signal Processing, Academic Press, New York, 1973, pp. 591-604.

[32] J. P. lanniello, "Threshold Effects in Time Delay Estimation Using Narrowband Signals," IEEE ICASSP 1982, Paris, May 3,1982, pp. 375-379.

[33] A. B. Bagger oer, "Confidence Intervals for Maximum Entropy Spectral Estimates," in Aspects of Signal Processing, Part I, NATO Advanced Study Institute, D. Reidel, The Netherlands, 1976.

[34] G. Swope, Ph.D. thesis, Rensselaer Polytechnic Institute, Aug. 1982. 5

ПРИНЦИПЫ ОБРАБОТКИ СИГНАЛОВ АНТЕННЫХ РЕШЕТОК, ОБЕСПЕЧИВАЮЩИЕ ВЫСОКУЮ РАЗРЕШАЮЩУЮ СПОСОБНОСТЬ

Г. Бьенвеню1, А. Мермо2 5.1. ВВЕДЕНИЕ

Одной из главных функций подводных пассивных приемных систем является определение числа источников сигналов, а также параметров этих источников. Основным способом при этом является пространственная обработка сигналов, позволяющая производить разрешение источников излучения, используя их пространственные характеристики. Традиционный метод анализа сигналов в системах с антенными решетками реализуется на базе диаграммообразующей схемы; с целью повышения эффективности устройств этого типа были созданы адаптивные диаграммообразующие схемы. Этот метод обеспечивает увеличение КНД антенной решетки, которьш асимптотически ограничивается лишь отношением сигнал-шум на выходе антенного датчика. Недавно появились более эффективные методы, получившие название методов с высоким разрешением. Увеличение эффективности этих методов но сравнению с предшествующими методами обработки основано на учете дополнительных предположений относительно среды распространения. Тем не менее эти методы позволяют вводить свободные параметры для модели среды распространения, что увеличивает их гибкость.

Теория адаптивной обработки сигналов антенных решеток как классическая теория построения диаграммообразующих схем базируется только

1Фирма Thomson-CSF, Кань-сюр-Мер, Франция.

2Фирма Telecommunications, Си-Фур-ле-пляж, Франция.

на информации об источниках излучения и условиях распространения излученных сигналов. При этом источники сигналов полагаются точечными. Сигналы от таких источников, пройдя через антенную решетку, сохраняют идеальную пространственную когерентность. В общем случае форма волнового фронта (после его преобразования элементами решетки) является известной функцией координат (угловых и дальности) источника сигнала. Предполагается, что передаточная функция антенного элемента также полностью известна. Это последнее условие характеризуется вектором источника сигнала D(f). Пусть вектор г (г) является вектором, представляющим совокупность сигналов, принятых N антенными элементами. Этот вектор будет характеризоваться также матрицей-столбцом

r+(f) = [r,(f), ...,r„(f), ...,rN(i)],(5.1)

где г + (г) - транспонированный и комплексно-сопряженный вектор; rn(t) - сигнал, принятый п-м элементом решетки. Корреляционная матрица принятого сигнала определяется выражением

C(T) = £[r(f)r+(t + T)],(5.2)

где Е() - математическое ожидание. Матрица взаимных спектральных плотностей (МВСП) принятого сигнала обозначается через Г(/). Известно, что Г(/) является преобразованием Фурье матрицы С (г). С учетом сделанных замечаний МВСП для одиночного источника обладает вполне определенными свойствами, которые можно выразить следующим соотношением:

T(/) = y(/)D(/)D+(/),(5.3)

где D(/) - вектор, определяемый передаточными функциями каждого элемента антенной решетки для сигнала источника. Эта совокупность передаточных функций нормируется так, чтобы значение квадрата модуля вектора D(/) было равно N; y(f) является спектральной плотностью сигнала, рринятого от источника. Вектор D(/) характеризует форму волнового фронта и может быть вычислен, если априорно задано угловое положение в источника сигнала. Ранг матрицы T(f) равен единице, что соответствует полной пространственной когерентности. Последнее предположение состоит в том, что источники сигналов взаимно не коррелированы и не кор-релированы с шумовым фоном.

С учетом сделанных замечаний общая МВСП выходных сигналов элементов антенной решетки может быть записана в виде

Г (О = Гш (0 + £ у, (/)D,. (/)D + (Л ,(5.4)

i = 1

где Гш (/) - МВСП шума; К - число элементов антенной решетки.

Методы, обеспечивающие высокую разрешающую способность (ВРС), требуют для своей реализации ряда предположений, касающихся характеристик среды распространения. В частности, всегда имеется некоторая информация о пространственной когерентности фонового шума. В резуль-

87

0 ... 10 11 12 13 14 15 16 ... 78