Раздел: Документация
0 1 2 3 4 ... 78 образом на вычислении минимальных собственных значений и соответствующих им собственных векторов. Проблема собственных значений интенсивно изучалась многими теоретиками начиная с 1947 г., когда собственные значения стали рассчитывать с помощью настольных калькуляторов. В гл. 6, которой завершается часть I, делается несколько убедительных замечаний по многим аспектам этой проблемы, включая вопрос о том, как эффективные параллельные вычисления будут использованы для получения полезной информации о собственных и сингулярных значениях. Т. Кайлат 1 ОБРАБОТКА СИГНАЛОВ В ЭПОХУ СБИС Т. Кайлат1 1.1. ВВЕДЕНИЕ Предложенное Кули и Тьюки почти два десятилетия назад быстрое преобразование Фурье (БПФ) в сочетании с накопленным к тому времени опытом в технологии цифровых систем привело к революции в обработке сигналов. Наряду с прочим эта революция характеризуется развитием нового направления, которое получило название цифровой фильтрации или цифровой обработки сигналов (см., например, хорошо известную книгу Оппенгейма и Шафера2). Около десяти лет назад пионерской работой Ахала и его сотрудников из фирмы Bell Laboratory, а также Итакурой и Саито в Японии идеи временной обработки были вновь применены к анализу и синтезу речи (см., например, [45]). В сочетании с развитием "технологии интегральных схем это направление возвещает об еще одной революции в обработке сигналов, о чем свидетельствует, например, появление кристалла Speak-and-Spell фирмы Texas Instruments и возрастающий интерес к параллельным алгоритмам и архитектурам (см., например, специальный выпуск журнала IEEE Computer Magazine за январь 1982 г., посвященный быстрым параллельным вычислениям) . Основной особенностью нового направления является акцент на формулировку оптимизационных критериев в задачах обработки сигналов. Цель состоит в том, чтобы, не связываясь преждевременно с конкретным способом реализации, создать математическую модель с определенным критерием эффективности, удовлетворение которому будет определять последовательность операций обработки сигналов. Конечно, всегда имеются ограниче- Станфордский университет, Станфорд, Калифорния. 2 Оппенгейм Л. В., Шафер Р. В. Цифровая обработка сигналов: Пер. с англ. - М.: Радио и связь, 1 979. ния при создании реалистичных, но не очень сложных математических моделей и подходящих критериев оптимизации. Однако подобные проблемы уже встречались и были удачно преодолены в статистической теории связи, управления и идентификации. Специфические особенности задач обработки сигналов часто делают желательным применение процедуры линеаризации, поэтому значительная часть теории и практики современной обработки сигналов в конечном счете связана с решением систем линейных уравнений. На первый взгляд зто разочаровывает, поскольку подобные вопросы изучаются в течение настолько длительного времени, что сказать что-то новое о них, кажется, уже нельзя. Но дело в том, что для наиболее интересных физических задач непосредственное численное решение уравнений не представляет большой ценности; весь интерес заключается в специальной структуре уравнений и методах согласования с ней современных аппаратурных средств, позволяющих сокращать время нахождения решений и уменьшать сложность реализации. Так БПФ и структуры матричных процессоров оказали решающее влияние на традиционные представления о том, как находить эмпирические спектральные оценки. Аналогично этому модели с пространством состояний в теории управления привели в 60-х гг. к революции в возможностях обработки больших массивов данных вследствие осознания того факта, что для обработки достаточно отслеживать изменения фиксированного конечномерного марковского вектора состояний. В настоящее время относительная доступность устройств памяти делает менее необходимым концентрацию предыдущей информации в фиксированном конечномерном векторе состояний; теперь часто проще наращивать память, приводя в соответствие ее емкость с объемом данных. Проиллюстрируем это в данной главе. Появление однокристальных арифметических устройств с плавающей запятой может вскоре изменить некоторые из наших представлений о том, что является хорошим алгоритмом в той или иной конкретной задаче. Многие ухищрения, используемые для того, чтобы преодолеть эффекты ограниченной точности, становятся ненужными, когда появляется возможность проведения вычислений с удвоенной точностью. В этой главе попытаемся показать некоторую взаимосвязь между алгоритмами обработки сигналов и технологией интегральных схем. В разд. 1.2 рассмотрим некоторые задачи обработки сигналов, связанные со стационарными стохастическими моделями, или, что то же самое, задачи, приводящие к линейным уравнениям с теплицевыми матрицами. Эта специальная форма уравнений, одна из первых в статистической обработке сигналов, была рассмотрена в работах Винера и Левинсона в 40-50-х гг. Однако технологические ограничения на емкость элементов памяти, как об этом уже упоминалось, привели к тому, что в 50- 60-х гг. основное развитие получили устройства обработки типа калмановского фильтра с фиксированной памятью (см., например, [26]). Алгоритм Левинсона продолжали применять в задачах обработки сигналов в геофизике (сейсмологии), где было возможным использование больших вычислительных ресурсов; в конце 60-х гг. он опять нашел свое применение в задачах синтеза речи (Атал, Шредер, Итакура, Саито 11 и др.). Мы разовьем их выводы в разд. 1.2, показав, как теплицева форма при современной технологии СБИС и возможно оптической и волновой технологии приводит к очень изящным результатам. Хотя предположение о стационарности во многих случаях упрощает анализ, часто встречаются ситуации, когда это предположение несправедливо. Мы рассматриваем такие ситуации в разд. 1.3 и показываем, как некоторые относительно новые теоретические исследования позволяют сохранить преимущества стационарного приближения для некоторых нестационарных задач обработки сигналов за счет использования дополнительной памяти. По различным причинам изложение будет кратким и не будет содержать доказательств, которые можно найти в работах, упомянутых в списке литературы. Цель состоит в том, чтобы проиллюстрировать некоторые аспекты развивающейся взаимосвязи теории и техники обработки сигналов. Книга содержит много других примеров на эту тему. 1.2. НЕКОТОРЫЕ АЛГОРИТМЫ ДЛЯ ТЕ Г ЛИЦЕВЫХ МАТРИЦ Хорошо известные в настоящее время методы кодирования с линейным предсказанием (КЛП) для анализа речевых сигналов основаны на гипотезе о том, что речевые сигналы могут быть смоделированы как результат прохождения белого шума через линейный инвариантный во времени фильтр. Данная гипотеза основывается на том, что процессы переноса информации, по существу, случайны (на это впервые обратил внимание Норберт Винер). Применительно к анализу речевых сигналов воздух, выходящий из легких, можно представить как белый шум, который модулируется колебаниями голосового тракта (голосовых связок, нбса, губ) и создает звуковые волны. Линейный инвариантный во времени фильтр может быть смоделирован различными способами, однако по разным причинам первоначально внимание было сосредоточено на использовании моделей, в которых речь представляется в виде стационарного дискретизированного по времени случайного процесса авторегрессии: Г, + АКщ ,у, , +----+ А (V, и у, . N = eNt,, где {eNt} - белый шум с нулевым математическим ожиданием. Проблемы, возникающие при моделировании, состоят в выборе порядка N, значений коэффициентов {Ал} и дисперсии* шума Ад, для наилучшего описания исследуемого речевого сигнала [у,, г > 0}. Обычная процедура состоит в получении выборочной ковариационной функции Ri = £[),),-,] стационарного процесса jjf, / >0j и нахождении коэффициентов} Л ,Vi}из уравнения Юла-Уокера = [0 -• 0 /].(1.1) AN, 1 Л Допущения, лежащие в основе этой формулировки, более подробно исследуем в разд. 1.3 и найдем некоторые основания, чтобы не согласиться с ней. Однако одна из причин широкого распространения формулировки (1.1) состоит в том, что специальная с постоянными элементами вдоль диагоналей (теплицева) форма матрицы в уравнении (1.2) приводит к удобному быстрому рекурсивному алгоритму решения уравнения - алгоритму Левинсона1 :
(1.2) где ANiz) = Акл + ANi иjz + • - • + AN< ,2л 1 + zN; BN(z) = A„ NzN + АКч {zN 1 + • A ,z + 1 ; £ . ,v Rl + Ay у ji?2 + " + AN (Rv + Ry+1 RN+= R%(1 - j); Re0 =NR0 . Смысл состоит в последовательном нахождении решения {AN {. Л= = 0, 1,. .. }, причем основные вычислительные сложности связаны с нахождением скалярного произведения в формуле для fc*r+i> вычисление которого требует Л операций умножения и Л - сложения. Таким образом, для вычисления последовательности . .. , kpj] потребуется 1 + 2+ + N = N(N -i-\)I2 или О (Л/2) элементарных операций вычисления, что на порядок меньше, чем О (Л3) операций вычисления, необходимых для решения произвольной системы линейных уравнений, не имеющей специальной теплицевой структуры (1.1). Алгоритм Левинсона можно использовать для создания семейства авторегрессионных моделей возрастающего порядка, и нам необходимо только каким-то образом определить этот подходящий порядок. Для этого существуют различные критерии (например, информационный критерий Акайка), а также некоторые соображения (например, практические конструкторские ограничения на реализацию интегральной схемы), которые здесь не рассма г-риваются. Следует обратить внимание на то, что алгоритм Левинсона обладает особой структурой, которая обеспечивает определенную гибкость в выборе порядка. Традиционным устройством нахождения eN t является трансвереальный фильтр (например, на основе линии задержки с отводами) с коэффициента- (1.3а) (1.36) 1 Предложен Левинсоном впервые в 1947 г. [37]; с этим алгоритмом могут быть связаны и некоторые другие имена, в частности имя Дурбина [18]. Можно отметить, что формула (1.2) представляет, по существу, классическую рекуррентную формулу для ортогональных полиномов на окружности единичного радиуса [57] .
+ чм,о
а) Рис. 1.1. Реализация фильтра в виде линии задержки с отводами: а - выбеливающий фильтр; б - моделирующий фильтр б) 3 ми lA дгд), ..., AN j/j (рис. 1.1); необходимо только заметить, что во избежание недоразумений передаточной характеристикой фильтра для расчета cN t должна бытьHeAN(z),a А, + An. ш Однако если нет уверенности в выборе порядка, а необходимо подсчитать, скажем, £д>+2 t, то уже нельзя только повысить порядок трансверсаль-ного фильтра, а следует заменить все коэффициенты А дг0,... ,AN N] на { Л+2,0 • • • N+2, N+2 } • Существует много примеров, когда, прежде чем остановиться на выборе определенного порядка Л, желательно оценить отклик фильтра в некотором диапазоне изменения величины N, а это неудобно делать при трансверсальной реализации фильтра. Из выражения (1.2) следует, что коэффициенты {&,-,/ = 1,... ,NJ вместе с условием А0 (z) =В0 (z) = = 1 дают другую параметризацию фильтра: знание этих величин позволяет определить AN(z) и, следовательно, коэффициенты {AN Л из (1.2). Если есть желание выбрать другой порядок, скажем N+2, то в этой параметризации придется добавить еще только два коэффициента {&дг+1, AA?+2} без изменения ранее найденных величин. Это свойство инвариантности параметризации {kj}можно использовать осуществляя реализацию фильтров в терминах {к;, Кг <Л} , а не {an t }. Из выражения (1.2) следует, что фильтр можно создать в виде каскадного соединения решетчатых секций, как на рис. 1.2,с, или в некотором нормализованном виде (см. далее формулу (1.5)), как на рис. 1.2,6. С помощью методов теории сигнальных графов легко осуществить обращение решетчатых фильтров. Результат такого преобразования - моделирующий фильтр показан на рис. 1.3. Он имеет вид дискретной длинной линии и помогает объяснить, почему {к{} часто называют коэффициентами отобра- При такой физической интерпретации предполагается, что должно выполняться условие <1, (1.4) 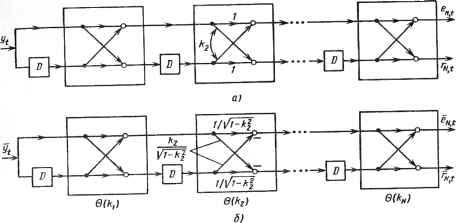 Рис. 1.2. Реализация выбеливающих фильтров в виде решетчатого фильтра: а - ненормализованный вид; б - нормализованный вид к2 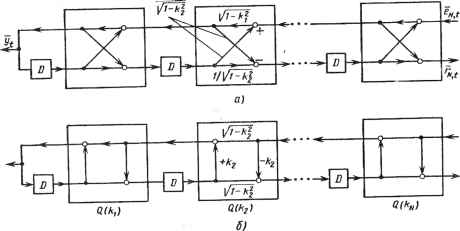 Рис. 1.3. Моделирующие фильтры: с - решетчатый фильтр с обратной связью - нормализованный вид; б - фильтр в длинной надписи которое следует также из (1.36) (так как значения дисперсии должны быть неотрицательными). На Az) должны быть наложены определенные ограничения: корни полинома z*A (z) должны лежать в круге единичного радиуса, однако это условие не так просто перевести на интервал изменения коэффициентов {Лд,По этой и другим причинам характеристики (нормализованного) решетчатого фильтра лучше аналогичных характеристик трансверсаль- 0 1 2 3 4 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












