Раздел: Документация
0 1 2 3 4 5 6 7 ... 78 [51] E. A. Robinson, "Dynamic Predictive Deconvolution," Geophys. Prospect., 25:779-797 (1975). [52] E. A. Robinson, "Spectral Approach to Geophysical Inversion by Lorentz, Fourier and Radon Transforms," Proc. IEEE, 70:1039-1054 (1982). [53] E. Satorius and i. Pack, "Application of Least-Squares Lattice Algorithms to Adaptive Equalization," IEEE Trans. Commun., C0M-2P:!36-142 (1981). [54] C. W. Schelin, "Calculator Function Approximation," Am. Math. Monthly, 90:317 -32.5 (1983). [55] I. Schur, "Uber Potenzreihen, die im Innern des Einheitskreises beschrankt sind," J. ReineAngew. Math., /47:205-232(1917). [56] H. Sexton, M. Shensa, and J. Speiser, "Remarks on a Displacement-Rank Inversion Method for Toeplitz Systems," Linear Algebra Appl., 45:127-130 (1982). [57] G. Szego, Orthogonal Polynomials, 4th ed., Colloquium Publications, 23, American Mathematical Society, Providence, R. I., 1975. Originally published in 1939. [58] J. E. Voider, "The CORDIC Trigonometric Computing Technique," IRE Trans. Electron. Comput., £C-8(3):330-334 (1959). [59] J. S. Walther, "A Unified Algorithm for Elementary Functions," Proc. 1971 Spring Joint Comput- Con/., 1971, pp. 379-385. [60] R. Wiggins and L. Brantingham, "Three Chip System Synthesizes Human Speech," Electronics, 5/(18):109-116 t1978). 2 ПРИМЕНЕНИЕ ПАРАЛЛЕЛЬНЫХ МАТРИЧНЫХ ПРОЦЕССОРОВ ДЛЯ ОБРАБОТКИ СИГНАЛОВ X. Уайтхаус, Дж: Спейзер, К. Бромли1 2.1. ВВЕДЕНИЕ Как было показано ранее, основные вычислительные процедуры при решении большинства задач обработки сигналов в реальном масштабе времени могут быть сведены к набору операций над матрицами [1 -3]. Он включает умножение матрицы на вектор, умножение матрицы иа матрицу и сложение, обращение матриц, решение линейных систем уравнений, приближенное решение линейных систем по методу наименьших квадратов, вычисление собственных значений, нахождение сингулярного разложения матриц. Широкие исследования в области вычислительных методов линейной алгебры привели к созданию двух устойчивых, хорошо документированных пакетов стандартных программ для выполнения этих операций с помощью однопроцессорных компьютеров последовательного действия. Один из этих пакетов, называемый UNPACK (4], предназначен для решения линейных систем уравнений и вычислительных задач, основанных на применении метода наименьших квадратов. Другой, называемый EISPACK [5], охватывает задачи вычисле- 1 Центр океанических систем ВМС, Сан-Диего, Калифорния нИя собственных значений. Эти алгоритмы по вычислительным затратам достаточно сложны и требуют примерно А3 или /V4 операций умножения для каждого набора из N входных отсчетов. Для сравнения современный алгоритм обработки сигналов - БПФ - требует только Alog2 Лопераций умножения и тем не менее его реализация в реальном масштабе времени на современных однокристальных арифметических процессорных модулях ограничивается полосой звуковых частот. Очевидно, что потребуется на порядок увеличить скорость вычислений, для того чтобы обеспечить выполнение в реальном масштабе времени этих перспективных алгоритмов. Несмотря на гигантские достижения за последнее десятилетие в технологии цифровых ИС, нельзя просто рассчитывать на дальнейшие успехи в производстве быстродействующих элементов вычислительных устройств. В настоящее время уровень технического развития кристаллов СБИС обеспечивает реализацию технологических размеров от 1 до 2 мкм. Целью фазы II программы ССИС (сверхскоростные ИС) Министерства обороны США служит уменьшение этих размеров до 0,5 мкм к 1987 г., что позволит увеличить функциональную скорость передачи данных (т.е. тактовую частоту, отнесенную к плотности компоновки) на кристалл от 5 1С)11 Гц до 1013 Гц вентиль/см2. По-видимому, потребуется по крайней мере еще три года усилий для такого повышения производительности, когда эта технология будет экономически выгодна. Так что можно ожидать немногим более 20-кратного улучшения функциональной скорости передачи данных кристаллов СБИС к 1990 г. Более того, в большинстве современных проектов показывается, что дальнейшее уменьшение размеров до 0,5 мкм и менее будет возможно только ценой значительных усилий. Авторы утверждают, что если исключить из рассмотрения непредвиденные в настоящее время успехи в технической реализации процессора сигналов, то увеличение на несколько порядков производительности процессора для обработки в реальном масштабе времени алгоритмов UNPACK и EISPACK должно осуществляться эффективным использованием параллелизма при вычислениях. Самым непосредственным способом реализации параллельной обработки сигналов является простое присоединение ряда процессоров к общей шине. Действительно, большинство современных серийных микропроцессорных комплектов отличается такой "мультипроцессорностью". Однако производительность повышается линейно с увеличением числа процессоров только до тех пор, пока не наступают ограничения, связанные с проблемами соединения с общей шиной. Согласно хорошо известному предположению Минского для широкого класса алгоритмов конфликт между А процессорами с коллективным распределением ресурсов, соединенными с общей шиной, ограничивает повышение- производительности величиной log 2 Л. Современные конструкторы "суперкомпьютеров" использовали ряд параллельных структур и достигли повышения производительности в соответствии с законом А м дал a (Amdahl). Nj\og2N. В 1978 г. С. Т. Кунг (Н. Т. Kung) представил свою пионерскую работу по архитектурам систолических процессорных матриц, в которой был достигнут исключительно высокий коэффициент повышения производительности, равный N [6] . 2S 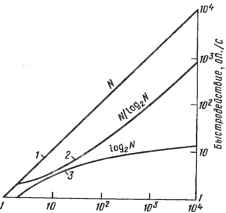 Число процессоров Рис. 2.1. Графическое представление увеличения быстродействия, обеспечиваемого перспективной архитектурой работающих одновременно N процессоров: / - 100%-ная производительность (систолические решетки); 2 - закон Амда-ла (суперкомпьютеры); J - предложения Минского (ограничения, связанные с конфликтами на шине в многопроцессорных системах) На рис. 2.1 графически представлено увеличение быстродействия при параллелизме для трех случаев. В работах [1-3] рассмотрены параллельные архитектуры и сделан вывод, что систолические и волновые матричные архитектуры [6, 7] обеспечивают наиболее перспективную совокупность характеристик при использовании технологии СБИС и ССИС для обработки сигналов в реальном масштабе времени: параллелизм на уровне модулей с пропускной способностью, прямо пропорциональной числу вычислительных ячеек, простое управление, синхронный поток данных, локальные связи, достаточную гибкость для выполнения матричных операций, необходимых при обработке сигналов. Систолические и волновые процессоры имеют линейную структуру для умножения матрицы на вектор и решения линейных уравнений с треугольными матрицами коэффициентов, а также гексагональную структуру для матричных операций умножения-сложения и £<У-разложения матриц. Эти архитектуры особенно привлекательны в случае разреженных ленточных матриц. В этой главе обсуждаются процессоры новой архитектуры для умножения заполненных матриц, для операций над блочными матрицами, а также прикладные задачи вычисления функций неопределенности. Читателя, интересующегося аппаратурной реализацией систолической и волновой архитектур, отсылаем к работе [8], где описана одномерная процессорная матрица, содержащая 200 МОП-кристаллов, к работе [9], где описан макет двумерной процессорной матрицы, к гл. 8 этой книги, посвященной заказной систолической БИС, к гл. 22, в которой содержится описание двух заказных систолических СБИС, и к гл. 17, где имеется описание кристалла СБИС для решения теплицевой системы уравнений [10]. Читателя, интересующегося систолическими матричными структурами для реализации более сложных алгоритмов, чем те, которые описаны здесь, отсылаем к работам: [11] - по воп- 30 росам приведения матрицы к треугольному виду, [12] - о сингулярном разложении, [13, 14] - о проблеме собственных значений и [10] - о решении теплицевых систем уравнений. 2.2. ЗАДАЧИ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ Рассмотрим метод наименьших квадратов применительно к задачам трех типов: детерминированной, стохастической с известными вторыми моментами и стохастической с неизвестными вторыми моментами, которые надо оценить. Покажем, что стохастическая задача с оцениваемыми вторыми моментами в вычислительном отношении идентична детерминированной задаче и поэтому основной метод решения для многих случаев обработки сигналов в реальном масштабе времени может быть основан на формировании и решении нормальных уравнений путем систолических матричных умножений, умножения матрицы на вектор и обращения матриц. Известны другие методы решения задач наименьших квадратов [19], а в работе [11] рассматривается систолическая реализация. Детерминированная задача состоит в выборе вектора х таким образом, чтобы минимизировалось значение е2 в уравнении е? = Ах-у2 =хгА7Ах-2у7Ах+у2,(2.1) где А - известная матрица, а у - известный вектор, индекс Т обозначает транспонирование матрицы или вектора. Стохастическая задача наименьших квадратов состоит в выборе детерминированного весового вектора w для минимизации средней квадратичес-кой ошибки el: el = £(w7z - d)2 = WJ Rzw- 2RJ1 w + E(d2),(2.2) где z - случайный вектор; d - случайная величина. Скалярная случайная величина wz представляет собой линейную комбинацию компонентов случайного вектора z и используется как линейная оценка случайной величины d. Математическое ожидание обозначается символом Е, через Rz обозначена матрица вторых моментов случайного вектора z: Rz =EzzT. Аналогично вектор R2 определяется как Kdz = E(dz). Для того чтобы сравнить две задачи, предположим, что А имеет размер (NXS), х- (5X1), у- (/VX1), z-(SXl), w-(SXl). Для стохастической задачи наименьших квадратов с оценкой вторых моментов предположим, что наблюдаются N отсчетов случайного вектора / и случайной величины d, например z (и, s) и d(n) при и = 1,...,Nhs = 1, ,S. Стандартные несмещенные оценки вторых моментов даются выражениями =77 5>«.*iM",*2).(2.3) (R„JS1 = £s,)= j- £ zT(Sl, n)d{n),(2.4) 31 ~ R эквивалент дсхерми„ирова1Ш0Й и
(Ed2) = ~i«.(2.5) Соответствующая ошибка для оценки d через wrz определяется формулой е2 = wrRz w-2R§j w + (Ed2).(2.6) Соотношения, приведенные в табл. 2.1, иллюстрируют вычислительную эквивалентность стохастической задачи наименьших квадратов с оценкой вторых моментов и соответствующей детерминированной задачи. Поэтому достаточно рассмотреть вычислительные методы только для детерминированной задачи наименьших квадратов. 2.2.1. Применение метода наименьших квадратов к задачам гидролокации Метод наименьших квадратов применяется при решеьии трех проблем улучшения характеристик гидролокатора: подавления шума, подавления помех и спектрального анализа по методу максимума энтропии. При решении проблемы подавления шума полагают, что выходной сигнал гидрофона представляет собой линейную комбинацию напряженности окружающего акустического поля с составляющими локальных источников шума, такими, как, например, шум двигателей собственного корабля. Чтобы выделить только сигналы шума, вблизи от двигателей можно установить вспомогательные датчики. Для дальнейшего улучшения этого метода на входы устройства подавления могут быть поданы задержанные копии сигналов каждого эталонного источника шума. Тогда линейные комбинации этих задержанных копий будут аппроксимировать отфильтрованный сигнал шума, принятый гидрофоном от источника после его распространения по корпусу корабля. Задача подавления помех аналогична задаче подавления шума, за исключением того, что входными сигналами адаптивного устройства компенсации являются выходные сигналы лучеобразующих устройств. Для формирования одного луча без помех в заданное положение направляется обычный луч и формируется S "нулевых лучей". Чувствительность нулевых лучей равна нулю при приеме сигнала с заданного направления, и они используются для приема помех. В общем случае требуется столько линейно независимых 32 нулевых лучей, сколько помех необходимо подавить. Если выходы каждой из этих лучеобразующих схем объединить через весовой сумматор с выходом лучеобразующей схемы, принимающей сигнал с заданного направления, о минимизация общей мощности уменьшит помехи в выходном сигнале. Если составляющие помехи не коррелированы с сигналом, принимаемым с заданного направления, то вклад полезного сигнала в выходную мощность остается постоянным. Однако при определенных условиях это допущение может нарушаться. При многолучевом распространении полезный сигнал может быть принят нулевым лучом так же, как и лучом, ориентированным в заданном направлении. В этом случае подстройка весовых коэффициентов, направленная на уменьшение общей мощности выходного сигнала, может привести к уменьшению как помех, так и полезного сигнала. Подавление шума и помех, как правило, осуществляется адаптивными трансверсальнымк фильтрами, реализующими метод градиентного спуска - алгоритм минимизации средней квадратической ошибки (МСКО) Уидроу [15]. Цель таких способов реализации - обеспечить адаптацию при небольшом числе операций умножения, т.е. при относительно простой аппаратурной реализации. Скорость адаптации уменьшается при большом разбросе собственных значений ковариационной матрицы данных [16], что, к сожалению, имеет место при сильных источниках помех. Это может привести к времени сходимости, значительно превышающему период, в течение которого процессы, воздействуюшие на систему подавления, можно считать стационарными. В этом случае более быстрая сходимость может быть получена непосредственным обращением ковариационной матрицы выборок и решением нормальных уравнений, что приведет к более эффективному (в статистическом смысле) использованию имеющихся данных [17]. Современные методы спектрального анализа обеспечивают повышенную разрешающую способность при использовании параметрической модели сигнала. В методе максимума энтропии сигнал моделируется как выходной сигнал фильтра, имеющего только полюсы, на вход которого подан белый шум [18]. Обратным такому фильтру служит трансверсальный фильтр, преобразующий сигнал в белый шум, весовые коэффициенты которого рассчитываются путем решения задачи линейного прогноза сигнала ка один шаг вперед. Известно, что для стационарного процесса ошибка прогноза по методу наименьших квадратов представляет собой белый шум. Тогда оцениваемая функция спектральной плотности пропорциональна величине, обратной квадрату передаточной функции прогнозирующего фильтра. Этот метод спектральной оценки, обеспечивающий повышенную разрешающую способность в том случае, когда модель применима и отношение сигнал-шум достаточно велико, может быть также использован для формирования луча [18]. Задачи, решаемые с помощью метода наименьших квадратов применительно к подавлению шума, подавлению помех и спектральному анализу методом максимальной энтропии, езедены в табл. 2.2. 0 1 2 3 4 5 6 7 ... 78 |












