Раздел: Документация
0 ... 2 3 4 5 6 7 8 ... 78 Таблица 2.2. Таблица соответствия величин в методе наименьших квадратов применительно к гидролокации Задачаzd Подавление шумаzit...,zs (эталонные ис-Сигнал + шум точники шума) Подавление помех (адаптив- Ь,,..., Ьу (выходные сиг- Ь0 (выходной сигнал луча, ная обработка с фиксирован- налы "нулевых лучей")ориентированного в задангом ными лучами)направлении) Спектральный анализ мето- х,, . . . , xs (временные от-ху+1 дом максимума энтропии счеты сигнала) 2.3." ВСТРЕЧНО-ПОТОЧНЫЙ ПРОЦЕССОР Систолическую архитектуру можно рассматривать как результат реализации последовательности рекурсивных алгоритмов с помощью сети идентичных (или большей частью идентичных) вычислительных ячеек. При вычислении произведения матриц С = АВ каждый элемент cpq матрицы С является скалярным произведением строки А и столбца В: N срч= Х«РА«(2.7) s= 1 Матричное умножение можно также рассматривать как рекуррентную процедуру: С = °-(2.8 а) ср1 = с%, " + aps bsq при s = 1, ..., N,(2.8 б) где cj,* - искомый результат. Такие операции сложения могут быть представлены в виде рекурсивных выражений, содержащих промежуточные члены, перемещающиеся вдоль структуры, или в виде накопления частичных сумм "с замещением" [4,5]. Главной систолической ячейкой для операций линейной алгебры является процессор скалярного произведения [6], изображенный на рис. 2.2 в виде прямоугольной и гексагональной структур [6]. В оставшейся части этой главы будет использоваться гексагональное представление систолической ячейки. При соединении порта Свых через цепь обратной связи с Свх конфигурация ячейки будет особенно хорошо приспособлена для вычисления скалярного произведения по формулам (2.8). Если предположить, что Свх = = 0 в момент времени п- 0, то при n=N значение Свых будет искомым скалярным произведением. Необходимо обратить внимание на то, что значение суммы в выражении (2.7) остается неизменным при перестановке индексов слагаемых. В этой главе в дальнейшем будут использованы две специальные перестановки: обратная и циклическая. Встречно-поточный процессор (рис. 2.3) производит перемножение матрицы на матрицу или умножение-сложение с помощью процессора, состоящего 34 "их Sx свх ь8ых о цвых ввых Свых 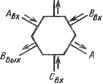 "П "23 ьп ьгг ьзз Jn) =Й1п-П в("1 - в(п» °ьы* в* r(» гС-П + л!п-Г) вт-п ь0ых идх лВх °вх ч 1„ а,
Рис. 2.3. Перемножение полных матриц встречно-поточным процессором Рис. 2.2. Геометрическое представление процессора для вычисления скалярного произведения из ячеек, подобных той, которая показана на рис. 2.2, осуществляя вычисление частичных сумм с замещением. Элементы строк матрицы А и элементы столбцов матрицы В вводятся в процессор через память интерфейсных уст-►ройств. Последовательные строки и столбцы вводятся с единичной задержкой так, что в памяти имитируется набор линий задержки, создавая сдвиг на один временной такт между вводом последовательных строк и столбцов. Каждая ячейка процессора имеет конфигурацию, показанную на рис. 2.2, и вычисляет сумму скалярного произведения и начального значения Свых. •Для вычисления произведения матриц значение сп принимается равным нулю в начальный момент времени, с2, и с12 принимаются равными нулю в момент времени 1, с13, г22 и с31 принимаются равными нулю в момент времени 2 и т. д., элементы А-й побочной диагонали принимаются равными нулю в момент времени к - 1. В момент времени k+N скалярные произведения всех элементов, соответствующих А-й побочной диагонали, будут записаны в памяти. Если элементы изначально не равны нулю, то производится матричное умножение-сложение: Сконеч = Снач +А *В. Запись последнего члена завершается за время Т= (А- 1) + (А- 1) +А=ЗА-2. Это означает, что встроечно-поточный процессор производит матричное умножение или умножение-сложение заполненных АХ Лматриц за время ЗА- 2 при использовании А2 ячеек, обеспечивая выигрыш в эффективности приблизительно в четыре раза по сравнению с обычной гексагональной систолической структурой матричного умножителя. Поскольку при обработке сигналов часто требуется перемножение заполненных матриц, этот выигрыш является значительным.. Встроечно-поточный процессор вычисляет матричное произведение (1.1} согласно рекуррентным соотношениям ди-п + №- 1)1 = о, Ь «) + (.; !) + № 1)Л> где с(" обозначает содержимое ячейки (j,k) в момент временип. (2.9) (2.10) В момент времени п = (/- 1) + (к - 1) +N ячейка (j,k) содержит (/,£)-й элемент матричного произведения. Если эффективность определить как число выполняемых умножений-сложений Эффективность =-, (2.П) число ячеек X суммарное время то можно увидеть, что при неконвейерном режиме эффективность встречно-поточного процессора составляет АГ(ЗЛГ- 2), т. е. больше 1 /3. Встречно-поточный процессор можно также использовать для умножения прямоугольных матриц. Если А имеет размер (УХА), а В - размер (NXК), то необходимый размер процессорной структуры равен J ХКн последнее вычисление заканчивается в момент времени N+ (J - 1) + (К- I) =N+J +К- 2. В этом случае эффективность равна (NJK) jJK(N+J +К- 2) =N/(N+ J+K--2) и велика, когда N велико по сравнению cJ+K. В дальнейшем в этой главе будет показано, что часто имеется возможность конвейеризовать матричные умножения с помощью встречно-поточного процессора с достижением эффективности, близкой к 100%. Далее рассмотрим некоторые специальные случаи матричных умножений с использованием процессоров рассмотренного типа. 2.3.1. Вычисление внешнего произведения векторов с использованием встречно-поточного процессора Вычисление внешнего произведения двух векторов представляет собой важный вырожденный случай умножения матрицы на матрицу. В векторной и покомпонентной записи оно определяется выражениями С = иЬт, «1 aib* «2 Ь\* о3 Ь% а2Ь% иъЬ* (2.12а) (2.126) (2.13) Внешнее произведение двух векторов используется, например, при вычислении преобразований Хаусхолдера [19] и функции неопределенности. Вычисление внешнего произведения встречно-поточным процессором иллюстрируется на рис. 2.4. Необходимое время вычисления составляет 2N~ 1. 2.3.2. Умножение ганкелевой матрицы на произвольную матрицу Умножение ганкелевой матрицы на произвольную матрицу определяется выражением i-... (2.14)
36 i Расширитель магистрали a3i Q32 а31
Рис. 2.4. Умножение ганкелевой матрицы на произвольную матрицу Рис. 2.5. Умножение ганкелевой матрицы на произвольную матрицу с использованием встречно-поточного процессора с расширителем магистрали Оно используется, например, при формировании междуканалыюй функции взаимной корреляции либо как одна из частей вычисления функции неопределенности. Поскольку ганкелева матрица имеет одинаковые элементы на побочной диагонали, она полностью определяется своими значениями крайнего левого столбца и нижней строки. И, следовательно, ганкелева (NXN)-матрица может быть представлена в виде вектора длиной 2N- 1. Для того чтобы использовать такую форму сжатия данных без увеличения времени, необходимого для загрузки встречно-поточного процессора, загрузку одной строки процессора производят с помощью специального "расширителя магистрали" (рис. 2.5). Поскольку длинный вектор с помощью расширителя магистрали преобразуется в эквивалентную входную матрицу, требуемое время вычисления для такой структуры в точности такое же, как и для общего случая умножения матрицы на матрицу с помощью структуры, приведенной на рис. 2.3 (т.е. равно ЗА- 2). 2.3.3. Умножение теплицевой матршгы на произвольную матрицу Элементы теплицевой матрицы, расположенные на какой-либо диагонали, одинаковы, поэтому ее перемножение с произвольной матрицей очень похоже на умножение ганкелевой матрицы на произвольную матрицу, но по смыслу больше соответствует многоканальной свертке, чем корреляции. Это иллюстрируется выражением Ь0 Ь , АТ = «и «21 «31 22 12 1ъ -2 -1 О (2.15) 37 а„ ап аа а2/ агг 1123 - аи азгазз-
Расширитель магистрали -J- Расширитель магистрали bo Ь-2 Рис. 2.6. Умножение теплицевой матрицы на произвольную матрицу с использованием встречно-поточного процессора с расширителем магистрали
Использование двойной асимметрии а. Рис. 2.7- Вычисление асимметричного внешнего произведения с использованием встречно-поточного процессора с расширителем магистрали а аппаратурная реализация с использованием встречно-поточного процессора с расширителем магистрали показана на рис. 2.6. Необходимое время вычисления составляет 3W- 2. 2.3.4.Асимметричное внешнее произведение векторов Вычисление асимметричного внешнего произведения1, представленного выражением cjk = aih.i-k,(2.16) полезно при вычислении функции неопределенности. Оно может быть реализовано как частный случай вычисления внешнего произведения с помощью встречно-поточного процессора с расширителем магистрали, как показано на рис. 2.7. Необходимое время вычисления равно 2Л- 1. 2.3.5.Вычисление тройного асимметричного внешнего векторного произведения Тройное асимметричное произведение трех векторов определено выражением N 1 Р{и, s) = £.(2.17) Подобно асимметричному внешнему произведению, тройное произведение также оказывается полезным при вычислении функции неопределенности. 1 В оригинале "skewed outer product". Устоявшегося термина для конструкции (2.16) в литературе на русском языке нет. - Прим. ред. 38 Диагональная часть P(s, s) асимметричного тройного произведения называется "тройной сверткой" и используется при формировании лучей [20]. Оно может быть вычислено как асимметричное внешнее произведение векторов а и b с последующим умножением на ганкелеву матрицу, соответствующую с. Полное время вычисления составляет SN- 3. 2.3.6. Двумерное дискретное преобразование Фурье с использованием матричного процессора Умножитель матриц размера NXN может осуществить дискретное преобразование Фурье (ДПФ) N векторов размерности N как одно матричное умножение. Если F - матрица ДПФ, определяемая выражением (2.18), то FX - матрица, столбцы которой представляют собой ДПФ столбцов матрицы X, a XF - матрица, строки которой являются ДПФ строк матрицы X. Аналогично FXF представляет собой двумерное ДПФ матрицы X: Fw = e2"M/v.(2.18) 2.3.7. Вычисление функции неопределенности с использованием встречно-поточного процессора с расширителем магистрали Функция неопределенности A12(r,f) = \g1(t)g*2(t + т)е~№ dx(2.19) является обобщенной функцией взаимной корреляции, зависящей как от сдвига относительной частоты, так и от задержки [21]. В табл. 2.3 показано, как вычисление функции неопределенности реализуется современными оптическими процессорами и как можно привести эти вычисления к комбинации матричных операций, описанных в этой главе. Таблица 2.3. Методы вычисления функции неопределенности Двумерное преобразование Фурье т-срез Временное интегрирование Пространственное интегрирование J[9,()9!(«)e"J2""]e-J2"(»+"1 dt du 1.0,(0<?! С + T)]eJ2-" Л е~*я J [0(Ое->"][й<1 + т)>/* >г dt [ff,()e-/2-/][ff*(f + т)]Л 0 ... 2 3 4 5 6 7 8 ... 78 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












