Раздел: Документация
0 ... 4 5 6 7 8 9 10 ... 78 Разрешающая способность по частоте в обычных методах, основанных на преобразовании Фурье, примерно обратно пропорциональна объему выборки. Поэтому для улучшения разрешающей способности необходимо ввести некоторые дополнительные ограничения (или априорную информацию). С этой целью в современных методах данные моделируются как процесс на выходе линейной системы, на вход которой подан белый шум. Когда такая модель соответствует реальному сигналу, эти методы приводят к улучшению спектральных оценок. Цена, которую приходится платить за это улучшение, как правило, состоит в увеличении сложности вычислений по сравнению с таковой при обычных методах, основанных на использовании БПФ. Однако с появлением СБИС стоимость вычислительной аппаратуры уменьшилась, что явилось существенным стимулом для использования и развития с целью улучшения ее характеристик более усложненных в вычислительном отношении методов спектрального анализа. В этой главе вначале обсудим обычные методы анализа энергетического спектра, а затем в следующих разделах сосредоточим внимание на современных методах, делая акцент на тех из них, которые подходят для разрешения узкополосных сигналов. Более подробное обсуждение этого вопроса можно найти в работах [3,4]. 3.2. ОБЫЧНЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА [5] Предположим, что процесс х(п) является стационарным в широком смысле действительным дискретным стохастическим процессом с нулевым математическим ожиданием. Нас будет интересовать спектр мощности, который представляет собой распределение мощности по частотам и определяется как [6] До>)= 1 гхх(п)е">(31) п - - ОС где гхх (т) - корреляционная функция: гхх(т) = Е[х(п)х(т + п)] , Е[-] - оператор математического ожидания. Косвенный подход Блэкмана и Тьюки к оценке спектра мощности состоит в получении вначале оценки корреляционной функции на конечном интервале, а затем в применении преобразования Фурье, по существу, в предположении, что остальные значения равны нулю: м - 1 РвтМ= I иФ"-(3-2) Очень часто перед преобразованием Фурье корреляционная функция подвергается весовой обработке (взвешиванию) функцией окна (для сглаживания перехода к нулевым значениям) м-1 Рш(о)) = I еЛн)Щп)е{ i<0", -(3.3) Спектр мощности можно определить и другим методом. На основании классической теоремы Винера-Хинчина [5] спектр мощности эргодическо-го процесса определяется как 1 Р(со) = lim Е N - 1 X, х(п)е ima (3.4) Это выражение приводит к более непосредственному методу вычислений. На практике объем выборки N конечен; поэтому прямой метод вычислений осуществляется согласно (3.4) с конечным значением N, операция усреднения по ансамблю опускается. Оценка спектра мощности, основанная на прямом методе, называется периодограммой (термин, впервые введенный Шустером [7]) и определяется как квадрат результата преобразования Фурье от данных конечной длины: N - 1 п = 0 (3-5) Периодограмма совпадает с косвенной оценкой по формуле (3.2) в том случае, когда используется следующая смещенная оценка корреляционной функции: ] N ml = Tr X х(п)х{п + т). А „ = о Рассмотренные методы стали популярны вследствие высокой эффективности вычислений по алгоритму БПФ. Однако предположение о нулевом значении данных и корреляционной функции за пределами интервала наблюдения неестественно и ограничивает разрешающую способность величиной, приблизительно обратно пропорциональной объему выборки данных. Кроме того, резкий переход к нулю вызывает появление больших боковых лепестков в оценке спектра (явление Гиббса). Правильный выбор функции окна может улучшить статистическую стабильность оценки и снизить уровень боковых лепестков, но ценой дальнейшего ухудшения разрешающей способности. Для более детального рассмотрения компромисса между разрешающей способностью и уровнем боковых лепестков при выборе функций окна мы отсылаем читателя к работам [5, 8, 9]. Можно показать, что как прямые, так и косвенные оценки спектра мощности несостоятельны, т.е. их дисперсия не стремится к нулю при увеличении объема выборки [5]. В работах [10, 11] с целью улучшения асимптотических статистических свойств оценки спектра независимо было предложено кусочное усреднение как своего рода усреднение по псевдоансамблю. В этом случае данные разделяются на сегменты, которые могут перекрываться, и спектр мощности вычисляется для каждого сегмента. Результирующий спектр мощности получается усреднением по всем сегментам. Однако при этом разрешающая способность ухудшается еще больше. И так как в большинстве интересующих нас случаев объем выборки весьма мал, метод посегментного усреднения для них неприемлем. Итак, к достоинствам всех традиционных методов спектрального оценивания относится высокая вычислительная эффективность алгоритма БПФ. но они не обеспечивают необходимой разрешающей способности. Разрешение по частоте ограничено из-за фундаментального соотношения неопределенности величиной, обратной интервалу корреляции в дискретном преобразовании Фурье. Следовательно, единственное средство достижения высокой разрешающей способности заключается в том, чтобы, располагая малым отрезком корреляционной функции, продолжить ее за пределы данного отрезка, основываясь на некоторых априорных, данных о входном процессе. Современные методы моделирования данных, как данных на выходе линейной системы, на вход которой подан белый шум, по существу, обеспечивают экстраполяцию корреляционной функции за пределами интервала наблюдения. 3.3. МЕТОДЫ, ОСНОВАННЫЕ НА МОДЕЛЯХ ИССЛЕДУЕМЫХ ПРОЦЕССОВ Во многих практических случаях физическая обстановка, обусловливающая формирование отраженного сигнала, может быть достаточно точно смоделирована линейной системой невысокого порядка. Например, известно, что при моделировании речи хорошей моделью механизма генерирования речевых сигналов является линейная система, формирующая процесс авторегрессии из белого шума. В методах, основанных на моделях, такая априорная информация используется для улучшения разрешающей способности по частоте. При моделировании обычными методами предполагается, что корреляция равна нулю за пределами интервала наблюдения, но на практике, в особенности когда сигналы узкополосные и корреляционная функция близка к периодической, такое предположение совершенно не соответствует действительности. В рассматриваемых методах корреляционная функция продолжается за пределы интервала наблюдения с помощью некоторых рекуррентных соотношений, определяемых параметрами модели. Эти параметры, получаемые на основе анализа корреляционной функции в пределах интервала наблюдения, полностью определяют ее поведение за пределами интервала, а также соответствующий спектр мощности. Следовательно, оценка спектра в современной постановке основана иа опенке параметров модели, а разрешающая способность таких параметрических спектральных оценок очень высока, если модель выбрана удачно. В общем случае в линейной системе с рациональной передаточной функцией связь между входной и выходной величинами описывается линейным разностным уравнением рч y(t) - V a.yit - 1) + £ /,г</ - i) + lis),(3.6) где входной величиной является {u(f)}, а выходкой {т> (г) }. Эта модель известна как модель авторегрессии скользящего среднего (АГСС). 48 Передаточная функция такой системы имеет вид H(z) = R(z)/A(z), где B(z) = 1 + I М~ ; Aiz) =1-1 a,-z-. i-1i=l В том случае, когда входной величиной -[и (г)} является белый шум с дисперсией а2, спектр мощности у (г) представляет собой /(<•>) = S(z) где S(z) = o2II(z)H(z >) = о2 :~-rrj(3.7) Функция 5(z) является также двусторонним z-преобразованием корреляционной функции у (г) в интервале от -°° до 00 : Ж*)= I r(k)z-k. к = - ж Если h(n) - импульсная характеристика системы, то H(z~l) является z-преобразованием "инвертированной во времени" последовательности h (-п). Следовательно, согласно выражению (3.7), если входное воздействие системы (г) описывается последовательностью a2h (-и), выходная последовательность будет представлять собой корреляционную функцию г (ш). Это означает, что r(m) = ]Г щ rim - /) 4- а2 £ Ь,- h{ - т + /).(3.3) i=l« = 0 Однако поскольку импульсная характеристика h (и) представляет собой каузальную последовательность, то h (-m+i)=0 для всех m>i. Как результат этого выражение (3.8) упрощается и принимает вид г(т) - ]Т a.; r(m - i) для всех т > ц.(3.9) i= 1 Таким образом, при линейной модели с рациональной передаточной функцией задание р последовательных значений корреляционной функции позволяет однозначно продолжить ее до бесконечности с помощью рекуррентного соотношения и поэтому модели АРСС могут существенно улучшить разрешающую способность. Представляет интерес частный случай общей модели (3.6), когда A (z) -= 1. Такую модель обычно называют моделью скользящего среднего (СС). Длительность корреляционной функции при такой модели ограничена, что не позволяет получить лучшую разрешающую способность по частоте, чем при методах преобразования Фурье. 3.3.1. Модели авторегрессии Более известная модель, используемая при спектральном анализе, описывается как частный случай выражения (3.6), когда В (z) = 1: >()= i,a,y(t- 0+ v(t).(3.10) Здесь выходная функция y(t) формируется как линейная регрессия своих прошлых значений, и поэтому такая модель известна как модель авторегрессии. (Кстати, общая модель, описываемая формулой (3.6), составлена из моделей авторегрессии и скользящего среднего и поэтому называется моделью авторегрессии скользящего среднего.) В моделях авторегрессииB(z) - 1, поэтому Р[аз) = с2 1 A(z)A(z~l) и рекуррентное соотношение (3.9) выполняется при всех к~>0: р г(к) = Х"."№ -)> к>0. i - 1 При к = 0 рекуррентное соотношение (3.9) имеет вид г(0)= fa-O + rr2. г - 1 Задавая М значений корреляционной функции {г(к)}, где М>р, можно оценить параметры {аг- } модели авторегрессии из приведенных рекуррентных уравнений для первых р значений из к. Они известны как уравнения Юла-Уокераили нормальные уравнения, иногда их называют уравнениями Винера-Хопфа в дискретном времени. В матричной форме они имеют вид
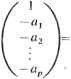 о 0 0 0 (3.11) LKp) Kp-1) rip - 2) • ко) Таким образом, параметрическая оценка с использованием модели авторегрессии включает решение линейной системы с симметричной положительно определенной теплицевой матрицей, которое может быть выполнено очень эффективно с помощью уже известного алгоритма Левинсона [32, 34, 36 - 38,48]. Существует два способа обоснования модели авторегрессии. Первый состоит в том, что, поскольку передаточная функция авторегрессионной модели имеет только полюсы, передаточная функция инверсного фильтра имеет только нули и его структура в точности совпадает со структурой фильтра, формирующего на выходе ошибку прогноза. Кроме того, коэффициенты линейного прогнозирующего фильтра, которые минимизируют данную ошиб-50 ку, также удовлетворяют нормальным уравнениям. Следовательно, использование моделей авторегрессии эквивалентно линейному прогнозированию. Второй способ заключается в том, что при гауссовском приближении бесконечное продолжение корреляционной функции по ее значениям, обусловленное моделью авторегрессии, максимизирует энтропию соответствующих временных рядов. Другими словами, среди всех возможных продолжений временные ряды, соответствующие модели авторегрессии, являются наиболее "выбеленными" и имеют самый "плоский" спектр. Таким образом, метод авторегрессии эквивалентен очень популярному в настоящее время методу максимума энтропии [12,13]. 3.3.2. Метод максимума энтропии N Этот метод, впервые предложенный в работе [12], основан на предположении о том, что корреляционная функция экстраполирована так, что энтропия данных, характеризуемых этой функцией, максимальна. Эвристическое объяснение выбора такого критерия состоит в том, что он максимизирует случайность или "белизну" процесса. Энтропия определяется как Н = In [P{w)] dw, где P(t0)= £ r(«)e-i*". Для того чтобы найти максимум Я, возьмем производную от Я по {г (0, \г =N+1, N+ 2,...}. Это приведет к уравнению -- dw = 0 для\т\ = N + 1, N + 2, которое означает, что Р~х (to) определяется рядом Фурье с конечным числом членов, т. е. Р 1И= £ Т(т)е I-.(3.12) Учитывая неотрицательность Р~1 (со), в соответствии с теоремой факторизации спектра получаем £ Т(т)ет" = j- £ «(m)e4"m £ a(m)e~>m(3.13) m = - рт - 0m ~ О при некоторых \а (т) } [где а (0) = 1 и. К - коэффициент]. Другими словами, объединение (3.12) и (3.13) дает К Pico) = -rvT"7!-" • 0 ... 4 5 6 7 8 9 10 ... 78 |












