Раздел: Документация
0 1 2 3 4 5 ... 78 ного фильтра. Поэтому не удивительно, что фирма Texas Instruments выбрала для использования именно эту структуру при создании своих кристаллов синтезатора речи, имеющих большой успех [60]: модульная структура, локальные соединения, ритмичный поток данных - все это сделало удобным реализацию данного фильтра в виде СБИС [27 - 30, 39]. 1.2.1. Методы реализации алгоритма CORDIC Для реализации каждого блока на рис. 1.2,а необходимы две операции умножения и две - сложения. Поскольку операции умножения являются более дорогостоящими, были осуществлены дополнительные преобразования, чтобы ограничиться одной операцией умножения (см., например, [1.38, разд. 5.5]). По причинам вычислительного характера часто приходят к блоку с четырьмя умножителями, как это изображено на рис. 1.2, б. Однако оказывается, что этот блок в действительности может быть реализован вовсе без операций умножения. Чтобы показать это, вначале заметим, что при условии Л < 1 типичный блок решетчатого фильтра в нормализованном виде (см. рис. 1.2,6") можно характеризовать матрицей (1.5а) Причиной для такого названия является свойство 0J0*=J, J= ]Q ° »(1.56) где * - знак комплексного сопряжения. Это свойство означает, что матрица 0 сохраняет "длину" любого вектора и*= [ufuf], на который она воздействует, при условии, что длина измеряется в метрике J, т. е. 1ви2 = и2, u!2= Ul!2-u22. Матрицу 0 часто называют J-ортогональной, а результат ее умножения на вектор - J-вращением или гиперболическим вращением в противоположность обычному круговому вращению. Как указывается в [31], Д. Волдер еще в 1969 г. [58] предложил простые схемы для осуществления вращений с помощью так называемых "координатных цифровых вычислителей", или CORDIC1. В этих схемах используются только регистры, элементы сдвигов и сумматоры для итеративного расчета таких функций, как \Jx2 +у2~, a rctg (>•/*), \/х2 -у2, arctb (у/х), х cos а -- у sin а и т. д.; подобные схемы были использованы для этих целей во многих микрокалькуляторах, например в НР-35 [11, 54, 59]. 1 CORDIC - Coordinate Rotation Digital Computer. - Прим. перев. 16 В последние годы по алгоритму CORDIC строились различные одно- и двумерные вычислительные структуры систолического и волнового матричного типов на СБИС (см.. например, [2, 46, 47], а также гл. 15, 16 этой книги). Автор работ [14,15] был одним из первых, кто привлек внимание к принципу CORDIC для обработки сигналов по алгоритмам типа БПФ, а недавно в работе [20] было приведено описание СБИС, реализующей алгоритм CORDIC для арифметических вычислений. Следует отметить, что до того, как приступить к действительной реализации этого принципа (а также других схем вычислений, как, например, схем матричных умножителей), следует рассмотреть ряд факторов, таких как быстродействие, точность и др. Хочется подчеркнуть, что рассмотрение специальной математической структуры решетчатого блока позволяет построить новый макроблок для обработки сигналов. 1.2.2. Параллельные вычисления и алгоритм Шура Естественный вопрос, который возникает при использовании технологии СБИС, насколько можно ускорить процесс вычисления коэффициентов {&,-}, применяя параллельные вычисления, скажем, с помощью Л7 процессоров, работающих совместно. Надежда на успех состоит в том, что если одному процессору требуется некоторый отрезок времени на каждую элементарную операцию вычисления, то, применяя N процессоров, можно рассчитывать на получение ответа через период времени OUV), а не 0(N2), как в случае одного процессора. Однако нетрудно заметить, что длительность параллельной реализации алгоритма Левинсона составит О (Лlog Л7) из-за наличия операций вычисления скалярного произведения, необходимых для формирования последовательности А:г- ]; Лпроцессоров могут выполнять Лопераций умножения, необходимых для формирования kN+i последовательностей параллельно в единицу времени, но необходимые при этом операции сложения потребуют по меньшей мере log Af шагов. Это кажется обескураживающим, но вселяет надежду на успех. Оказывается, что существует математически эквивалентный алгоритм, предложенный Шуром [55], который позволяет избежать вычислений скалярных произведений при формировании [к{} и тем самым обеспечить с помощью процессоров вычисления за период времени 0(N). Алгоритм Шура был впервые предложен в 1917 г. в качестве теста для определения того, является ли степенной ряд аналитическим и ограниченным в круге единичного радиуса. В нашем случае он приводит к простой трехша-говой процедуре [17, 35] расчета последовательности {&,-}, связанной с ковариационной последовательностью {Rc, /?,,..., RN},R0 = 1. 1. Начнем с порождающей матрицы (символ * означает операцию транспонирования) r*JR° Ri " Rn °~ о R, -RN 17 сдвинем первую строку G* вправо для того, чтобы получить G? = It* - RN О R0 О -Rt 2.Вычислим кх по формуле &i = { } 2 2/ { Gi } 2 i • 3.Сформируем матрицу 1 1 kt 1 и получим новую порождающую матрицу О х х • • х в(А,)СТ О О где х - элементы, точное значение которых в данный момент несущественно; © известна как матрица J-вращения, поскольку О в(к)]в*(к) = J, J -С 1 Ее роль состоит во вращении в /-метрике (т.е. в гиперболической метрике) второй строки матрицы G для того, чтобы она расположилась вдоль первого координатного направления. Затем шаги 1, 2 и 3 могут быть повторены для получения значения к2 и новой порождающей матрицы G2 и т. д. Можно показать, что [к{ \, рассчитанные по алгоритму Шура, имеют точно такие же значения, что и при расчете по алгоритму Левинсона. Заметим, однако, что алгоритм Шура требует выполнения последовательности умножений вектора-строки размера 2X1 на матрицу размера 2X2, которые могут быть выполнены параллельно на каждом этапе. Поэтому для реализации алгоритма Шура с помощью N процессоров требуется период времени 0(N), а не О(/Vlog А), как при выполнении алгоритма Левинсона. В действительности параллельная поточная вычислительная структура на СБИС, основанная на алгоритме Шура, уже разработана и создана (см. [29] и гл. 17 этой книги). 1.2.3. Разложение Холецкого Алгоритм Шура тесно связан с разложением Холецкого ковариационной матрицы R в (1.1). Такое разложение применимо во многих вычислениях, связанных со стохастическими процессами. Множителем Холецкого С матрицы R называется единственная нижняя треугольная матрица с положительными диагональными элементами, удовлетворяющая соотношению R=CC*. Матрица С непосредственно определяется алгоритмом Шура: г-й столбец С = первому столбцу Gr-,(1.6) где {С/} - приведенные порождающие матрицы, полученные с помощью алгоритма Шура. 18 Таким образом, в случае разложения Холецкого для теплицевых матриц имеется быстрый алгоритм, согласно которому выполняется Q(N2) операций вместо О (А3) в общем случае. Следует упомянуть, что процедура Шура для быстрого разложения Холецкого теплицевых матриц много раз переоткрывалась в различных контекстах. Так, в [3,40, 50, 51] был, по существу, вновь найден алгоритм Шура при решении обратной задачи теории рассеяния в слоистой модели Земли. В технике алгоритм Шура был, по-видимому, впервые использован Девильдом (Dewilde) в начале 70-х гг. при решении задачи синтеза функции полных сопротивлений пассивных систем. Его приложение к задачам статистического оценивания было впервые описано в [17] ив дальнейшем использовано в [16, 33-35]; применение в теории цифровых фильтров опубликовано в [13] (см. гл. 15 этой книги, а также [46,47]). Новые структуры,полученные в этих работах, по-видимому, являются лучшими претендентами для реализации в виде СБИС. 1.2.4. Интерпретация в виде длинной линии и обратные задачи теории рассеяния Хорошей иллюстрацией естественной связи между алгоритмом Шура и его реализацией в виде СБИС (или другими методами) служит графическое представление этого алгоритма, изображенное на рис. 1.4. В этом случае полученная ранее связь между матрицами С и {G,} означает, что элементы г-го столбца представляют собой множитель Холецкого С. Следовательно, можно сказать, что данные на входах элементов задержки в любой момент времени I суть элементы /-й строки множителя С. Между прочим, такая интерпретация в значительной мере снимает налет таинственности, которая иногда связана с быстрыми алгоритмами Холецкого для строк и столбцов. Интерпретацией в виде длинной линии предполагается, что расчеты могут быть выполнены путем возбуждения структур, подобных приведенным на
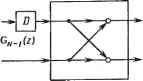 в(к,) а) в(к2) б) Рис. 1.4. Формы представления алгоритма Шура: с - прямая форма; б - модель в виде длинной линии в(к„)
рис. 1.4, с помощью световых или других электромагнитных волн в зависимости от среды, выбранной для реализации. Отметим, что, используя графические представления рис. 1.4 и фундаментальные законы распространения волн и сохранения энергии, можно получить простые доказательства всех предыдущих результатов и постепенно выяснить топкие и полезные связи между теорией длинных линий, разложением Холецкого (прямым и обратным), обратными задачами теории рассеяния и алгоритмами Шура [6]. Подобное представление в вице длинной линии оказалось также полезным при получении некоторых ортогональных каскадных схем реализации БИХ-фильтров1 с прекрасными характеристиками f46,47]. С другой стороны, к тем же результатам можно прийти, используя совершенно иной подход, если заметить, что разложение Холецкого есть не что иное, как метод проверки матрицы на положительную определенность; если теперь спросить, какие матричные структуры легко поддаются такой проверке, то придем к классу матриц, в котором семейство теплицевых матриц представляет только один частный случай [35]. При таком подходе все ранее упомянутые результаты по параллельным вычислениям и интерпретации в виде длинных линий, а также их реализации можно распространить иа значительно более широкий крут задач, что и рассмотрим кратко в разд. 1.3. 1.2.5. Алгоритмы удвоения Последний интересный результат, о котором здесь стоит упомянуть, состоит в том, что алгоритм Шура может лежать в основе получения самой простой формы алгоритма "удвоения" (или алгоритма "разделяй и властвуй") для расчета последовательности ) и для решения уравнений Юла Уокера. Применяя алгоритмы быстрой свертки для объединения импульсных откликов пар соседних 6-секций на рис. 1.4, количество вычислительных операций можно свести к l2Nlog2N [42,43] (точка пересечения данной зависимости с аналогичной зависимостью для прямого алгоритма Шура при решении теплицевых уравнений соответствует значению А= 128). Результаты, подобные OrNlog2N), были впервые получены в работах [4, 5, 41], однако в действительности алгоритмы были довольно сложными и, например, в работе [56] было подсчитано, что для метода Битмида (Bitmead) и Андерсона коэффициент при членах N\og2N равен 7000! Алгоритм, основанный на процедуре Шура, не только дает меньший коэффициент, но также более пригоден для потенциальной реализации в виде СБИС. 1.3. РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ РАЗД. 1.2 НА МАТРИЦЫ. БЛИЗКИЕ К ТЕПЛИЦЕВЫМ В начале разд. 1.2 отмечалось, чти обычным методом подгонки авторегрессионных моделей к временным рядам является решение линейных уравнений Юла-Уокера с теплицевой матрицей коэффициентов. Было упомяну- 1 БИХ-фильтр - фильтр с импульсной характеристикой бесконечной длительности. -Прим. перев. то, что зто не обязательно единственный или наилучший путь решения проблемы; сейчас поясним почему. Кратко проблема состоит в следующем: дана последовательность результатов наблюдений {у0,. .. ,ут) ; необходимо выбрать набор коэффициентов {gi ,..., а„ } так, чтобы X еп. i = minimum, (1.7) где еп i - ошибка (остаток при попытке предсказать yt по п предыдущим значениям): (1.8) е„,г = У, + Oitt-i + • + anyt-n Трудности возникают при 0<г <«, так как в этом случае нет всех п предыдущих значений. Один из выходов состоит в расчете остатков только для г>и. но по ряду причин (некоторые из которых сейчас станут понятными) мы часто рассматриваем случай t<n, полагая, что отсутствующие значения { У- „> У-n+i • • > У-i] Равны нулю. Одна из причин - предположение о том, что при Т>п произвольность такого начального допущения не скажется сильно на результатах решения в целом. Это вполне разумно, но иногда можно сделать более кардинальное допущение: расчеты вести только для 7 <г < <Т+п. полагая, что последующие значения {ут+,, . . . , Уг+п } также Равны нулю. Далее покажем, какие для этого есть основания, но вначале запишем последовательность остатков в матричной форме: (1.9) Ya, где е7* = [ев. о «„, а= [1 о, Уо УхУг уп•• у, Ут-1 Уо Уг-я Ут « Ут Наименьшее среднее квадратическое решение а, которое минимизирует е2, может быть теперь вычислено как решение "нормальных"уравнений: rY7Y]a=[R„c 0 •• О]7,(1.10) где Rft = mine[2. Теперь можно провести один из доводов для продолжения функции {е„ , по обе стороны данной выборки {у0,... ,у?} Только в этом случае матрица коэффициентов YTY будет теплицевой и, в частности, 21 0 1 2 3 4 5 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












