Раздел: Документация

0 1 2 3 4 5 6 ... 78

ковариационной матрицей выборок, использованной в уравнениях Юла- Уолкера в разд. 1.2.

Можно, однако, возразить, что вообще нет необходимости принимать какие-либо допущения относительно несуществующих данных, и поэтому использовать лишь остатки {e,v....., ellT } или, быть может, основываясь

на допущениях только относительно прошлых данных, использовать {еп0,...

еп,Т S В любом случае матрица Y7Y уже не будет теплицевой, и поэтому окажется, что "изящные" результаты разд. 1.2 по уменьшению сложности вычислений до 0(Д2) или 0(N\og2 TV) при наличии нескольких процессоров, а также при реализации решетчатых фильтров и интерпретации в виде длинных линий больше непригодны.

Это было бы весьма грустно, если бы более детальное рассмотрение не показало, что дело можно в значительной степени исправить, введя понятие "смещения" матрицы [23 - 25], которое, как будет показано, определит естественное семейство структур ковариационных матриц, обеспечивающих быстрое разложение Холецкого [35].

Не будем излагать здесь изящную и всеобъемлющую теорию, которая была разработана. Ее детальное рассмотрение можно найти в уже упомянутой работе [35] и в работах [8,12, 31, 33, 36,42,44].

Тем не менее будет полезным привести некоторые основные положения. Определим "нижнюю матрицу сдвига" как

Z-матрицу с единицами на первой поддиагонали и нулями в остальной части. С помощью Z определим смещение R формулой

смещение R-= R - ZRZr.(1-11)

Причина такого названия состоит в том, что, за исключением границ, элемент О",/) матрицы R ZRZ7 есть [R{ у- К,- у , ]. Когда R - теплицева матрица, только первые строка и столбец матрицы R-ZRZr будут ненулевыми. Определим ранг смещения R как

ранг {r ZRZ7} =cy(1.12а)

и инерцию смещения R как

инерция {R-ZRZ7} = {l,-j},(1.126)

где J - диагональная матрица с членами +1 или -1. Для теплицевой матрицы а-2 и J = 1. Матрицы YrY, которые появились в уравнениях в начале этого раздела, имели [а = 1, J = 0} при остатках [еп 0, . . ., еп т] и {а = 3, J = = диагпри остатках {еп/1,. . . ,епТ] .

1.3.1. Обобщенные стационарные решетчатые секции

Для матриц с рангом смещения а и инерцией смещения XI, - J} можно осуществить каскадную реализацию в виде общих решетчатых секций, но каждая секция будет определяться (а-1)-мерным вектором-строкой К (а не скалярной величиной, см. рис. 1.5), удовлетворяющим условию

I - KJK* > 0.(1.13)

Рис. 1.5. Обобщенная решетчатая секция

(1-KJK*)

/г

О

4

D		{3-К*КГ/г

Величины -[/С,-} могут быть найдены с помощью обобщенного алгоритма Шура. Видно, что основная стоимость аппаратурной реализации связана с наличием а-1 элементов задержки вместо одного элемента, как в теплицевом случае; однако это не очень высокая цена при современном уровне технологии, особенно если мы сохраним достоинства регулярных структур с локальными связями.

1.3.2. Нестационарные решетчатые секции

По-другому реализовать решетчатую структуру можно с помощью обычной двухлинейной решетки, но с изменяемыми во времени коэффициентами отражения. Действительно, можно показать [23], что такая решетчатая структура может быть использована для любого нестационарного процесса. Однако, применяя структуру со смещением, можно получить простые корректирующие формулы для определения коэффициентов отражения с помощью только О (а) элементарных вычислительных операций на каждом шаге. Для /операций и N коэффициентов отражения это потребует 0(ГРа) операций вычисления, а не 0(N3) , как в общем случае.

Кратко остановимся на этих формулах. Коэффициент отражения и-й секции удовлетворяет соотношению

кя+1., = {1-чя.,ч1,)1,2кя+1., 1(1-/1,,., yul, ,У12+ tl„,,ul, (1.14) где ту, /(] «-мерные векторы-строки, подчиняющиеся рекуррентным соотношениям

»7n + i,i = F{ln,t> K+i.t, M„,t~i},(1.14а)

а функция F ( •) определяется как

F{A, В, С} = (1 - ВВТУ112(А - ВСТП - ССТ)Т2-Эти рекуррентные соотношения могут быть представлены так, как изображено на рис. 1.6.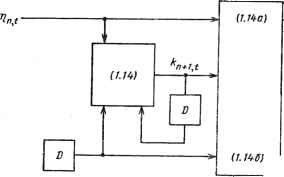

---

Рис. 1.6. Представление временной корректировки

В частных случаях эти общие результаты могут быть существенно упрощены [36]. Например1, значения г\п и с точностью до масштабного коэффициента выбираются равными "начальному" остатку \зnt с нормированной дисперсией или имеющему соответствующую задержку конечному" остатку rnt v На рис. 1.6 величины r)n>t и p.nt - сигналы, передаваемые по линиям, соединяющим элементы решетки.

В этом случае сам решетчатый фильтр может быть использован для адаптации коэффициентов отражения. Расчеты дают следующий результат-

где фи,г-1 ~~ величина, лежащая между 0 и 1. Эта величина имеет некоторую полезную статистическую интерпретацию (например, как логарифм отношения правдоподобия), которая была использована при решении специальных прикладных задач [32]. Мы упомянули об этом, так как формула (1.14) для кп+1 с Ф„? ] = 1 была первоначально получена многими авторами для так называемого приближенного адаптивного решетчатого фильтра, известного также как фильтр Итакуры -Саито, или градиентного решетчатого фильтра. Удивительно, приятно и важно, что имеется такая "изящная" форма (1.15) для точного решения, точного в том смысле, что минимизируется сумма квадратов остатков для каждого значения /; ее важность следует из того, что при точных решениях оценки по методу наименьших квадратов обладают свойствами состоятельности, несмещенности, быстрой сходимости и т.п. Поэтому данные и аналогичные им алгоритмы, такие как алгоритмы трансверсальной фильтрации фиксированного порядка, были использованы в задачах сопровождения сигнала, компенсации искажений в каналах, подавления отраженных сигналов и др. [8, 9, 10, 21, 48, 49, 53]. Специализированные СБИС, по крайней мере для одной из этих прикладных

1 В оригинале "prewindowed least-squares". - Прим, ред.

задач [19], уже разработаны, а другие, без сомнения, - в процессе проектирования.

В качестве примера другого приложения можно упомянуть архитектуру систолической процессорной матрицы для адаптивных вычислений в калма-новском фильтре [22]; зта архитектура основана на специальном методе квадратного корня для оценки состояния.

Другой областью, в которой используются идеи, подобные рассмотренным в данной главе, является вычислительная томография [7]. Системы обработки речевых, связных сигналов, изображений также являются возможными областями применения: система моделирования и распознавания голоса, кодеры-декодеры, вокодеры, системы кодирования в остаточных классах и многие другие. Приложения к радио- и звуколокации рассматриваются более подробно в последующих главах.

1.4. ЗАКЛЮЧЕНИЕ

Мы попытались рассмотреть некоторые из многих направлений, в которых могут успешно взаимодействовать, оказывая влияние друг на друга, математические достижения в алгоритмах обработки сигналов и новые возможности технологии СБИС. Такое взаимодействие приводит как к появлению новых способов физической реализации, так и к стимулированию новых теоретических достижений. Однако в этой главе был затронут только поверхностный слой, и поэтому есть много возможностей для стимулирования исследований в области обработки сигналов и методов теории систем и их применения в эпоху СБИС. Недавний отчет [47] показывает, кроме всего прочего, тесную взаимосвязь между систолическими процессорными матрицами [39] и прямыми формами цифровой фильтрации и теорией систем.

СПИСОК ЛИТЕРАТУРЫ

[1] Н. М. Ahmed, "Signal Processing Algorithms and Architectures," Ph.D. dissertation,

Department of Electrical Engineering, Stanford University, Stanford, Calif., 1982. [2] H. M. Ahmed, J. M. Deiosme, and M. Morf, "Highly Concurrent Computing Structures

for Digital Signal Processing and Matrix Arithmetic," IEEE Comput. Mag., (Feb. 1982). [3] E. H. Bareiss, "Numerical Solution of Linear Equations with Toeplitz and Vector

Toeplitz Matrices, Numer. Math., 13:404-24 (1969). [4] R. R. Bitmead, and B. D. O. Anderson, "Asymptotically Fast Solution of Toeplitz and

Related Systems of Linear Equations," J. Linear Algebra Appi, 34:103-116 (Dec. 1980). [5] R. P. Brent, F G. Gustavson, and D. Y. Y. Yun, "Fast Solution of Toeplitz Systems of

Equations and Computation of Pade Approximants," J. Algorithms, /(3):259-295

(1980).

[6] T. Kailath, A. Bruckstein and D. Morgan, "Fast Matrix Factorizations via Discrete Transmission Lines," submitted for publication, 1984.

[7] M. Buonocore, "Fast Minimum Variance Estimators for Limited Angle Computed Tomography Image Reconstruction," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., 1981.

[8] J. Cioffi, "Fast Transversal Filters for Communications Applications," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., 1984.

---

[9] J. Cioffi, and T. Kailath, "An Efficient, Exact Least-Squares Fractionally Spaced Equalizer Using Intersymbol Interpolation," IEEE Journal on Selected Areas in Communications, Special Issue on Voiceband Data Transmission, (May 1984).

[10] J. Cioffi, and T. Kailath, "Fast Recursive Least Squares Transversal Filter Algorithms for Adaptive Filtering," IEEE Trans. Acoust. Speech Signal Process., ASSP-32 (1984).

[11] D. Cochran, "Algorithms and Accuracy in the HP-35," Hewlett-Packard J., 1972, pp. 10-11.

[12] J. M. Delosme, "Algorithms and Architectures for Finite Shift-Rank Processes," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., Sept. 1982.

[13] E. Deprettere and P. Dewilde, "Orthogonal Cascade Realization of Real Multiport Digital Filters," Circuit Theory Appl, 8:245-272 (1980).

[14] A. M. Despain, "Fourier Transform Computers Using CORDIC Iterations," IEEE Trans. Comput., C-25:993-1001 (1974).

[15] A. M. Despain, "Very Fast Fourier Transform Algorithms for Hardware Implementation," IEEE Trans. Comput., C-28(5):333-341 (1979).

[16] P. Dewilde and H. Dym, "Schur Recursions, Error Formulas, and Convergence of Rational Estimators for Stationary Stochastic Processes," IEEE Trans. Inf. Theory, /Г-27(4):446-461 (1981).

[17] P. Dewilde, A. C. Vieira, and T. Kailath, "On a Generalized Szego-Levinson Realization Algorithm for Optimal Linear Predictors Based on a Network Synthesis Approach," IEEE Trans. Circuits Syst„ CAS-25(9):663-675 (1978).

[18] J. Durbin, "The Fitting of Time-Series Models," Rev. Int. Inst. Stat., 28:233-244 (1960).

[19] D. L. Duttweiler, "A Twelve-Channel Digital Echo Canceler," IEEE Trans. Commun., COM-28:647-653 (1978).

[20] G. L. Haviland and A. Tuszynski, "A CORDIC Arithmetic Processor Chip," IEEE Trans. Comput., C-29(2):68-79 (1980).

[21] W. S. Hodgkiss and J. A. Presley, "Adaptive Tracking of Multiple Sinusoids Whose Power Levels Are Widely Separated," IEEE Trans. Acoust. Speech Signal Process., ASSP-29(3)J10-72l (1981).

[22] J. M. Jover and T. Kailath, "A Parallel Architecture for Kalman Filter Measurement Update," Proc. IF AC Congress, Budapest, Hungary, July 1984.

[23] T. Kailath, "Time-Variant and Time-Invariant Lattice Filters for Nonstationary Processes," Proc. Fast Algorithms for Linear Dynamical Systems, Aussois, France, Sept. 21-25, 1981, pp. 417-464. Reprinted as Outils et modiles mathematiques pour IAutoma-tique, iAnalyse de Systemes et le Traitement du Signal, Vol. 2,1. D. Landau, ed., CNRS, France, 1982, pp. 417-464.

[24] T. Kailath, S. Y. Kung, and M. Morf, "Displacement Ranks of Matrices and Linear

Equations," J. Math. Anal. Appl., <58(2):395-407 (1979). [25] T. Kailath, S. Y. Kung, and M. Morf, "Displacement Ranks of a Matrix," Bull. Am.

Math. Soc, l(5):769-773 (1979).

[26] Т. Kailath, Lectures on Wiener and Kalman Filtering, Springer-Verlag, New York, 1981. [27] H. T. Kung, "Lets Design Algorithms for VLSI Systems," Proc. First Caltech VLSI Symp., 1979, pp. 65-90.

[28] H. T. Kung, "Why Systolic Arrays?" IEEE Computer, /5(l):37-6 (1982).

[29] S. Y. Kung and H. Hu, "A Highly Concurrent Algorithm and Pipelined Architecture for

Solving Toeplitz Systems," IEEE Trans. Acoust. Speech Signal Process., ASSP-3I(1):66-

75 (1983).

[30] S. Y. Kung, K. S. Arun, R. J. Gal-Ezer, and D. V. Bhaskar Rao, "Wavefront Array Processor: Language, Architecture and Applications," IEEE Trans. Comput., C-5/:1054-1066(1982).

[31] D. T. Lee, "Canonical Ladder Form Realizations and Fast Algorithms," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., 1980.

[32] D. T. Lee and M. Morf, "A Novel Innovations Based Approach to Pitch Detection," Proc. 1980 IEEE Int. Conf. Acoust. Speech Signal Process., Denver, Colo., Apr. 9-11, 1980, pp. 40-44.

[33] ri. Lev-Ari, "Parameterization and Modeling of Nonstationary Processes," Ph.D. dissertation, Stanford University, Stanford, Calif., 1983.

[34] H. Lev-Ari, "Modular Architectures, for Adaptive Multichannel Lattice Algorithms," IEEE Int. Conf. Acoust. Speech Signal Process., Boston, Apr. 1983, pp. 455-458.

[35] H. Lev-Ari and T. Kailath, "Lattice Filter Parametrization and Modeling of Non-stationary Processes," IEEE Trans. Inf. Theory, IT-JO, (Jan. 1984).

[36] H. Lev-Ari, T. Kailath, and J. Cioffi, "Least-Squares Adaptive Lattice and Transversal Filter for Nonstationary Processes," IEEE Trans. Inform. Theory, IT-30, (Mar. 1984).

[37] N. Levinson, "The Wiener RMS (Root-Mean-Square) Error Criterion in Filter Design and Prediction," J. Math. Phys., 25(4):261-278 (1947).

[38] J. Markel and A. H. Gray, Jr., Linear Prediction of Speech, Springer-Verlag, New York, 1976.

[39] C. Mead and L. Conway, Introduction to VLSI Systems, Addison-Wesley, Reading, Mass., 1980.

[40] M. Morf, "Fast Algorithms for Multivariable Systems," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., 1974.

[41] M. Morf, "Doubling Algorithms for Toeplitz and Related Equations," Proc. IEEE Int. Conf. Acoust. Speech Signal Processing, Denver, Colo., Apr. 9 11,1980, pp. 954-959.

[42] D. R. Morgan, "Orthogonal Triangularization Methods for Fast Estimation Algorithms," Ph.D. dissertation, Department of Electrical Engineering, Stanford University, Stanford, Calif., Dec. 1984.

[43] B. Musicus, •Levinson and Fast Cholesky Algorithms for Toeplitz and Almost Toeplitz Matrices," MIT Internal Report, submitted for publication, 1981.

[44] B. Porat, "Contributions to the Theory and Applications of Lattice Filters," Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, Stanford, Calif., 1982.

[45] L. R. Rabiner and R. W. Schafer, Digital Processing of Speech Signals, Prentice-Han, Englewood Cliffs, N. J., 1978.

[46] S. K. Rao and T. Kailath, "Orthogonal Digital Filters for VLSI Implementation," IEEE Trans. Circuits Systems, CAS-3I, (1984).

[47] S. K. Rao and T. Kailath, "Digital Filtering in VLSI," Technical Report ISL, Stanford Univ., Stanford, Calif., Jan. 1984.

[48] V. U. Reddy, B. Egardt, and T. Kailath," Optimized Lattice-Form Adaptive Line Enhancer for a Sinusoidal Signal in Broadband Noise," IEEE Trans. Circuits Sysr., CAS-28:542-550 (June 1981).

[49] V. U. Reddy, T. J. Shan, and T. Kailath, "Application of Modified Least-Squares Algorithms to Adaptive Echo Cancellation," Proc. 1983 Int. Conf. Acoust. Speech Signal Process., Boston, 1983, pp. 53-56.

[50] J. Rissanen, "Algorithms for Triangular Decomposition of Block Hankel and Toeplitz Matrices," Math. Сотр., 27:147-154(1973).

0 1 2 3 4 5 6 ... 78