Раздел: Документация
0 ... 43 44 45 46 47 48 49 ... 78 Sz. Множитель Множимое Шина считывания t Шина считывания 2 V Сумматор Знак Триггеры знак х Знак У Шина записи Vf Сйых Sn-rSn- Синхрони-зация и \ управление Рис. 16.6. Косвенный умножитель и множимого, а также «-разрядный накопитель А, в котором хранятся частные суммы. Два триггера содержат знаки операндов. Обозначим-г-й бит числа Y через Yt, и пусть К Y, = 0 представляет собой «-разрядный результат иХ1 логической операции И. Произведение XY вычисляется по следующему алгоритму: For i = 0 to n - 1 begin; Свых - S *- A + (X Л Y0)/*споженив*1 A.YCte. S . Y„ , Y„ 2 ... Yi + I I*cd8u: end;1 + 1 где S и Свых - сумма и цифра переноса на выходе из сумматора; А.В -конкатенация 4иВ. В конце операции умножения в регистре A. Y появляются 2и-разрядные произведения. Заметим, что сдвиг вправо в указанном алгоритме совершенно аналогичен сдвигу влево в искомом методе. В этой схеме косвенного умножения на одну операцию умножения требуется п циклов. Например, если операции умножения над 16-разрядными сомножителями длятся 500 не, то время каждого цикла равно 31 не. Длительность каждого цикла определяется временем доступа к регистрам, вре- менем выполнения сложения и сдвига и, наконец, запоминания результата в А и X регистрах. Скорость умножения, необходимая для достижения заданного времени, в значительной степени зависит от числа используемых Щин; их наименьшее число равно трем (рис. 16.6), при этом два суммируемых операнда одновременно выбираются отдельными шинами, а для записи результата необходима еще одна. Можно ускорить выполнение сдвига и сложения, если в одном цикле оперировать с несколькими разрядами, а не с одним. Эта схема известна как схема умножения с просмотром разрядов. Рассмотрим «-разрядные величины, разделенные на неповторяющиеся fc-разрядные блоки. Без ограничения общности будем считать п целым, кратным числу к. Пусть тя,- - значение 1-го блока. Тогда алгоритм умножения может быть записан как for i = 0 to (n/k) - 1 begin; Омг. S.-A + m,X A.Y <- C&/x. S . Yn i Y„ 2 • • • Yi+k end; где теперь вправо сдвигается к разрядов вместо одного. Заметим, что т}Х = к£Ьи2% 1 = 0 где bk y-fefc 2 / - • • 0 / ~ блок из к разрядов. Поэтому произведение nijX легко выполняется сложением к + 1 операндов. Для этого только требуются составные сомножители, которые легко получаются путем сдвига. Так как в операциях используются к разрядов сразу, эта схема требует только [п/к] +1 циклов на полное умножение, что меньше,чем п, однако за счет усложнения оборудования. Примечательно, что метод умножения сканированием эквивалентен умножению по основанию г = 2к. Мы видели, что каждый разряд в таком умножителе с просмотром разрядов вносит вклад в частичное произведение. Число операций сложения можно уменьшить, используя некоторые свойства разрядных строк. Время выполнения уменьшим путем сдвига длинных нулевых строк в умножителе. Например, рассмотрим строку, включающую в себя к последовательных единиц: ...0, 1, 1, 1,..., 1,0. . . к Используя тот факт, что 2i +k-2i =2i +k-l+2i + к - 2 + .. . + 2i +1+2/ строку можно перекодировать как ... 1,0,0, ...,0, 1,0 "~кТ где 1 используется для обозначения -1. Теперь к последовательно выполняемых операций сложения благодаря перекодированному множителю заменяются единственной операцией сложения и единственной операцией умножения. Именно зто свойство является полезным в перекодированных операциях умножения (см., например, [17 - 19]). 16.4.2. Умножители с перекодированием Только что продемонстрирован простой способ перекодирования строки разрядов, при котором уменьшается число операций сложения, требуемых при выполнении умножения. Это свойство, известное как перекодирование строк, является основой многих методов, включая знаменитый метод Бута [20]. Пусть ВР - строка из п двоичных символов и пусть D - перекодированная строка, состоящая из п символов, выбранных из алфавита {1, 0,1 } . Тогда если В = 0 • В • 0, то 0,В, = «, ( 1, К, <«,-,, 1,B,>B-i, где Dj - i-й символ строки D. Ясно, что перекодирование всей строки может быть выполнено очень быстро путем параллельного перекодирования всех разрядов. Целью перекодирования является получение строки D, содержащей больше нулевых символов, чем строка В (напомним, что эта операция не входит в умножение), и тем самым повышение скорости умножителя. В общем случае перекодирование эффективно для строк В, не содержащих много изолированных единиц. Алгоритм умножения Бута может быть представлен в следующем виде: for end; = 0 to n - 1 begin; f Y0 = Y, then PP <- right shift (PP) f Y, < Y0 then PP <- right shift (PP + X) f Y, > Y0 then PP - right shift (PP - X) где PP является частным произведением, хранимым в A. Y. Согласно этому алгоритму числа обрабатываются непосредственно в дополнительном коде без преобразования в форму со знаковым разрядом. 16.4.3. Матричные умножители - умножитель Брауна Рассмотрим два положительных целых числа А=ап 1, ап 2 -°о и В = = Ът \Ът 2 1>о,имеющих значения т 1 А= £а,2\ В= ХМ. i=0=0 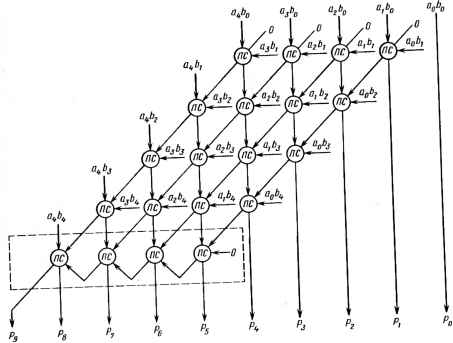 Рис. 16.7. Умножитель Брауна: ПС - полный сумматор Необходимо получить произведение m - 1 п iи+в-1 Р = АВ= I 2>,A)2+J= I П2". 1 = 0 1 = 0*=0 Последнее равенство обладает интересным свойством, состоящим в том, что каждое значение./ является суммой одноразрядных результатов afij, каждый из которых может быть получен операцией И. Схема матричного умножителя для т = 5 и и = 4 показана на рис. 16.7. Это устройство, известное как умножитель Брауна [21], построено из совокупности ячеек полных сумматоров (ПС), на входы которых подаются одноразрядные произведения atbj. Структура такого умножителя является совершенно регулярной и полностью пригодна для интегрального исполнения, так как состоит из т(п - 1) одинаковых одноразрядных сумматоров, а также изт-и вентилей И. Производительность матрицы можно оценить, анализируя наиболее длинный путь прохождения данных. Время умножения определяется формулой Т=Та + («+ш-2)7у, где Та и 7у - задержка времени распространения в элементе И и одноразрядном сумматоре соответственно. Выбирая и-канальную МОП-технологию и используя вентили с одинаковым управлением, имеем Tf = 2Ta, что дает Т= (2п+2т-3)Та. Таким образом, умножитель 16X16 разрядных слов, выполняющий умножение за 500 не, требует задержки на вентиль 8 не. Если учесть, что каждый выход одноразрядного сумматора соединяется только с двумя идентичными элементами, расположенными в непосредственной близости на кристалле, то требования к производительности оказываются более реальными, чем длительность цикла, равная 31 не для косвенного умножителя, рассмотренного ранее. При тщательном исследовании производительности этого умножителя ясно видно, что задержка {тп - 1)7у получается в нижней строке сумматоров из-за распространения цифры переноса. Эта задержка может быть уменьшена до некоторого постоянного значения (например, 10Ta) путем выполнения операции суммирования с предварительным просмотром цифры переноса ,в нижней строке сумматоров. С учетом этого время умножения Т= (2п + 10)То. Таким образом, 500-нс умножитель может быть реализован с задержкой 12 не на вентиль при введении дополнительной аппаратуры для просмотра переноса. - В умножителе Брауна обрабатываются целые положительные числа, что неизбежно требует дополнительной аппаратуры, которая управляет преобразованием числа (например, в обратный или дополнительный код). Мы бы предпочли структуры, в которых обрабатываются непосредственно числа, именно такие структуры являются темой подразд. 16.4.4. 16.4.4. Умножитель Бо-Вулн, работающий с дополнительными кодами Матричные умножители, которые оперируют непосредственно с дополнительными кодами чисел, обсуждались многими авторами [22, 23]. Проиллюстрируем метод [23] (рис. 16.8) для случая тп-6, п =4. По-прежнему умножение выполняется как накопление последовательных слагаемых. Нововведением в методе Бо-Вули является то, что все слагаемые положительны, поэтому требуется только аппаратура простого сложения, несмотря на то, что операнды могут быть и отрицательными. Вновь начнем с двух двоичных векторов А=ат ат 2 - • -яо и В = = bn ibn 2 • -bib0, образующих дополнительный код числа. Их значения определяются в виде т -2и- 2 А = -am 12™-1 + X at2\ в = -Ь„ 12"~1 + £ bt2\ i=0i = 0 и их произведение Р= Fm+n 1/J„,+„ 2 • • pi {Jo имеет значение 284 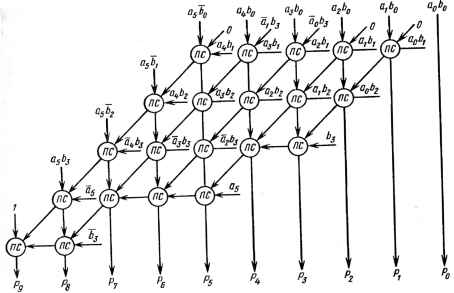 Рис. 16.8. Умножитель Бо-Вули: ПС - полный сумматор 1+И-2 Г "о р р 12т+""1 + У, P.2f = am-1b„-i2m+" 2 + т-2п-2 т-2"2... i = 0 j = 0 Две последние операции вычитания легко преобразуются в операции сложения в дополнительном коде. Решающим в данном методе является то, что число Х=х.1х 2 • • • >*i*o > значение которого определяется как *-2 Х= - хк2кх + У>,2;, i = 0 может быть проинвертировано в виде -X = -(1 - хк ,)2* 1 + 1(1 - х,)2< + 1. i = 0 Применяя это действие к записанным ранее уравнениям, можно переписать произведение в виде сумм (т.е. без вычитания) т - 2 л 2 Р = ат„1Ь12™+"-2 + £ 2>А2+ + 2т + и + 2т + я1 + (5Я 1 + i = 0 j=oL т-2 Ьи 1)2т+И"2 + b„-i + I aA-i2 + am-i + i=0 0 ... 43 44 45 46 47 48 49 ... 78 |












