Раздел: Документация
0 ... 44 45 46 47 48 49 50 ... 78 Последнее выражение, обеспечивающее получение произведения Р исключительно с помощью операций сложения, и лежит в основе умножителя Б о-Були. На рис. 16.8 показана матричная схема реализации умножителя на основе одноразрядных полных сумматоров при т=6, и = 4. В общем случае требуется матрица из т (и - 2) + 3 одноразрядных полных сумматоров, а время умножения составляет Т=2Та + (m + n)Tf = 2(m + n + l)Ta. Если тп=п, то нижняя строка матрицы упрощается и выполнение операции сложения с предварительным просмотром цифры переноса обеспечивает существенное повышение скорости. Если предварительный просмотр цифры переноса дает время сложения, равное ЮТа, то Т=2(п + 6)Та. Быстродействие вентилей и объем требуемого оборудования для выполнения этого умножителя сравнимы с таковыми в матричном умножителе Брауна, оперирующем только с положительными целыми числами. Если умножитель Брауна дополнить преобразователем в дополнительный код, имеющий задержку 2пТа, то устройство Бо-Вули окажется лучше и по быстродействию, и по полезной площади кристалла. 16.4.5. Другие стратегии умножения Два дополнительных метода умножения, которые успешно применяются в области обработки сигналов, основаны на логарифмической обработке и арифметике вычетов. В первом случае мы видим, что А В = log"1 (log„4 + log В). Поэтому при хранении значений log х и log"1 х в таблице (табличной памяти) эта схема требует только одной операции сложения и трех обращений к табличной памяти. Ограничение логарифмической обработки связано с потребностью в очень больших таблицах для достижения высокой точности, что лимитируется временем и площадью кристалла. За дальнейшей информацией читатель отсылается к работам [24, 25]. Применение арифметики остаточных классов (вычетов) в системах обработки сигналов представляет большой интерес, так как все разряды в представлении вычета имеют равный вес. Отпадает необходимость в информации о переносе (из разряда в разряд) , так как нет ни младших, ни старших разрядов и, таким образом, арифметические операции реализуются очень быстро. Например, пустьР=Р1, Рг ,Рк - множество модулей, элементы которого относительно просты. Единственное представление числа Хе [-N/2,N/2] через вычеты задается /Г-компонентным вектором X X i, X2,..., Хк t где Г X mod Рр Xj > О, [ Р( - (\Х;\ mod />,-), Х( < О; к N= X Р, . 1=1 16.5. АЛГОРИТМ CORDIC В разд. 16.4 было показано, что некоторые алгоритмы цифровой обработки лучше описываются обобщенными векторными функциями вращения, чем простым умножением. Алгоритмы координатного вращения CORDIC (coordinate rotation digital computer) обеспечивают эффективный, по существу поразрядно-рекурсивный, метод для вычисления двумерных векторных функций вращения с помощью простых операций сдвига и сложения. Для системы координат с параметром ш, в которой норма R и угол Ф вектора Х= (х0, у о) определяется в виде R = лДо + myl, Ф = т arctg Оо у/гп/хо ), итеративный алгоритм CORDIC задается как [29] 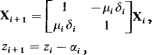 (16.1) I Х=х1хг ...хк, Y=y,y2 ...ук, обозначаемая X-Y (где "•" обозначает сложение, умножение или вычитание), выполняется просто: X-Y= (х1 -у, хг-у,...хк.ук), так как каждый разряд вычета вычисляется независимо; этот арифметический метод обеспечивает высокое быстродействие и способствует высокому параллелизму. Арифметика вычетов, тем не менее, не свободна от проблем. Например, числа ограничены динамическим диапазоном [-Л/2, Л/2], который часто меньше диапазона, допускаемого двоичным представлением. Преобразование из обычного двоичного вида в представлении через вычеты часто выполняется табличным методом, который становится фактором, ограничивающим скорость. Возможно, что наибольшим недостатком этого подхода является то, что из-за отсутствия весов разрядов алгоритмы операций, таких как деление, масштабирование, округление, сравнение по модулю, очень громоздки. Ситуации, в которых такие операции встречаются очень часто, приводят к многочисленным преобразованиям представления чисел, и преимущество арифметики вычетов теряется. Дополнительную информацию можно найти в [26 - 28]. Оба способа построения арифметического устройства для обработки сигналов (логарифмической обработки и использования арифметики вычетов) являются нестандартными. Однако из-за совокупности указанных трудностей их не используют в традиционных случаях обработки сигналов, поэтому мы не будем уделять им внимание. Читатель, интересующийся специфическими алгоритмами, может найти эти методы очень полезными; сведения о них изложены в литературе. Перейдем к рассмотрению некоторых вариантов традиционного АУ, которые хорошо подходят для общих алгоритмов обработки сигналов. X - ff-z- (m = D- z-0 x- У-z- (m=0):z-0 x У z- X У z (m=-i):z-n Kj(xcosz-ysu\zi -K,(y COSZ+XSMZ) 0 al -X y+xz -0 6} K4(xchz + yshz) - K-j(ycr\z+xsbz) -0 8} x - y- z- x- У z- (mO):y-0 x-У-z- X Y 2 (m=-t):y-/ Рис. 16.9. Функции алгоритма CORDIC: a - круговая; б - линейная; в - гиперболическая К,\/х*7у~г О z~ anl§-(y/x) - х О Z- (У/Х) -к-,/х!-уг -о -z-wctt\-(y/x) где 1г- 1 = -arctg (5- т " {&{} - множество произвольных констант. Эти уравнения определяют поворот вектора X,- на угол щйх до положения Х+1, где щ =±1 - направление вращения. Суммарный угол поворота за шаг г, при котором используется начальный вектор Х0, накапливается во вспомогательной переменной zt. Определяя начальное значение г0=в и выбирая последовательность поворотов {д/б/} , такую, что zn ->0, получаем поворот Х0 на угол в. Аналогично, устанавливая z0 = 0 и выбирая {мг-бг-} для поворота Х0 до известного значения Хп, накапливаем значение угла между векторами Х0 и Х„ в переменной zn- Например, если вектор Хи расположен вдоль абсциссы, то zn = arctg (уо/Хо), тем самым получается функция, обратная тангенсу в частной системе координат, определяемой значением т. Особый интерес представляют круговая, линейная и гиперболическая системы координат с соответствующим значением т-1, 0, -1. Относящиеся к ним функции показаны на рис. 16.9. Ключ к простому выполнению рекурсивных алгоритмов вращения лежит в выборе значений {б,-\ . Если значения {б,} являются целой степенью основания системы счисления, используемой в машине (например, бг- =2~), го масштабирование с помощью 6г- сводится к простому сдвигу и сложению.  -Знак у -Знакх Рис. 16.10. Арифметическое устроГгство CORDIC Общие указания для выбора значений {б,-} и {аг-} даны в [14, 29]. Ясно, что последовательность {а{} должна быть невозрастающей для сходимости алгоритма. Сходимость алгоритма проанализирована в [14]. Если {б;} выбраны, как предложено, то арифметическое устройство CORDIC приобретает простую форму, представленную на рис. 16.10. Каналы х и у обеспечивают преобразование X,- в Хг+1 в соответствии с уравнением (16.1), в то время как канал z накапливает углы поворота,используя значения {а,-j , получаемые из таблицы. Обычно п значений б,- и, следовательно, a.j достаточно для «-разрядных величин. Эти значения выбираются заранее и запоминаются. Все углы поворота в аппроксимируются выбором соответствующих значений {а,-} (напоминаем, чтощ=±\), поэтому и- 1 £ = 0 и уравнения алгоритма CORDIC определяют импульсную систему управления поворотом Х0 до положения Хп последовательностью предопределенных по абсолютному значению поворотов с динамически выбираемым направлением. 16.5.1. Характерные особенности метода До сих пор мы игнорировали важное свойство выражения (16.1). В действительности это выражение характеризует не только поворот от X,- до XJ+1, но и масштабирование вектора, так что Х, + 1 = К,Х,-, где К, = У1 + mef. Поэтому после п итераций имеем Х„ = КХ0, где п- 1 i = 0 Следовательно, функции, получаемые векторным вращением, масштабируются коэффициентом К, как показано на рис. 16.9. Следует найти способ нормирования с целью исключения этого коэффициента. Другая проблема алгоритмов вращения связана с их ограниченной областью сходимости. Не все возможные углы поворота в интересующей системе координат дают сходимость к желаемому результату. Выбор {бг} заметно влияет на область сходимости. В литературе приводится большое число схем, расширяющих область сходимости и исключающих масштабирование [29, 30]. Во всех из них предусмотрена проверка значения Хг- для определения необходимости корректировки и корректировка процесса дополнительными .вычислениями. Эти схемы обычно приводят к значительному уменьшению скорости вычислений [15]. Эффективный метод для одновременного расширения области сходимости нормализации был предложен в [ 14]. Он приводит к небольшим потерям в скорости вычислений, основан только на основных уравнениях алгоритма CORDIC и поэтому не требует дополнительного введения специального оборудования. 16.5.2. Применение арифметических блоков CORDIC в обработке сигналов Многие алгоритмы обработки сигналов могут быть реализованы на основе функций вращения, вычисляемых по алгоритмам CORDIC. К некоторым очевидным прикладным задачам относятся задачи комплексной арифметики, например задача дискретного преобразования Фурье или комплексной фильтрации и задачи адаптивного выравнивания при модуляции-демодуляции. При реализации алгоритмов решения этих задач, детально рассмотренных в [12, 13], используется выражение для операции комплексного умножения через операции кругового вращения. Преобразование алгоритма в операции координатного вращения не всегда очевидно, как было в примере уравнения многозвенного фильтра лестничного типа (см. разд. 16.4). Пользуясь определенным представлением, уда- ось выразить операции фильтра в виде последовательности круговых или гиперболических вращений. На рис. 16.11 показана структурная схема соответствующего АУ с нормализацией масштабирующей константы. Только два АУ и пять операций необходимы для выполнения вычислений в многозвенном фильтре лестничного типа, которые весьма громоздки при использовании умножителя традиционной структуры. 16.5.3. Повышение скорости выполнения алгоритма Мы показали, что производительность косвенного умножителя может быть значительно повышена использованием, например, матричного умножителя. Предлагаемый вариант основан на том факте, что частные суммы, требуемые при умножении, могли порождаться параллельно. К сожалению, это не так в случае с делением и операциями алгоритма CORDIC, каждая последующая итерация которых зависит от знака предыдущего результата. Следовательно, возможности для ускорения этих операций сильно ограничены. Как уже отмечалось, обработка сигналов состоит из повторяющихся операций, которые могут быть конвейеризованы. Используем этот факт для построения АУ конвейерной архитектуры, выполняющего алгоритм CORDIC (рис. 16.12). Требуемая для этого дополнительная площадь кристалла при использовании МОП-технологии невелика. Локальность связей также облегчает задачу размещения. Для параллельного сдвигового регистра в схеме на рис. 16.10 бесспорно требуется большая площадь кристалла в обычном АУ для алгоритма CORDIC. В конвейерном АУ каждый сдвиговый регистр присутствует на каждом этапе и способен выполнять один или два различных сдвига при определенном предварительном выборе {бг- $ - Следовательно, при реализации этой большой части схемы не вводится значительной избыточной площади; однако увеличивается скорость благодаря уменьшению задержки сдвигового регистра в расчете на один этап. >: Если для выполнения полной операции в обычном блоке CORDIC требуется время Т-пТс (где Тс - время одной итерации), то время ожидания /. и период Т конвейерного АУ составляют L = пТс ,Т=ТС , где Тс < Тс благодаря уменьшению задержки в сдвиговом регистре. Длинная последовательность операций вращения выполняется с фактическим периодом Тс, а не с периодом пТс. й Арифметическое устройство CORDIC также очень полезно в матричном процессоре (например, в систолической матрице) для выполнения операций матричной алгебры, которые являются общими в обработке сигналов, например разложение матрицы, что детально рассмотрено в [31, 32]. Свойства сходимости алгоритма позволяют повысить скорость неконвейерного способа реализации координатного вращения (см. рис. 16.9) согласно выражению (16.1). Ограниченный объем данной главы не позволяет изложить подробности, представленные в [14], поэтому приведем только 0 ... 44 45 46 47 48 49 50 ... 78 |












