Раздел: Документация
0 ... 45 46 47 48 49 50 51 ... 78 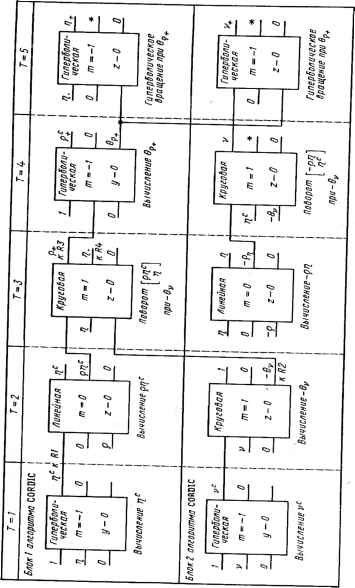 s (Г II + С с-и с-с II II В. Н а а X ж II со X I 8. ка КИ aк щн Р.га о 8р р., ft; 292 Итерация 1 Итерация 2 Итерация п Регистр\ АУ ЯеащрГН АУ
АУ Тактовые импульсы
АУ Тактовые импульсы In Рис. 16.12. Конвейерная организация блока, выполняющего алгоритм CORDIC важные результаты. Фактически получена гибридная схема, в которой наряду с обычной аппаратурой для выполнения алгоритма CORDIC используется умножитель. Во-первых, заметим, что вектор Хт определяется с помощью переменной zm из вектора за т шагов [29]. Последовательность {а{} полагается убывающей, состоящей из п углов. Рекурсивные вычисления прекращаются после т< N шагов, оставляя при этом небольшой остаточный угол поворота zm . Отбрасывая все члены ряда Тейлора в разложениях sin zm и cos zm, за исключением первых (что справедливо для достаточно малых значений zm), можно получить следующие приближенные значения: cos zm ~ 1, sin zmzm. Теперь из Хт единственным поворотом с коэффициентом zm получаем Хп в виде rcoszm -sinzm- Г1 -zl Ism z„ cos zj lzm 1 J - Следовательно, окончательное вращение получается с помощью двух операций умножения в небольшом умножителе (каждая из которых может быть заменена операцией сдвига, т. е. zm - 2"k) за время Т = тТс + 2Тт, где Тт - время выполнешя операции умножения. Главный результат, который оправдывает зту гибридную схему, состоит в том, что для и-разрядной точности отбрасывание младших членов в ряде Тейлора оправдано для [14] гп~> (п + 1)/2, гак что приблизительно половина итераций алгоритма CORDIC может быть исключена. Другие гибридные методы даны в [14]. Замечание. Поток данных в этой гибридной схеме направлен из блока координатного вращения в умножитель. Для повышения эффективности эти два устройства можно включить по конвейерной схеме, согласно которой аппаратура координатного вращения начинает следующую операцию после передачи в умножитель результата предыдущей операции. 16.6. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ Метод последовательных приближений (convergence computation method) является итеративным и применяется для вычисления некоторых элементарных функций [4]. Чтобы вычислить значение z0=f(x)\x=x , введем переменную у и функцию F (х, у), удовлетворяющую требованиям:° 1)существует такое значение у0, при котором F (х0, у0) = z0; 2)существует непрерывное преобразование (хк, ук) -> (хк+1, ук+1), такое, что функция F(хк, ук) инвариантна относительно G при всех к> 0; 3)существует значение xw, достижимое преобразованием G изх0 - Тогда результирующее значение уш, получаемое преобразованием G, удовлетворяет равенству yw = F(xw,yw) =z0, что является желаемым результатом. Например, если /(л) = wex, то, выбирая F (х, у) = уе* и у о - w, удовлетворяем условию 1. Затем выбираем преобразование хк+1 =хк ]пак>>к + 1 =>как-Ясно, что F(хк, ук) = F(xk+1, ук+1) при всех к> 0, т.е. удовлетворяется условие 2. Наконец, пусть xw = 0. Тогда Иw xw = х0 - X 1п ак~> № П ак = х0, 11 т.е. удовлетворяется условие 3, и w F(xw, vj = yw = у0 П ак, 1 что дает желаемый результат. Для простоты реализации коэффициенты ак выбираются в виде (для машин, работающих в двоичной системе) ак = 1+2тк, что приводит только к операциям сдвига и сложения при преобразовании ук. Выбор величин тк детально рассмотрен в [4]. Значение тк влияет на скорость сходимости алгоритма, который требует не меньше и/4 итераций для «-разрядной точности. Структурная схема соответствующего устройства приведена на рис. 16.13 и состоит из устройств сдвигай сложения, сое-294 X х или у т < т ,К следующему алгоритму т СдВигатепь ТU 2тх(хилцу) Сумматор сверхоперативная память C(m)=-\f\(J+2-°°) M С(т) Рис. 16.13. Арифметическое устройство для вычислений методом последовательных приближений диненных с табличной памятью небольшой емкости для хранения значений а. Следует обратить внимание на сходство с методом CORDIC, согласно которому значения {бг-} выбирались в соответствии с основанием системы счисления, а таблица требовалась для хранения значений {аг-}. 16.7. СРАВНЕНИЕ АРИФМЕТИЧЕСКИХ УСТРОЙСТВ Мы представили несколько примеров арифметических устройств и некоторые алгоритмы, для выполнения которых они предназначены. Теперь приведем результаты сравнения этих структур, а также их производительности. Все операнды предполагаются «-разрядными. Следует, однако, предупредить, что результат сравнения может часто изменяться в зависимости от принятых допущений. Вначале рассмотрим полезную площадь кристалла при использовании каждого устройства в виде СБИС. Относительные площади кристаллов приведены в табл. 16.1, где в качестве основы для сравнения используется косвенный одноразрядный умножитель. Его схема согласно рис. 16.6 состоит из «-разрядного сумматора, трех регистров и двух триггеров. Для выполнения преобразования в дополнительный код в эту схему следует ввести соответствующий преобразователь, который более легко реализуется в ви- Таблица 16.1. Относительная площадь кристалла, требуемая для реализации различна арифметических устройств. Все операнды «-разрядные
де преобразователя в обратный код с добавлением сумматора для младшего разряда. Мы предположим, что площадь одноразрядного сумматора с его шинами эквивалентна площади трех ячеек памяти с их шинами. Это предположение справедливо для п МОП-технологии. Размеры параллельного сдвигового регистра, требуемого в арифметическом устройстве CORDIC, получены из [14, 30] после соответствующего пересчета площади с целью сравнения с остальной частью АУ, выполненного по идентичной технологии. Был проведен эквивалентный пересчет и площади разводки для матричного умножителя, длина линий связи которого невелика. Все схемы реализации основаны на параллельной поразрядной арифметике; заметим, что параллельное АУ для выполнения алгоритма CORDIC вычисляет все три уравнения координатного вращения параллельно, в то время как последовательные АУ выполняют эти вычисления последовательно. Необходимо отметить, что относительные площади кристаллов конвейерного АУ и параллельного АУ растут линейно с ростом и. Можно было ожидать, что относительная площадь кристалла конвейерных устройств растет как и2; тем не менее этого не происходит, так как пространство, отведенное под регистр сдвига, не растет с ростом п. (Необходимо отметить, что в этих схемах пропорционально п2 растет абсолютная, а не относительная площадь кристалла.) Наконец, в Таблица 16.2. Относительная скорость работы арифметических устройств. Все операнды разрядные Тип умножителяТ1 Т2Т1 Т2Т1 Т2Tl Т2 умножение вычислениевычислениевычисление тригономет-угла поворо-ч/х2 + >2 рической та вектора функции
* Предполагается составной метод последовательных приближений. I - --- рассмотрение не включены умножители на основе логарифмической обработки и на основе остаточных классов (вычетов), так как площадь кристалла для них определяется памятью. В значениях относительной площади, приведенных в табл. 16.1, не учтена площадь схемы управления последовательной работой АУ (например, итерациями последовательного умножителя или операциями алгоритма CORDIC); эта площадь примерно одна и та же для различных стратегий. Как видно, площади арифметических устройств алгоритма CORDIC или метода последовательных приближений оказываются меньше, чем площади матричных умножителей. Они обеспечивают выполнение широкого набора функций, но со значительно меньшей скоростью. Относительные скорости 77 работы различных АУ для операндов разрядностью п приведены в табл. 16.2. Это сравнение основано на том, что доступ к регистру возмо- 297 0 ... 45 46 47 48 49 50 51 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












