Раздел: Документация
0 ... 60 61 62 63 64 65 66 ... 78 Р. Шрайбер, Ф. Кьюкес1 22.1. ВВЕДЕНИЕ Ряд недавних публикаций в литературе по обработке сигналов, архитектуре ЭВМ и проектированию СБИС показали чрезвычайную полезность использования систолических структур при разработке специализированных высокопроизводительных приборов для реализации численных методов линейной алгебры [1,5]. Однако в них не было уделено внимания проблеме интеграции этих разработок в какой-либо вычислительной среде или системе обработки сигналов. Целью данной главы является рассмотрение конкретного варианта применения систолических матриц, а именно для решения проблемы адаптивного формирования луча. Эта проблема проста и в то же время типична для обработки акустических сигналов. Сигналы принимаются антенной решеткой, состоящей из т идентичных датчиков, запоминаются и подвергаются преобразованию Фурье по времени. Результатом этих преобразований является множество комплексных величин л: (со, /), зависящих от частоты (cj) и номера датчика (/). Затем для каждой из результирующих частот должен быть получен массив значений выходных функций, зависящих от угловой координаты: m g((o9 9) = X x(w> Oft со, 9), i = 1 где w - комплексно-сопряженная величина. Вектор w определяет характеристики формирователя луча. Для формирователя с минимальной дисперсией неискаженного отклика w выбирается по критерию минимизации выходной мощности при ограничении m X Ф, со, 9)Щ9 со, 9)= 1, где c(i, со, #) - выходной сигнал датчика i на частоте со, обусловленный входным сигналом только от источника с угловой координатой Ъ. Решением является весовой вектор w(co, 9) ее (w(l, со, 9\ ..., w(m, со, 9))т вида w=Rc/(c*Rc), где с - вектор полезного сигнала; Rxx - ковариационная матрица сигнала на частоте со: Rxx(co) = £{х(со)х*(со)}. 1 Фирма ESL, Саннивэйл, Калифорния. 382 На практике для каждой из частот получается (иХга) -матрица отсчетов сигнала Х*(со) = 1х*(со) 2х*(со) [ их*(со) J а оценка R определяется соотношением R **ХХ*, где верхний индекс * обозначает переход к сопряженной транспонированной матрице. Строкам матрицы Х*(со) могут быть назначены разные веса. Решение дает следующий алгоритм. 1. Разложение X* = QU, где Q - унитарная (п Хп) -матрица; U - верхняя треугольная (пХш) -матрица вида иЧо (22.1) 2. Для каждого угла приема #: а)прямой ход U*aO>)=c(#), б)обратный ход Uw(tf) =а(#) (а*а)-1, - 1 ~ ~ ~---*¥ Т-1 (22.2 а) (22.26) где а = (U*) -1 с, т. е. а*а = сПГ1 (U*)"*1 с = c*Rс. Весь последующий материал данной главы посвящен разработке процессора адаптивного взвешивания, выполняющего два рассмотренных шага алгоритма. В нем будут использованы две систолические матрицы. Первая - вариант QU-разложения Джентелмена и Кунга [2] - выполняет шаг 1. Вторая - выполняет шаг 2 и является новым решением. 22.2. ПРОЦЕССОР QU-РАЗЛОЖЕНИЯ В этом разделе развиваются результаты, полученные Джентелменом и Кунгом, в нескольких направлениях: комплексные матрицы, вывод данных из матрицы, управление и синхронизация, изготовление ячеек, моделирование больших матриц физически меньшим с помощью декомпозиции задачи. QU-разложение заключается в отыскании такой ортогональной матрицы Q* при которой матрица Q*A = U6btna бы верхней треугольной. Матрица Q* может быть произведением простых ортогональных матриц (вращение Гивенса), каждая из которых выбрана так, чтобы один из элементов А под диагональю был нулем. Для обращения в нуль afj i- и (/-1)-я строки матрицы А заменяются на СИСТОЛИЧЕСКИЕ ЛИНЕЙНЫЕ АЛГЕБРАИЧЕСКИЕ МАШИНЫ 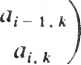 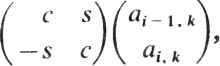 1, 2, m, где (с, 5) выбраны так, чтобы at]- обращались в нуль и матрица была ортогональной : с - ih ai-j.j + <*t.j а Эти элементы могут обращаться в нуль по столбцам снизу вверх в такой последовательности (п, 1), (гг - 1,1), . . . ,(2,1); (и, 2), . . . , 3,2; .. . ; (л, га),..., (га + 1,га). Отметим, что преобразования, обращающие в нуль необходимо применять только к столбцам /, / +1, . .., га, так как во время их выполнения элементыи £ при £</ уже равны нулю. Систолическая структура Джентелмена-Кунга - треугольная процессорная (гаХга)-матрица из гаХга ячеек двух типов, вычисляющая QU-разложе-ние (22.1) входной матрицы размера пХт - показана на рис. 22.1. Кружками обозначены граничные ячейки. На рис. 22.2 показаны функции этих ячеек. Поясним теперь работу таких структур. Во-первых, отметим, что каждая ячейка имеет только одну ячейку памяти. Ее начальное значение равно нулю. Диагональные граничные ячейки вычисляют параметры вращений (с, s). Ячейки (/,/) вычисляют вращения, обращающие в нуль элементы столбца матрицы А. Результаты этих вращений затем перемещаются вправо по строкам процессорной матрицы. Квадратные "внутренние" ячейки осуществляют эти вращения в других столбцах. Матрица А подается на вход структуры сверху в последовательности, показанной на рис. 22.1. Для каждой из ячеек существует момент, когда сверху а 07,2 1,3 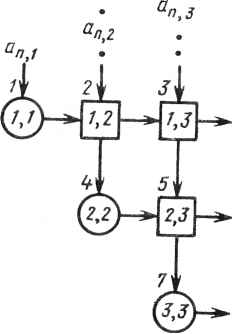 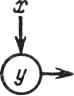 С=Х/)/х2+у2 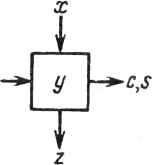 ycx+sy z-~sx+cy Рис. 22.1. Структура Джентелмена-Кунга для QU-разложения Рис. 22.2. Процессорные ячейки QU-структуры слева поступает первый элемент массива А. Предположим, что ап 1 поступает на ячейку (1,1) в момент г = 1. Первый элемент матрицы U, т.е. щ}1,вычисляется в ячейке (1,1) в момент t -п. К моменту времени £ = w + 2(ra - 1) вычисляется последний элемент ит т. Матрица U теперь находится в ячейках памяти структуры. Вращения/определяющие Q*, появятся на правой границе структуры. 22.2.1. Трапецеидальная систолическая подструктура Желательно решать задачи формирования луча различных размерностей, используя одну физическую структуру, поэтому следует решить, как моделировать полную (гаХга)-структуру, используя только ее фрагмент. Предположим, чго мы имеем трапецеидальную структуру размера pXq (рис. 22.3). Пусть В - матрица, содержащая п строк и q столбцов, загружается в верхнюю часть процесса. Вычисляется разложение Q*B = О U2 в2 (22.3) где 0 - нулевая матрица размера (п-р)Хр; Uu - верхняя треугольная матрица размера рХр; U12, В2 - заполненные матрицы с (q -р) столбцами. Матрица В2 выводится из нижней части структуры, a Uu, U12 запоминаются внутри нее. Можно ли получить полное QU-разложение с помощью такой трапецеидальной структуры? Если q не меньше га (числа столбцов А), то сделать это можно; следовало бы обнулить группы из р столбцов матрицы слева направо, используя Гт/pl проходов по матрице. Детали процесса очевидны. Однако если m>q, то решение невозможно. Для проверки предположим, что обнулены первые р столбцов под диагональю при проходе по столбцам 1,2,... Л матрицы. Затем желательно обнулить столбцы р +1,..., 2р при проходе столбцов р + 1, . . . ,p+q. Однако пока не получено вращение после первого прохода для столбцов q +1 , . . ,р +q их нельзя применить для второго прохода. Для обеспечения разложения матриц с числом столбцов, большим q, необходима возможность применения ранее вычисленных и хранящихся в памяти результатов вращения к входным столбцам. Можно придать матрице такое свойство, отключая ячейки крайней левой треугольной части размером pXq и поддерживая активным прямоугольник размером pX(q-p). Параметры вращения вводятся через левую границу. Подмножество из q-p столбцов может поступать в активный прямоугольник сверху. В результате входные векторы, подвергнутые входным вращениям, появляются в нижней части (за исключением первых р строк, которые запоминаются в ячей- Рис- 22-3- Трапецеидальная ках активного прямоугольника).подструктура  22.2.2. Моделирование полной структуры В этом подразделе показано, как можно управлять процессором трапецеидальной структуры, снабженным соответствующей системой памяти для хранения промежуточных результатов, для осуществления разложения при т > >q. Предположим, что множество задач, которые требуется решить, описываются треугольной матрицей пар (/,/): К/</ <га, где пара (/,/) представляет задачу, заключающуюся в применении к столбцу / вращений, с помощью которых обнуляются элементы столбца /. Эта матрица может служить для выполнения шагов "генерации", в которых столбцы действительно обнулены, и "исполнительных" шагов, в которых используются сохраненные в памяти результаты вращения. При генерации осуществляется обработка трапецеидального участка (рхq)-множества исходных пар задачи; при исполнительном проходе осуществляется обработка прямоугольного участка размером px(q-p). Чередование шагов для выполнения всей задачи аналогично покрытию треугольника трапецеидальными и прямоугольными "листами" в соответствии со следующими правилами : 1)трапецеидальные листы должны прилегать к гипотенузе треугольника; 2)ни один лист не может быть размещен, пока не покрыта диагональная сторона слева от него; 3)ни один лист не может быть размещен, если не покрыто пространство непосредственно под ним. Существует множество допустимых вариантов покрытия; на рис. 22.4 показан один из них. При многопроходном получении QU-разложения вырабатываются промежуточные результаты. Они должны запоминаться и позже вновь вводиться в процессор. На рис. 22.5 показана организация памяти. Важными явля- 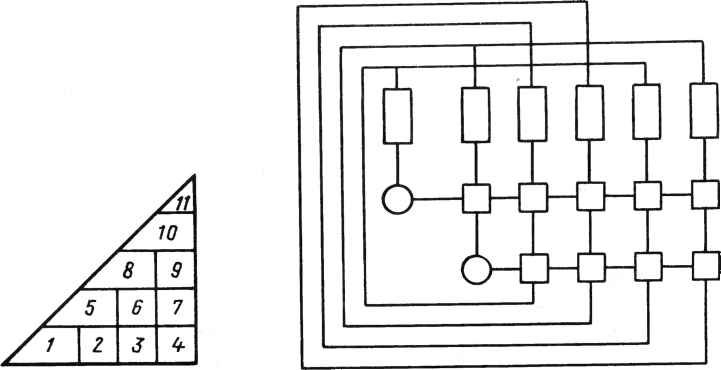 данки памяти Систолическая матрица Рис. 22.4. План проходов при покры- Рис. 22.5. Организация QU-памяти тии "листами" для QU-разложения ООО 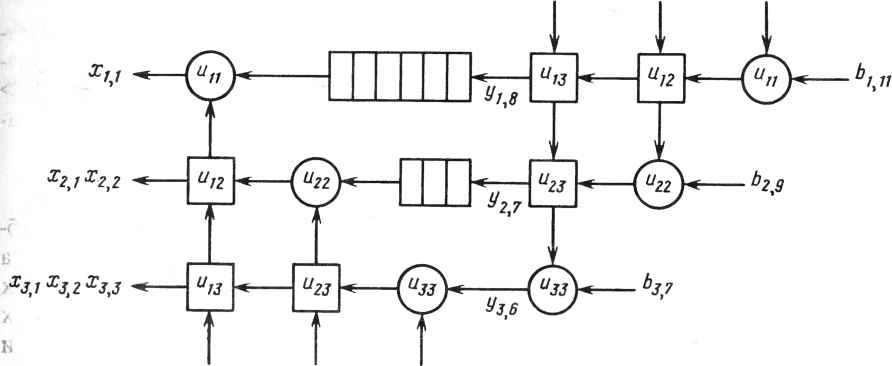 ООО Рис. 22.6. Двухматричная структура прямого и обратного хода ются ее следующие свойства. Имеется отдельный, независимый банк памяти для каждого столбца матрицы. Столбец матрицы запоминается в банке над ячейкой, в которую он вводится впервые. Столбец промежуточных результатов, который появляется из нижней части, пересылается в банк над ячейкой, в которую будет осуществляться следующий ввод. При чередовании шагов в соответствии с рис. 22.4 эти позиции для некоторых столбцов оказываются определенными однозначно, а для других существуют по две возможности. Поэтому соединения в структуре очень просты. Управление структурой также несложно ввиду регулярности путей доступа к данным (рис. 22.6). Адреса памяти могут вычисляться один раз и передаваться из одного банка в следующий. 22.2.3. Другая схема Существует другая возможность, заключающаяся в работе с листами следующих конфигураций: i д-р iii 2(p-f)
р-1 Процессор обрабатывает лист II, активно используя все внутренние ячейки; лист I обрабатывается так же, но с обратным порядком следования 0 ... 60 61 62 63 64 65 66 ... 78 |
|||||||||||||||||||












