Раздел: Документация

0 ... 59 60 61 62 63 64 65 ... 78

где Fn =1 - КкЩ; F12 = Kk. Чтобы проиллюстрировать порядок вычислений, положим, что -i/-й элемент матрицы [Fn ; Fn ]• Коэффициенты матрицы фильтра для заданного диапазона ft]- хранятся в памяти. Эти коэффициенты передаются в процессоры, вычисляющие скалярные произведения для вычисления оценок состояния (см. рис. 21.2). Для расчета оценок состояния используется следующая рекурсивная процедура:

FOR / = 1 torn

= О 1

i¥+1>=*p+fusj / = 1,2,...,л +т Я- = j??+w+1

NEXT /

Так как матрица фильтра имеет размер п X (п + т ), то для расчета этой рекурсии необходимо иметьп+т линейно связанных процессоров.

Поток данных конвейеризованного алгоритма может быть представлен в следующем виде: элементы xiy первоначально равные нулю, продвигаются влево, в то время как элементы sf. продвигаются вправо, a движутся вниз. Все перемещения данных синхронизированы. До того; как данные покинут сеть, каждый процессор скалярного произведения накапливает все произведения, а именно i-2si-2>fi i-\si~\ и • Решающий процес-

сор передает либо данные измерении, либо оценки состояния в процессоры внутренних каскадов в соответствии с приведенной выше рекурсивной процедурой. Эта процедура повторяется до тех пор, пока не будут обработаны все строки матрицы [Fu ; Fl2 J.

Отметим, что в систолическом калмановском фильтре для устранения раздельных процедур загрузки и считывания данные проходят сквозь все процессоры. Каждый из процессоров принимает данные, производит предписанные ему внутренние вычисления и регулярно передает данные дальше. Дополнительно отметим, что соединения процессоров скалярных произведений просты и данные передаются только между соседними процессорами. Это обстоятельство в значительной мере упрощает реализацию систолического калмановского фильтра.

21.4. НЕКОТОРЫЕ ВОПРОСЫ ПРОЕКТИРОВАНИЯ ПРОЦЕССОРА

Рабочие характеристики систолического калмановского фильтра были получены методом имитационного моделирования. Этот этап проектирования особенно важен, так как в систолическом калмановском фильтре одновременно выполняется сразу несколько операций. Моделирование проводилось на ЭВМ VAX 11/750 с целью исследования следующих вопросов реализации: 1) влияния конечной длины слова процессоров скалярных произведений, 2) устойчивости решений уравнений калмановского фильтра, 3) выбора частоты квантования, 4) влияния погрешности округления, и 5) чувствительности оценщика. 376

21.4.1. Анализ устойчивости

Рассмотрим уравнение

=рп4 + рг2У*>(21.32)

где Fu = Ф -КН; F12 =К. Взяв z-преобразование от (21.32), можно показать, что устойчивость определяется корнями многочлена

A(z) =det(zI-Fn).(21.33)

Для того чтобы решение калмановского фильтра было устойчивым, корни A(z) должны лежать внутри единичного круга [15]. Поскольку корни A(z) равны собственным значениям Х( матрицы Fn, решения параллельного калмановского фильтра будут устойчивы тогда и только тогда, когда

IX/K1.

Ввиду неточности моделирования важно проверить грашщы устойчивости, связанные с расчетами калмановского фильтра. На рис. 21.3 дано геометрическое представление запаса устойчивости в z-плоскости. Величина z представляет модуль корней A(z), а A(z)-расстояние от конца вектора z до окружности единичного радиуса. Для выполнения условий устойчивости необходимо, чтобы z +1 Az I < 1. Следовательно, Az может рассматриваться как запас устойчивости. Величина Az зависит от множества факторов, таких как погрешность моделирования и влияние длины слова. Для удобства анализа следует объединить эти факторы в возмущение Fn и анализировать устойчивость собственных значений матрицы Fu + AFn .

Если значение Fn отклоняется до Fu +AFU, то соответствующие изменения собственных значений матрицы Fn могут быть рассчитаны по формуле [16]

АХ,- =vfAFuu/,f = 1,2, ... ,п,(21.34)

где векторы uz- ,vz- удовлетворяют условиям

FnU/ - \(и( =0, uz- =1,

Fnvi -\V/ = 0, vfi*=l.

Если Xj + АХ/ - корни A (z) при отклонении Fn до Fn + AFU, то для устойчивости калмановского фильтра значения X/ + АХ/1 < X/1 + н- ДХ/1 должны лежать внутри окружности единичного радиуса. Таким образом, Az = max 1 </< <иАХ/1 представляет запас устойчивости калмановского фильтра.

(2135) (21.36)

Im zk

Рис. 21.3. Устойчивость в-z-плоскости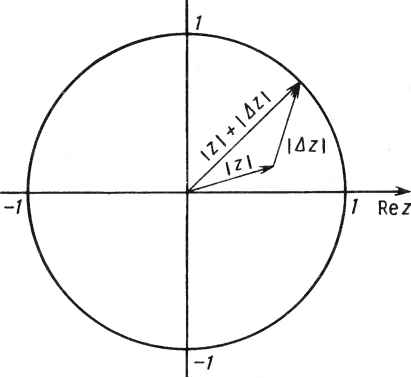

Запас устойчивости =\&z\

---

21.4.2. Выбор длины слова

Выполненный в предыдущем подразделе анализ устойчивости может быть использован для определения минимального числа разрядов, необходимого для обеспечения устойчивости вычислений калмановского фильтра. Чтобы показать это, положим возмущения каждой из составляющих Fn G RnXn рв-ными 2~ь, где Ъ - число разрядов. Тогда AFn оо< (п/2)2~ь, так как элементы Fn< 1 ввиду дискретизации. Далее согласно (21.34) собственные значения возмущенной системы находятся из выражения

X/ + АХг- = \ + yf AFn U/.(21.37)

Условие устойчивости выразится как

IX, +vfAF11u-<X/ + уТА¥пщ\<1.(21.38)

Взяв логарифм от обеих частей (21.38) и выполнив подстановки, получим требуемое соотношение:

Ъ = [ - (1 + log2 ((1 - Amax)/n))] > 0,(21.39)

где Xmax = max 1 </ <иХг- и [(•)] - функция, обозначающая ближайшее целое, превышающее (•)

Формула выбора длины слова (21.39) представляет эффективный метод быстрого определения минимального числа разрядов, необходимого для реализации калмановского фильтра в виде линейно связанной систолической матричной структуры. Модуль максимального собственного значения матрицы Fn является критическим параметром, который влияет на границу устойчивости, и определяется выражением 11 - Xmax = АХ = Az .

Согласно (21.39) был выполнен расчет для различных значений Хтах ил. Результаты представлены на рис. 21.4. Отметим, что число разрядов, необходимое для обеспечения устойчивости, с увеличением п быстро возрастает по мере того, как Xmax -> 1. Вследствие того, что функция Хтах прямо связана с частотой квантования (1/Af), из рис. 21.4 видно, что при больших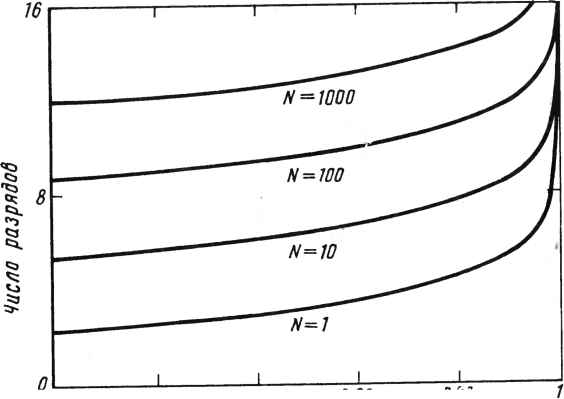

0,90,920,9k 0,960,98

Максимум собственного значения Fn, A mQI

Рис. 21.4. К определению минимального числа разрядов для обеспечения устойчивости калмановского фильтра: N - порядок системы

частотах квантования для сохранения устойчивости вычислении параллельного калмановского фильтра требуется большее число разрядов. Данный анализ показывает, что в систолических калмановских фильтрах при низких частотах квантования могут быть использованы 16-разрядные процессоры, так как при числе разрядов, большем 16, устойчивость увеличивается незначительно.

21.4.3. Выбор частоты квантования

Частота квантования может быть выбрана исходя из рассмотрения чувствительности калмановского фильтра как функции от периода квантования. Например, возвращаясь к калмановскому фильтру (21.32), нетрудно видеть, что Ф и К явно зависят от периода квантования At. Разлагая Ф = ехр(FАг) и К в ряд Тейлора, можно получить следующие аппроксимации этих функций:

ФМ + FAf + ~F2At2 + 0(At3),(21.40)

К = KAt + FKAr2 +0(At3),(21.41)

где F определяется из непрерывной модели (21.5); К - коэффициент усиления калмановского фильтра, полученный из этой, непрерывной модели. Подстановка приведенных аппроксимаций функций Ф и К в (21.32) дает

= [Ф-КН]Х£ + КУ£= [I+(F -KH)Af +1(F2 -2Fm)t2]xk +

+ (KAf + FKAr2)y + 0(At3).

(21.42)

Чувствительность оценки сигнала xk к изменениям периода квантования At определяется выражением

дх

к+1

dAt

(21.43)

где

М = (F - КН) + (F2 - 2FKH)At.

На рис. 21.5 представлена зависимость чувствительности преобразователя от периода квантования типичного случая реализации калмановского фильтра с частотами квантования, намного превышающими частоту Найквиста. Из этой зависимости видно, что на высоких частотах квантования параметр xk более чувствителен к изменениям периода квантования, чем на низких

(21.44)

Рис. 21.5. Зависимость чувствительности оценщика от частоты квантования

200 Ш 600 800 Показатель рекурсии к

1000

---

частотах. Это объясняется более близким расположением собственных значений калмановского фильтра к окружности единичного радиуса; в результате фильтр оказывается более чувствительным к погрешностям округления и дестабилизирующим факторам.

21.4.4. Анализ поведения погрешности округления

Наряду с анализом чувствительности и устойчивости был проведен анализ распространения в калмановском фильтре погрешности округления. Накопление погрешности округления исследовалось на основе основных уравнений процесса:

+А%1 = (fh +AFn) (х* + Дх) + (F12 + AF12) (y + Ay), (21.45)

где AFn и AF12 появляются в результате представления Fn и Fn в памяти

данных с ограниченной длиной слова; Ау - погрешности квантования при

дискретизации. Оставляя только члены (21.45), дающие основной вклад в погрешность, получаем

*k+l + A*k+i =Fux +Fny + гк,(21.46)

где

Bk = Fu Дх* + AFnxk + AF12y + AF12y.(21.47)

Теперь предположим, что погрешность округления £к равномерно распределена в интервале ±£тах, \ек\<тах. Тогда может быть показано, что погрешность округления = хк-хк выражается согласно [12]:

4+1 = рпео = 0.(21.48)

Ковариация погрешности может быть получена из следующих уравнений [12]:

*М=*п*к*п**к>(21.49)

где Rk = Eekek. Соответственно масштабируя Fn для устойчивости калмановского фильтра, можно минимизировать влияние погрешности округления.

21.5. ЗАКЛЮЧЕНИЕ

На основе выполнения операций калмановского фильтра непосредственно на линейно связанной систолической матрице разработана архитектура систолического процессора, реализующего калмановский фильтр. Проведен анализ рекурсивных уравнений для аналитического расчета длины слова, частоты квантования и необходимого объема памяти процессорной ячейки. Анализ показал, что 16-разрядная процессорная ячейка удовлетворяет требованиям обеспечения устойчивости рекурсивных уравнений для низкочастотных вариантов применения при условии, что коэффициент усиления калмановского фильтра рассчитан заранее. Несмотря на то, что результаты, приведенные в данной главе, были получены для калмановской фильтрации, они в основном применимы ко всем известным линейным процедурам.

380

СПИСОК ЛИТЕРАТУРЫ

[I]О. L. Frost and Т. М. Sullivan, "High-Resolution TwO-Pnsional Spectral Analysis," Proc. 1979 IEEE Int. Conf. Acoust. Speech Signal Process АРГ- lwy> PP* 0 /3 0

[2] O. L. Frost, "High-Resolution 2-D Spectral Analysis a* Low SNR," Proc. 1980 IEEE Int. Conf. Acoust. Speech Signal Process., Apr. 1980, pp 580-583.

[3] V. F. Pisarenko, "The Retrieval of Harmonics from Covanance Functions, Feof. J. K. Astron. Soc., 1973, pp. 347-366.

. . rr unique for Unbiased Frequency [4] P. A. Thompson, "An Adaptive Spectral Analyse ТеЧ£

Estimation in the Presence of White Noise, Proc. 15"J

Сотр., New Mexico, 1979, pp. 529-533.

r *i i 44 т . о rs Type Algorithm for Adaptive [5] V. U. Reddy, B. Egardt, and T. Kailath, «ДД. fEEE Trans. Acoust. Implementation of Pisarenkos Harmonic Retrieval *g Speech Signal Process., June 1982, pp. 399-405.

[6] O. L. Frost, "Resolution Improvement in AR Spectral Analysis by Noise Power Cancellation," EASCON, 1977.

[7] V. U. Reddy, R. H. Travassos, and T. Kailath, "A Og*011 °f *°П1шеаГ ***** Estimation Techniques," ISI Tech. Memo 5016-05, Jan- mz

[8] B. D. O. Anderson and J. B. Moore, Optimal Filtering, f rentice-Hall, Englewood Cliffs, N.J., 1979, pp. 267-274.

[9] R. S. Bucy and K. D. Senne, "Nonlinear Filtering Algorithms for Vector Processing Machines," Compl. Math. Appl., 6(3) :317-338 (Mar.

[10] A. Andrews, "Parallel Processing of the Kalman F*lter" InL Соп* Parallel Process., Aug. 1981, pp. 216-220.

[II]R. H. Travassos, "Parallel Kalman Filtering," ISI-04 T**- ReP-> °ct1981-

[12] R. H. Travassos and A. Andrews, "VLSI Implementation of Parallel Kalman Filters » AIAA Guid. Cont. Conf, Advanced Avionics Session, S*n Dleg°» Au8- I982-

[13] E. C. Dudzinski, "Software Optimization of a Kal ™er for ап AP"120B Агг*У Processor," Natl. Aerosp. Electron. Conf, May 1982, pf-221 227*

[14] H. T. Kung, "Communication and Concurrency in Conventional Computers," in Q. Mead and L. Conway, Introduction to VLSI Design, Addison-Wesley, fading, Mass., 1980, pp. 264-270.

[15] В. C. Kuo, Discrete-Data Control Systems, Prentice-Hatf, Englewood Cliffs, N.J., 1980.

[16] Фаддеев Д. К., Фадеева В. Н. Вычислительные МДЫ линейной алгебры. - М.: Физматгиз, 1963. - 734 с.

0 ... 59 60 61 62 63 64 65 ... 78