Раздел: Документация
0 ... 61 62 63 64 65 66 67 ... 78 столбцов, а лист III - с исключением некоторых внутренних ячеек. Лист III может быть обработан только тогда, когда помещается в структуре, т.е. при 2(р - l)<q-p. Сравним последний вариант покрытия с вариантом на рис. 22.4. При первом варианте (рис. 22.4) средний размер листа p(q-p), а при втором - 2p(q - 1)/3. Эти листы используются для покрытия прямоугольников 2(а-1)
Первая схема более эффективна, если p(q-р) >2p(q -1)/3, т.е. при q>3p - 2. Поскольку для второго варианта требуется, чтобы значение q было по крайней мере равно Зр - 2, он никогда не может быть эффективнее первого. 22.2.4.Выбор конфигурации матричного процессора Предположим, что какие-либо причины - например, стоимость - ограничивают размер матрицы величиной pq-pip- 1)/2. Какова наилучшая из возможных конфигурация? На решение влияют два конкурирующих фактора. Полоса частот для обмена меньше для матрицы, близкой к квадратной, так как с окружающими системами связаны только граничные ячейки. Однако число проходов, необходимое для решения задачи, не будет, как правило, минимально при p-q. Для типичного случая [скажем, при т = 100, pq ~-р{р - 1)/2 = 31] при оптимальной конфигурации матрица может быть достаточно узкой (в данном примереp = 2,q = \6). 22.2.5.Вывод данных из памяти ячеек Трапецеидальный матричный QU-процессор выполняет разложение матрицы (22.3). Однако, как выводить элементы Un и U12, хранящиеся в ячейках матрицы? Построим схему со следующими свойствами: 1)выходной поток данных полностью однороден; 2)управляющие сигналы поступают только на граничные ячейки; 3)для внутренних ячеек не требуется никаких функций с особым управлением; 4)процессор может заканчивать разложение матрицы, выводить содержимое памяти ячеек и начинать разложение следующей матрицы без какой-либо задержки. Ключевым моментом схемы вывода данных из памяти является поведение ячейки при передаче ей "единичной" функции вращения (с = 1, 5=0). В этом случае ячейка работает как элемент единичной задержки: У Для начала предположим, что за входной матрицей А следует матрица В. Данные будут подаваться в процессор в следующем формате: Ь пт 0 Ъп2 . dim Ьп1 0,(22.4) 0 а12 \ I так, что две обрабатываемые матрицы разделены диагональю нулей. В результате процессор будет "выталкивать" U сразу по получении результата и заполнять каждую ячейку нулями непосредственно перед тем, как элемент поступит в нее. Следовательно, процессор "рассматривает" новую матрицу В таким образом, как если бы она первоначально содержала только нули. Когда элемент В впервые поступает на граничную ячейку, в ней содержится нуль (это будет показано позже). Обычной функцией граничной ячейки (см. рис. 22.2) является запоминание абсолютной величины этого элемента в ее памяти и выдача "единичной" функции вращения, если элемент был неотрицательным, или произведения -1 на "единичную" функцию вращения в противном случае. По мере продвижения результата вращения вправо встречаются ячейки, содержащие в памяти нули, эти нули выталкиваются и замещаются элементами (возможно, отрицательными) строки матрицы В. Таким образом, нули передвигают столбцы вниз по всей матрице процессора. Теперь покажем, как учитываются элементы U. Положим, что время г = 0 есть время ввода в ячейку (1,1) элементами . Тогда ячейка (/,/) принимает последний элемент матрицы А и вычисляет элемент матрицы В в момент t =/+/ - 2, тем самым работа заканчивается. В соответствии с принятой здесь последовательностью ввода (см. рис. 22.4) нулевые данные появляются на входе ячейки (1»/) в момент / непосредственно после вычисления щ j. Для обеспечения правильной работы процессора желательно получить в то же время единичное вращение, обусловливающее выталкивание элемента и xj и загрузку нуля. Это может быть реализовано специальной функцией граничной ячейки. Положим, что в цикле 1 ячейка (1,1) выполняет операцию С=1 s=0 с7 Операция вращения, сформированная таким образом, достигнет ячейки (1, /) в момент /, как и требуется. Далее, положим, что в момент времени 3 ячейка (2,2) выполняет ту же операцию: и zz (Элемент и12 был вытолкнут из первой строки, как описывалось ранее.) Эта операция вращения будет передана далее для выталкивания элементов и2Л из ячейки (2, к) и загрузки и lM = 3, 4, . . . , q. В момент времени 4 эта специальная функция вновь потребуется в ячейке (2,2): s=0 гг Данное вращение следует за предыдущим вниз по строкам, выталкивая элементы ulk и загружая нули. В общем случае ячейка (к,к) выполняет данную специальную функцию к раз в моменты времени t = 2к - 1,..., Зк - 2. Затем единичное вращение движется ниже строки к, выталкивая строки к, к - 1,. . ., 1 матрицы и загружая нули, предшествующие следующей матрице. Для обеспечения однородного вывода из процессора следует добавить несколько ячеек внизу слева для получения прямоугольной структуры: 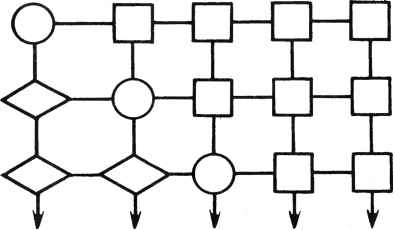 Единственным назначением ромбических ячеек является задержка окончательного вывода элементов U, которые выходят теперь из процессора в том же формате, что и элементы А (элементы i,j выходят в момент времени га- i +/). 22.3. МАТРИЧНЫЙ ПРОЦЕССОР ДЛЯ ОБРАТНОГО ХОДА Для решения треугольной системы UY = В (матрицы Y и В имеют размеры тХп) можно использовать треугольную структуру, показанную на рис. 22.1. Детали устройства такой структуры достаточно очевидны и не приводятся. Отметим лишь, что оно состоит из треугольного массива процессорных ячеек, каждая из которых подобно матрице Джентлмена-Кунга содержит один элемент матрицы U, так что для решения некоторых прикладных задач может быть полезна одинаковая реализация обеих структур. В рассматриваемых примерах значение п часто может быть довольно велико. Пусть требуется решить две системы: UY = В и UX= Y, но элементы Y не представляют интереса. Если X хранится в памяти, то там же можно хранить и Y. Предположим, однако, что X не хранится в памяти. Можно задаться целью минимизировать объем промежуточной памяти для хранения Y. Он может быть сокращен до О (га2) ячеек двумя способами. Можно использовать еще одну структуру для решения UX = Y и направлять результаты первой структуры во вторую. При этом необходим интерфейс из Зга (га - 1)/2 ячеек задержки, как показано на рис. 22.6. Другой возможностью является использование одной и той же структуры для решения обеих систем одновременно. На рис. 22.8 показаны два последовательных цикла работы такого устройства. В каждый данный момент половина диагоналей работает над одной системой уравнений, а другая половина диагоналей - над другой. В этом случае необходима матрица из (Зга2 - 2га) /4 ячеек задержки, что приблизительно вдвое меньше, чем в двухматрич-ной структуре. Рис. 22.7. Структура для решения уравнения Lr Y - В 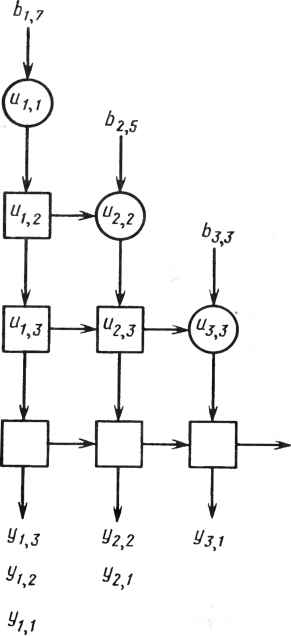 (ylt+yis+fflt) 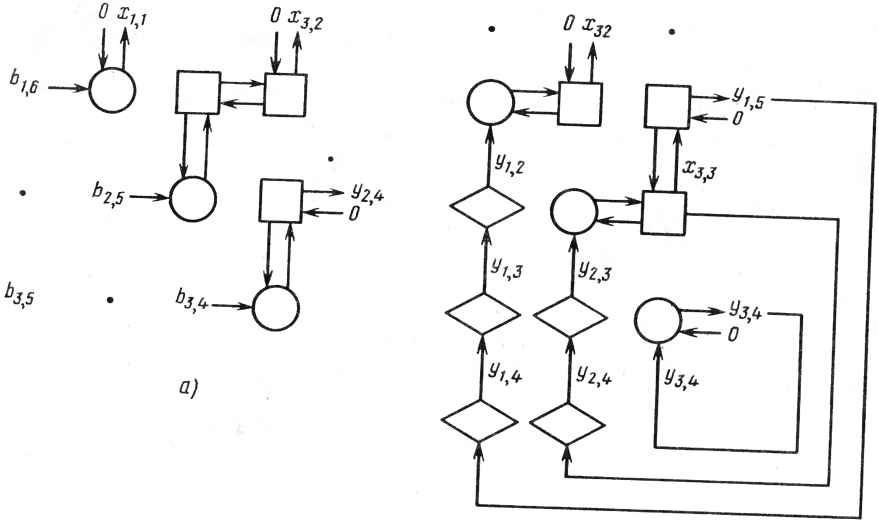 S) f-CUH2inHrPHaaдаЯ ПРямого и обратного хода- а - цикл 11; б - цикл 12 22.3.1. Вычисление масштабных коэффициентов Вычисление (22.26) требует масштабного множителя а*(#)а(#), т.е. скалярного произведения решения системы (22.2а) на себя. Поскольку векторы решения а получаются поэлементно (один элемент за цикл) с последовательных столбцов матричного процессора, эти скалярные произведения можно накапливать, присоединив строки ячеек к нижней части матрицы (см., например, рис. 22.7). 22.4. КОМПЛЕКСНОЕ QU-РАЗЛОЖЕНИЕ В действительности должны обрабатываться комплексные матрицы А. Конечно, можно решить комплексную (2пх2т)-задачу наименьших квадратов с помощью QU-разложения действительной матрицы размера 2пх2т ar -aj 1 А/A* J где А = Ад +jA7 - результат разложения матрицы А на вещественную и мнимую части. Однако при использовании вращений Гивенса это требует в 8/3 раз больше операций вещественного умножения, чем при непосредственном комплексном QU-разложении матрицы А. 392 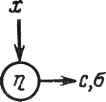 Су6 с = х/д 6=п/Р П = ? т с.б у =с*х+бу z=-6x+cy Операция QU-разложения является единственной только с точностью до умножения строк матрицы U на коэффициенты с модулем 1: A = (QD)(D *и) - также QU-разложение при любой унитарной диагональной матрице D. Поэтому необходимо, чтобы диагональные элементы U были положительными вещественными. Это и есть единственная функция разложения, вычисляемая рассматриваемой структурой. Изменим описания ячеек на рис. 22.1 на описания, представленные на рис. 22.9. Договоримся обозначать строчными латинскими буквами комплексные величины, а греческими - вещественные, т.е. а =а + jcv, х =f + j£ , Рис. 22.9. Процессорные ячейки для комплексного QU-разложения где j = \j-l. Такие ячейки, конечно, более сложны в реализации, чем вещественные ячейки Гивенса. Далее мало что меняется. Когда первый элемент входной матрицы оказывается в граничной ячейке, происходит следующее: й © с~ а/\а\ Таким образом, вместо единичного вращения, реализуемого в вещественном варианте, осуществляется унитарное диагональное вращение. 22.5. РЕАЛИЗАЦИЯ СБИС В этом разделе обсуждается, как могут быть выполнены внутренние ячейки вещественной и комплексной QU-матриц, а также комплексной матрицы для обратного хода при использовании внутреннего систолического кристалла (ВСК), разработанного фирмой ESL. Следует особо отметить, что эти ячейки можно получить, используя одни и те же блоки на СБИС без дополнительных микросхем. Более того, мы использовали ВСК для построения и других смешанных ячеек для вещественного или комплексного QU-разложения. Вполне вероятно, что систолические матрицы для большинства стандартных алгоритмов линейной алгебры могут быть получены на данном кристалле .и еще на одном, к которому обратимся позже. Сначала дадим краткое описание ВСК. Он спроектирован на основе КМОП-технологии с разрешением 2 мкм фирмы ESL. Его функции таковы: 0 ... 61 62 63 64 65 66 67 ... 78 |
|||||||||||||||||||||||||||












