Раздел: Документация
0 ... 56 57 58 59 60 61 62 ... 78 нозначной циклической свертки [ук двух TV-точечных целых последовательностей ;cwj и {hm} N- 1 У к = Z Хп Кк - п) и = 0 (20.3) результирующие значения должны находиться внутри диапазона, ограниченного значением Ft, где (к - п) представляет собой остаток от (к - п) по модулю N. Этого можно достичь, если Ук N - 1 ]Г А„ /l(/c -п) п = 0 n - 1 < I I I (к п) I (20.4) п = 0 Пусть шах хп = max \hrn\ -А - максимальное значение переменных xw и hm - называется динамическим диапазоном xw и Чтобы ограничить значение \ук в соответствии с (20.4), достаточно положить \/Tl/(2A0j,(20.5) где [х] означает наибольшее целое, меньшее, чем х. Однако для многих практических задач это значение А слишком пессимистично. В данной главе Ft, а и А выбираются равными F5 =232 + 1, у/2 и 128 соответственно. Поэтому данные ЧПФ являются целыми числами от 0 до 232. Следовательно, для представления числа достаточно 33 разрядов, а длина преобразования равна 128. В ЧПФ над Ft величина у/Т представляет целое 22?~2 (22 -1) [4,5]. Для г =5, так как 232 = -1 (niodF5), \/2"=224-28 =224+240. Заниженное значение динамического диапазона составляет у/232/(2 • 128) = 212 [12]. Это значение является достаточно * большим для подавляющего числа практических задач. Для облегчения выполнения двоичных арифметических операций, необходимых для реализации схем ЧПФ, предложено два представления двоичных чисел [13, 14]. В дальнейшем используется представление "с уменьшением на 1", предложенное Лейбовицем. Пусть А представлено в виде [а32а31 .. .а1а0], где 0< <Л <232 и ai есть/-й двоичный разряд числа А. В табл. 20.1 показано соответствие между десятичными числами в нормальном двоичном виде и их значениями в представлении "с уменьшением на 1". В последнем случае самый старший разряд а32 равен 1 тогда и только тогда, когда значение целого числа равно 0. Таким образом разряд а32 может быть использован как признак равенства нулю. Для определения ЧПФ необходимы две основные двоичные арифметические операции - сложение и умножение на степень числа 2 по модулю Ff. Другие операции могут быть выражены через эти две. Далее кратко описываются операции сложения и умножения. Более детальное изложение можно найти в работе [14]. \ 1. Сложение. Пусть S=A +В. а) Если А =0, то S=B. б) Если 5 = 0, то 5 = =А. в) Если ни А, ни В не равны 0, то сложить [я31Язо • • -яо] и [Ь31зо • • • .bxb0]. Затем получить дополнение к цифре переноса и прибавить его к предыдущей сумме. Это и даст S. Таблица 20.1 ----Представление Двоичное представление"с уменьшением на 1"
2.Умножение на степень числа 2. Пусть В-А 2е. а) Если А=0, то В = 0. б) Если А ф 0, то выполнить циклический сдвиг [аао .. .аха0] на С разрядов влево, значение 31-го разряда заменить на его дополнение, если он в результате сдвига попадет на место 0. Наконец положить Ъ32 =0. 3.Вычитание. Так как 232 = -1 (mod F5), -А =А -232. Следовательно, если АфО, -А= [а32а3{а30 .. .aia0]9 где at обозначает дополнение а(. Если А = 0, то -А = 0. 4.Умножение на у/2. Так как у/2 = 234 + 240, А у/2 =А - 234 + А • 240. 5.Умножение на степень у/2. Пусть В-A (y/l)c. Если С четно, то 5 = =Л • 2е/2. Если С нечетно, тоВ=(А у/2) •2<с~1>/2. Сложение 0»0 0 07 0 +) 1/ 0 7 / Сложение 1 3 Сложение +) 010 7 #! 7 7 2 4 +) 1\0 О 0 0 0 0 1 Сложение +) 0\0 1 0\1 0 2 3 0\1 1 4 +) J7J / 0 J 01 7 / 7 0 7 7 0 0 0 0 7
б) Рис. 20.1. Примеры двоичных операций по модулю Fx шением на 1: д - сложение; б - умножение на степень числа 2 22 +1 в представлении с умень- 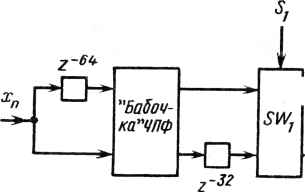 Z-32  -16 1 sw2 -16  •-HZ} г-* Примеры, приведенные на рис. 20.1, иллюстрируют операции сложения и умножения на степень числа 2 по модулю Ft. Для простоты Ft на рис. 20.1 выбрано равным Fx = 22 + 1. В этом случае для представления целого числа достаточно трех двоичных разрядов. На рис. 20.1 использовано представление "с уменьшением на 1". 20.3. КОНВЕЙЕРНАЯ СТРУКТУРА ДЛЯ 128-ТОЧЕЧНОГО ЧПФ Согласно (20.1) математический алгоритм ЧПФ похож на алгоритм БПФ. Следовательно, для выполнения быстрого ЧПФ можно использовать почти точный аналог структуры типа БПФ. На рис. 20.2 показана конвейерная структура типа БПФ [1] для выполнения 128-точечного ЧПФ над полем Fs. Эта структура может рассматриваться как одномерная систолическая матрица. Ее основными элементами являются элементы задержки, коммутаторы и элементы выполнения операции "бабочка" БПФ. В структуре эти основные элементы чередуются, а используемый метод представляет собой метод прореживания по времени по основанию 2. Схема выполнения обратного ЧПФ представляет собой зеркальное отображение схемы, показанной на рис. 20.2, в которой используется техника прореживания по частоте по основанию 2. На рис. 20.2 z~J означает элемент задержки на / тактов. Этот элемент может быть реализован в виде множества из 33 сдвиговых регистров, состоящих из / ступеней. Коммутаторы SWt управляются сигналом где 1 </<6. Операции, осуществляемые коммутаторами SWfy показаны на рис. 20.3. Управляющие сигналы Sj могут быть просто получены с помощью шестиразрядного счетчика прямого счета, если в бабочке ЧПФ не используются буферные регистры [1]. Если же в бабочке ЧПФ буферные регистры используются, то на выходах счетчиков для синхронизации необходимо включать элементы задержки, как показано на рис. 20.4. На рис. 20.5 приведены условное обозначение и математическая запись операции бабочка ЧПФ с прореживанием по времени. Аналогичная бабочка с прореживанием по времени для ЧПФ была разработана в [13]. Структурная схема устройства, реализующего бабочку ЧПФ с прореживанием по времени, приведена на рис. 20.6. На этой схеме А, В, ОиЕ представляют собой 33-разрядные числа, а С - 7-разрядный порядок числа а в (2Q.1), т. е. С=пк mod Ж Два способа реализации сумматора ЧПФ можно найти в [13]. Один из них показан на рис. 20.7. Умножитель на рис. 20.6 используется для умножения числа на степень числа 2 по модулю Fs. Схема этого умножителя приве-360 Рис. 20.2. Конвейерная структура для выполнения 128-точечного ЧПФ
к2к *2к+1 Рис 20.3. Коммутатор: а - прямое соединение; б ное соединение - перекрест- 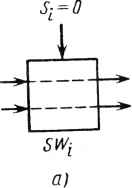 5; =/ 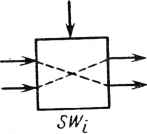 б) 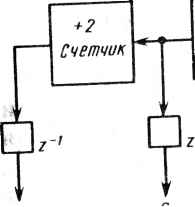 +2 Счетчик -{?mod25) +2 Счетчик +2 Счетчик +2 Счетчик +2 Счетчик Синхросигнал т т -[Ьтт>2J) (5mod2z) -(6/rwd2f) S5S6 S,д2 Рис. 20.4. Шестиразрядный суммирующий счетчик для формирования управляющих сигналов 5Z- на рис. 20.1 в -k-BiVzf Рис. 20.5. Условное изображение (а) и математическая запись {б) операции »бабочка" ЧПФ с прореживанием по времени 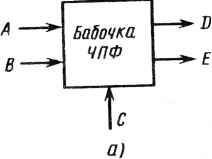 б) 33 Регистр я* 33 Регистр Мультиплексор Мультиплексор V2 -1 Гб~ CqLCj : с6] Инвертор С 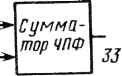 Сумматор ЧПФ 33 п ппапопнн "бабочка" ЧПФ с прореживанием по времени Рис. 20.6. Структурная схема операции оаоочка чи * 1 361 -7 32 32
Х32 32 "7 32 33 43 Рис. 20.7. Структурная схема сумматора ЧПФ, выполняющего операцию Z =Х+ У (mod F.) В (ьзг -I л» МодифицароОанный сдвиговый регистр ши- J2 Мультиплексор 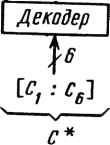 Рис. 20.8. Схема выполнения операции В- 2С
0
S3S2S1S0 bo a) 5) Рис. 20.9. Таблица истинности (а) и схрмя /vn pa для ЧПФ над полем F, =22 +1модифицированного сдвигового регист- дена на рис.20.8. Регистр на рис. 20.8 является модификацией сдвигового регистра [15] для выполнения операции циклического сдвига. В качестве примера рассмотрим простое ЧПФ над полем F\ = 22 + 1. На рис. 20.9 показана таблица истинности и схема модифицированного сдвигового регистра для бабочки ЧПФ; входными величинами в этой схеме являются [ЬгЬо] и [s3s2s!sоL а выходными - [bfb$]. 20.4. АРХИТЕКТУРА ЦИФРОВОГО ФИЛЬТРА С ПРОИЗВОЛЬНОЙ ДЛИНОЙ ПРЕОБРАЗОВАНИЯ ЧПФ В предыдущем разделе были выбраны значения Ft=F5, gl~\J2 и N- 128. Максимальная длина преобразования над полем F5 равна N~ 128 [2,3] и динамический диапазон равен 212. Длину преобразования можно увеличить, выбрав Ft при t > 6. В таком случае, однако, для представления числа требуется по крайней мере 26 + 1 = 65 разрядов. Другим вариантом увеличения длины преобразования является выбор а, при котором а уже не является степенью числа над полем F3 или F4. В таком случае необходима операция полного умножения. К тому же динамический диапазон может быть недостаточным. Для преодоления этих трудностей при вычислении линейной свертки последовательностей (входных данных и импульсной характеристики) произвольной длины обобщается метод перекрытий с накоплением. В итоге разработана параллельная архитектура системы, реализующей обобщенный метод перекрытия с накоплением при использовании 128-точечной схемы ЧПФ, рассмотренной в предыдущем разделе. Пусть {хп} и {hm} - входная последовательность и импульсная характеристика фильтра соответственно, где 0</z <./V- 1 и 0<m<M - 1. Выходная последовательность {у} фильтра представляет собой линейную свертку {хп) n{hm} , где 0<k<N+M-l [13]. В дальнейших рассуждениях предположим, что 7V= 128 иМ =256. Чтобы вычислить \ук \ с использованием 128-точечного ЧПФ, сформируем четыре 128-точечные характеристики [h ут }, j/z ] , \h } и \ }\ *т \ разделив { т] следующим образом: п т hm для 64 (i - 1) <га< 64/ - 1, 0 в противном случае(20.6) Для 1 <i <4. Далее результат {у*%\ линейной свертки и {/7} вычисляется с помощью техники циклической свертки. Значение \у\\ вычисляется стандартным методом перекрытий с накоплением [1] и ЧПФ. С этой целью \хп] разделяется на 128-точечные подпоследовательности {xJn \ , каждая из которых перекрывается в 64 точках {хп } с любыми двумя смежными подпоследовательностями , где/ > 0, т.е. / = J хп для64(/-1)<72<64(/ +1) -1, п ]0 в противном случае.(20.7) 0 ... 56 57 58 59 60 61 62 ... 78 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












