Раздел: Документация
0 ... 55 56 57 58 59 60 61 ... 78 /1 °crt x jt x Входные данные {Ч потока \ комплексных Величин) 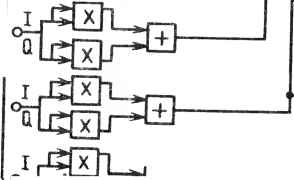 ,J1 -пг + Усредняющие коэффициенты 1 Буфер буфер 1 им Да- буфер I буфер Спектральная плотность мощности -** ( 4 канала) Усредненная СПИ* (4 канала) Рис. 19.7. Структурная схема блока вычисления спектральной плотности мощности сивной процедуры усреднения. Структура этого элемента показана на рис. 19.7. После вычисления модулей комплексных входных данных выполняется операция их усреднения. Процедура усреднения включает поточечное суммирование текущего спектра с частью ранее накопленных значений. Для построения такого блока потребуется примерно 90 ИС. Блок основной операции фильтра. Основные операции фильтра реализуются с помощью универсальной мини- или микроЭВМ. Передаточная характеристика фильтра может быть фиксированной или подстраиваемой в зависимости от применения системы. Универсальная ЭВМ не учитывается при оценке сложности системы, поскольку в большинстве систем имеется главная ЭВМ, которая и будет выполнять указанную функцию. Блок объединения. Выходы блоков обратного БПФ и перекрывающегося обратного БПФ мультиплексируются в блоке объединения, как показано на рис. 19.8. Все входные данные преобразуются к уровням элементов ЭСЛ. Затем эти данные с помощью двухуровневого мультиплексора 8 :1 образуют один выходной канал. Технически это реализуется на базе двух мультиплексоров 4:1, выходные сигналы которых поступают в мультиплексор 2:1. В состав блока объединения входят 143 ИС. 352 Обратное БПФ (и канала) / Обратное перекрывающееся БПФ (4 канала) о- о-
ТТЛ-ЗСЛ ттл-эсл ттл-эсл ттл-эсл Мультиплексор 4:/ Мультиплексор 4-7 Мультиплексор 2-1 Выходные сигналы во временной области Рис. 19.8. Структурная схема блока объединения 19.4. ПОЛНАЯ СТРУКТУРА ФИЛЬТРА Как показано в табл. 19.1, для построения фильтра, выполняющего полную обработку в частотной области (включая два канала совмещенной обработки и два блока вычисления обратного БПФ), потребуется 49 печатных плат, содержащих около 6100 ИС и рассеивающих мощность примерно 6 кВт. Устройство компонуется на печатных платах, содержащих от 78 до 179 ИС при рассеиваемой мощности от 100 до 150 Вт. Размеры 22,5X40 см каждой печатной платы, что позволяет использовать промышленные шасси для их крепления (для макетирования) и монтажные платы промышленного производства. Печатные платы устанавливаются в четырех выдвижных секциях стандартной стойки для оборудования. Каждый из четырех процессоров для выполнения соответствующих БПФ (прямого, пе рек рыв ающе гося прямого, обратного и перекрывающегося обратного) размещается в отдельной выдвижной секции. Суммарный объем фильтра в настольном варианте исполнения, обеспечивающего полную обработку в частотной области, составляет около 305 см3. Входные данные поступают со скоростью 4 • Ю7 оп./с (эквивалентной 128 Гбит/с, если входные данные являются комплексными 16-разрядными словами). Частота данных на выходе фильтра та же самая 4 • 107 оп./с. После выполнения соответствующих операций в блоках предварительной и весовой обработки все последующие вычисления выполняются с помощью 22-разрядного арифметического устройства с плавающей запятой (6 разря- Таблица 19.1. Параметры, характеризующие сложность процессора Назначение блокаЧисло бло- Общее чис- Общая мощ- ков ло кристал- ность, Вт лов
дов которого используется для порядка и 16 - для мантиссы) для обеспечения точности и исключения необходимости применения адаптивного масштабирования. 19.5. ЗАКЛЮЧЕНИЕ В этой главе проиллюстрированы потенциальные возможности достижения производительности около 109 оп./с, эквивалентных бабочке БПФ при основании 2, на базе современной технологии СБИС. В табл. 19.2 приведены обобщенные характеристики фильтра, выполняющего полную обработку в частотной области. Двумя наиболее существенными характеристиками являются: скорость вычислений на единицу объема (960-106 бабочек БПФ в секунду при объеме 305 см3; примерно 108 таких операций в секунду при объеме 30,5 см3) и рассеиваемая при такой скорости мощность (примерно Таблица 19.2. Характеристики фильтра в частотной области (технология 1982 г.)
170 • 103 бабочек БПФ в секунду на 1 Вт рассеиваемой мощности). Эти цифры и скорость вычислений могут рассматриваться как перспективные, если учесть, что система SPS-1000 с четырьмя блоками конвейерной обработки обеспечивает выполнение около 42 • 106 бабочек БПФ в секунду [8]. В этой системе скорость вычислений на 1 дм3 составляет (1,8 - 3,6) • 106 бабочек БПФ в секунду. Другой высокопроизводительный процессор достигает значения скорости вычислений (при 16 вычислительных элементах) около 71 • Ю6 бабочек БПФ в секунду [9]. Таким образом, разработки на базе СБИС обеспечивают увеличение производительности примерно на порядок по сравнению с любой из описанных серийно выпускаемых систем. Это исследование, конечно, не определяет верхнюю границу производительности процессора. Можно ожидать, что в ближайшем будущем при усовершенствовании технологии микросхем типа ЭСЛ или на основе GaAs смогут быть достигнуты скорости вычислений около 10й бабочек БПФ в секунду. СПИСОК ЛИТЕРАТУРЫ [1] J. Н. McClellan and R. J. Purdy, "Applications of Digital Signal Processing to Radar," in A. V. Oppenheim, ed., Applications of Digital Signal Processing, Prentice-Hall, Englewood Cliffs, N.J., 1978, Chap. 5. [2] F. J. Harris, "On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform," Proc. IEEE, 66:51-83 (1978). [3] C. D. Bergland, "Fast Fourier Transform Hardware Implementations-An Overview," IEEE Trans. Audio Electroacoust., A£/-/7:104-108 (1969). [4] J. A. Eldon and C. Robertson, "A Floating Point Format for Signal Processing," Proc. ICASSP-82, 1982, pp. 717-720. [5] J. W. Cooley and J. W. Tukey, "An Algorithm for the Machine Calculation of Complex Fourier Series," Math. Сотр., 79:297-301 (1965). [6] H. L. Groginsky and G. A. Works, "A Pipeline Fast Fourier Transform," IEEE Trans. Comput., C-79:1015-1019 (1970). [7] A. Kanemasa, R. Maruta, K. Nakayama, Y. Sakamura, and S. Tanaka, "An LSI Chip Set for DSP Hardware Implementation," Proc. ICASSP-81,1981, pp. 644-647. [8] R. A. Collesidis, T. A. Dutton, and J. R. Fisher, "An Ultra-High Speed FFT Processor," Proc. ICASSP-80, 1980, pp. 784-787. [9] C. S. Joshi, J. F. McDonald, and R. H. Stinvorth, "A Video Rate Two Dimensional FFT Processor," Proc. ICASSP-80, 1980, pp. 774-778. ПАРАЛЛЕЛЬНАЯ СБИС-АРХИТЕКТУРА ЦИФРОВОГО ФИЛЬТРА ИСПОЛЬЗУЮЩЕГО ТЕОРЕТИКО-ЧИСЛОВЫЕ ПРЕОБРАЗОВАНИЯ Г. Труонг1,И. Рид, К Йе, Г. Чанг, X. Мао2 20.1. ВВЕДЕНИЕ Для решения многих практических задач цифровой обработки сигналов требуется циклическая свертка [1]. Для эффективного выполнения циклических сверток были развиты как быстрое преобразование Фурье (БПФ), так и теоретико-числовое преобразование (ТЧП). Циклическая свертка двух последовательностей целых чисел получается в результате обратного ТЧП, применяемого к результату ТЧП двух последовательностей. В частнос-ти, при цифровой фильтрации [4, 5], обработке изображений [8, 9], восстановлении рентгеновского изображения и при кодировании и декодировании некоторых кодов Рида-Соломона [4, 12] может быть использовано числовое преобразование Ферма (ЧПФ). Теоретико-числовые преобразования обладают следующими преимуществами перед обычным БПФ: 1) для некоторых из них не требуются операции умножения; 2) используется арифметика целых чисел; 3) нет ошибок округления. Недостатками ТЧП являются: 1) противоречие между длиной преобразуемых последовательностей и шириной динамического диапазона при приемлемых размерах слова, что часто ограничивает применимость этого преобразования; 2) арифметика преобразования требует операций над классами вычетов по модулю некоторого простого числа. Важным видом ТЧП является числовое преобразование Ферма. Преимущество ЧПФ перед большинством ТЧП состоит в том, что длина преобразования равна степени числа 2. В результате для выполнения ЧИФ может быть использована структура БПФ; число 2 является возможным корнем из единицы в некотором конечном поле или кольце. Вместе с ЧПФ, которое имеет число 2 в качестве корня единицы, операции умножения на степень числа 2 по модулю числа Ферма легко выполняются посредством циклического сдвига слова в двоичной арифметике. С другой стороны, БПФ требует умножения на комплексные корни единицы, имеющие вид e2njnk/N. В [13] приводится описание аппаратной системы для реализации 64-точечного ЧПФ над 17-разрядными числами на основе серийно выпускаемых ЭСЛ ИС. Для этой аппаратной реализации ЧПФ было разработано нестандартное представление двоичных чисел, которое использовалось для выполнения двоичных арифметических операций по модулю чисел Ферма. Для этой цели Лейбовицем [14] было разработано простое представление двоичных чисел. В данной главе излагается обобщенный метод перекрытия с накоплением для разрешения противоречия между длиной преобразуемых последователь- 1Калифорнийский технологический институт, Пасадина, Калифорния. 2Университет Южной Калифорнии, Лос-Анжелес, Калифорния. ностей и размером динамического диапазона. На основе этого метода с помощью ЧПФ разработана параллельная архитектура реализации цифрового КИХ-фильтра с импульсной характеристикой произвольной длины. В разд. 20.2 кратко рассматривается ЧПФ, представление двоичных чисел, предложенное Лейбовицем, и требуемые двоичные операции по модулю чисел ферма. В разд. 20.3 представлена конвейерная структура выполнения 128-точечного ЧПФ над полем F5, удобная для реализации на СБИС. При такой структуре требуются только операции сложения и циклического сдвига. Циклический сдвиг, необходимый для выполнения операции умножения на степень числа 2, может быть реализован модификацией стандартной схемы циклического сдвигового регистра [15]. В разд. 20.4 детально прорабатывается обобщенный метод перекрытия с накоплением для выполнения линейной свертки двух последовательностей произвольной длины. В конечном итоге разрабатывается параллельная архитектура систолического типа для реализации обобщенного метода перекрытий с накоплением, при этом используются схемы прямого и обратного ЧПФ на 129 отсчетов. Эта регулярная и допускающая расширение архитектура удобна для исполнения в виде СБИС. 20.2. ЧИСЛОВОЕ ПРЕОБРАЗОВАНИЕ ФЕРМА Пусть Fx =22* +1 есть Г-е число Ферма, где t>0. Число Ft является простым для 0<Г <4. Пусть \хп} есть А-точечная последовательность целых чисел, где 0<ап <Ft - 1, 0<n<N- 1 и N - степень числа 2. Числовое преобразование Ферма {Xkj последовательности (xnj над Ff определяется следующим образом : N-l Хк= Ъ хпапк (mod Ff),0<k <N~ 1,(20.1) где 0<Хк<Ft - 1; а - корень iV-й степени из единицы, т.е. А- наименьшее положительное целое число, такое, что ot = 1 (mod Ff). Соответствующее обратное преобразование ЧПФ определяется как 1 N-l *„ = - £ Хка~пк (mod F,), 0<n<N- 1,(20.2) N к=о где 1/N - число, обратное Nno модулю Ft. (Таким образом, 1 /Атакже целое число.) В уравнениях (20.1) и (20.2) показатели степени предполагаются взятыми по модулю N. Циклическая свертка вычисляется с помощью преобразований ЧПФ (20.1) и (20.2). Длина преобразования N зависит от Ft и а, выбираемых, как в [4,5]. Более детальное изложение ЧПФ можно найти в [4,5]. Чтобы найти свертку без переполнения с помощью ЧПФ над полем Ft, необходимо ограничить диапазон изменения переменных. Для вычисления од- 357 0 ... 55 56 57 58 59 60 61 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












