Раздел: Документация
0 ... 43 44 45 46 47 48 49 ... 96 при определении методов обработки. Но следует учитывать, что на производстве одновременно изготавливают множество деталей. Отсюда возникает последовательность организационно-технологических задач: определение минимального количества технологического оборудования - задача целочисленного программирования; определение минимального количества инструментов и т.п. 2.2.2. Основные математические понятия М - множество. т - элемент множества. тМ - принадлежность. тМ - непринадлежность. Множество задается: 1.Перечислением элементов: М ={Wj}, i = \,k. 2.Условиями: А={а / Fj,F2,...}; F\, ••• - условия. A={a=C / ReC=0}, С - множество комплексных чисел, а - чисто мнимые числа. Операции над множествами. Объединение А - М и N; «u»- объединение. A={a/aeMvae N}; «v» - или. v (или) - логическая операция задается таблицей истинности (см. табл.2.) Например, X, У, Z - логические переменные, принимающие значения 1 и 0. Таблица 2
Изображение на кругах Венна 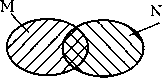 А = М u N; «и» или Пересечение А = М пЛГ; А={а / а еМ л а еЩ «п» - пересечение. «л» - обозначает букву «и». л (и) - логическая операция задается таблицей истинности (см. табл.3). Таблица 3
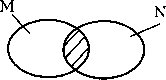 А=М nN Разность множеств А = М\ Ы,А={а/аеМлаеЫ} «\» - разность. «л» - обозначает букву «и». 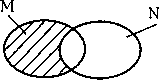 А = М \ N Подмножества М с N - «М» является подмножеством «ДГ». а е М => а е N Декартовы произведения множества А = МхМ,А={а / а = т,п \ т е М, п eN} (см. рис.2.10). Примечание. Имеет значение порядок сомножителей. % П2 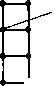 <т, п> <тл,н3> гщ т2 т3 тА т5 Рис.2.10. Изображение на решетке декартова произведения Примеры: R cz М х N, R - действительная прямая - множества точек прямой. R2 = 7? х R- плоскость, М х М = М - вторая степень декартова произведения, М х Мх...М = Мп - т-я степень декартова произведения, Ах В х С х Dx... - декартово произведение разных множеств. Логическое следствие МсЛГ, N czN о М =N Отношения R cz М х N - называется отношением на М, или m{Rmj о (mi ,mjeRczMxM. Отношением будем называть подмножество декартова произведения. Если два множества, то отношение - бинарное, если три - тернарное. В основном будем рассматривать бинарные отношения вида RczM2. R аМ\ я-арное произведение. R - (М, i?), R а М2, М - носитель отношения, R - сигнатура отношения. ?П(Г?П{находится в отношении «г» с элементом игу С понятием отношение тесно связано понятие - «граф» G а М х М. Графом G называется подмножество декартового произведения МхМ, то что изображено на решетке (см. рис.2.П.). Элементы множества М будем изображать «0», ти,- будем называть вершинами графа (рис.2.12.) Линия, соединяющая две вершины, называется дугой графа или ребром. т\ - т$ -> вершины графа. Отношение, или граф, носит также название структуры. 0 ... 43 44 45 46 47 48 49 ... 96 |












